17. Оценка статистической значимости уравнения в целом. F-критерий Фишера.

Поскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет место их разброс как обусловленный влиянием фактора х, т. е. регрессией у по х, так и вызванный действием прочих причин (необъясненная вариация). Пригодность линии регрессии для прогноза зависит от того, какая часть общей вариации признака у приходится на объясненную вариацию. Очевидно, что если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор х оказывает существенное воздействие на результат у. Это равносильно тому, что коэффициент детерминации R² будет приближаться к единице.

Любая сумма квадратов отклонений связана с числом степеней свободы (df— degrees of freedom), т. е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности N и с числом определяемых по ней констант. Применительно к исследуемой проблеме число степеней свободы должно показать, сколько независимых отклонений из N возможных требуется для образования данной суммы квадратов.

Так, для общей суммы квадратов требуется (n-1) независимых отклонений, ибо по совокупности из n единиц после расчета среднего уровня варьируют лишь (n - 1) число отклонений. При расчете факторной суммы квадратов - 1 степень свободы, и при расчете остаточной суммы квадратов - (n-2) степени свободы.

Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F – отношения (F - критерий):

    (8.1)

В качестве нулевой гипотезы Н₀выдвигается предположение о том, что линейной зависимости между x и y не существует.

Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Н₀ необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз.

Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы.

Табличное значение F-критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F -отношения признается достоверным (отличным от единицы), если оно больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи.

Если же величина окажется меньше табличной, то вероятность нулевой гипотезы выше заданного уровня (например, 0,05) и она не может быть отклонена, без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым, Н₀ не отклоняется.

18. Модель множественной регрессии.

Множественная регрессия – уравнение связи с несколькими независимыми переменными:

где - зависимая переменная (результативный признак);

- независимые переменные (факторы).

Линейная модель множественной регрессии имеет вид:

Y_i = α₀ + α₁x_i1 + α₂x_i2 + ... + α _mx_im + ε_i (4.1)

Коэффициент регрессии α_j показывает, на какую величину в среднем изменится результативный признак Y, если переменную x_j увеличить на единицу измерения, т.е. α_j является нормативным коэффициентом. Обычно предполагается, что случайная величина ε_i имеет нормальный закон распределения с математическим ожиданием равным нулю и с дисперсией σ².

Анализ уравнения (4.1) и методика определения параметров становятся более наглядными, а расчетные процедуры существенно упрощаются, если воспользоваться матричной формой записи уравнения (4.2):

Y = X α + ε (4.2)

где Y — вектор зависимой переменной размерности n×1, представляющий собой n наблюдений значений y_j,

X — матрица n наблюдений независимых переменных Х₁, Х₂, Х₃, ..., Х_m, размерность матрицы X равна n×(m+1);

α — подлежащий оцениванию вектор неизвестных параметров размерности (m+1) ×1;

ε — вектор случайных отклонений (возмущений) размерности n×1.

Таким образом,

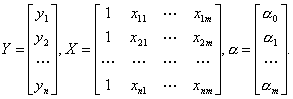
Уравнение (4.1) содержит значения неизвестных параметров α₀, α₁, α₂, ..., α_m. Эти величины оцениваются на основе выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки. Модель линейной регрессии, в которой вместо истинных значений параметров подставлены их оценки (а именно такие регрессии и применяются на практике), имеет вид:

, (4.3)

где α — вектор оценок параметров; е — вектор «оцененных» отклонений регрессии, остатки регрессии ε = Y - X α; — оценка значений Y, равная Ха.

Для построения уравнения множественной регрессии чаще используются следующие функции:

линейная –

степенная –

экспонента –

гипербола - .

Можно использовать и другие функции, приводимые к линейному виду.