2.2. Анализ применимости кратковременного преобразования Фурье.
Достоинства кратковременного преобразования Фурье очевидны. Для локально-стационарных сигналов результат, доставляемый с его помощью представляется хорошей основой для анализа.
Однако у кратковременного преобразования Фурье наличествует очевидный недостаток, происходящий от небезызвестного принципа Гейзенберга. Принцип, изначально применяемый к импульсам и положению элементарных частиц, может быть также применим к частотно-временным преобразованиям. Рассмотрим его более подробно.
2.3. Принцип Гейзенберга.
В оригинале принцип Гейзенберга гласит, что импульс и положения элементарной частицы не могут быть определены с исчерпывающей точностью одновременно. Математически этот принцип записывается так:
Et > 1
Аналогичное соотношение может быть получено и для преобразования Фурье. Положим
f 2= ( f2G(f)df)/ (G(f)df),
где G - преобразование Фурье сигнала g.
Величина f называется шириной спектра сигнала g .
Аналогично положим
t 2= ( t2g(t)dt)/ (g(t)dt).
Величина t называется разбросом времени сигнала.
Смысл вышеприведенных величин следующий - каждая из них показывает насколько данная функция (сигнал или его спектр) "размазан" вдоль соответствующей оси.
Принцип Гейзенберга для преобразования Фурье может быть записан следующим образом:
ft > 1.
Таким образом, если сигнал узко локализован во времени, то его спектр, напротив, рассредоточен по всей оси частот, и наоборот. Именно это свойство обуславливает основные ограничения применимости кратковременного преобразования Фурье.
Действительно, если с целью локализации сигнала во времени мы выберем достаточно "узкое" окно , то, согласно принципу Гейзенберга, мы получим достаточно значительную неопределенность по частоте. Если же, напротив, мы выберем достаточно "широкое" окно, то, согласно тому же принципу, возрастет неопределенность во времени.
Все вышесказанное иллюстрируется следующими примерами:
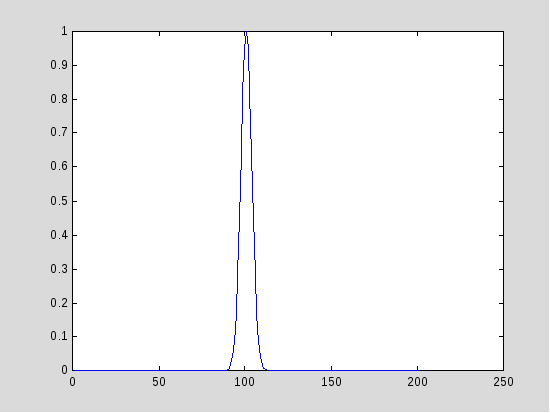
Рассмотрим функции окна, приведенные ниже.
|
a=0.1 |
a=0.001 |
Рис.5. Оконные функции для различных параметров a.
Все они являются частным случаем гауссовской функции окна, имеющей вид
w(t)=exp(-a*((t-b)^2)/2),
здесь a определяет ширину окна, b-положение, а t - время.
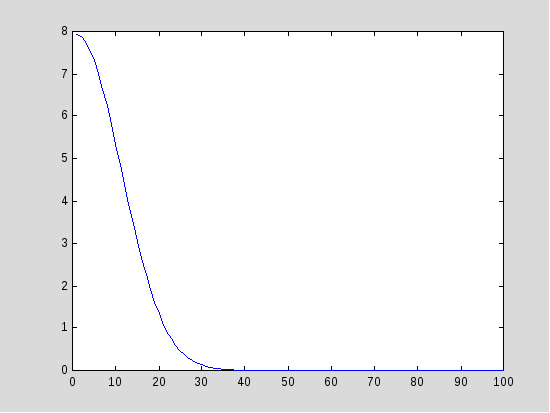
Рассмотрим спектр этих окон :
|
a=0.1 |
a=0.001 |
Рис.6. Спектры оконных функций для различных значений параметра а, (по горизонтальной оси отложена частота).
Из графиков видно, что если окно имеет хорошее разрешение во временной области, то оно имеет плохое разрешение в частотной и наоборот.
Проблемы применимости STFT, описанные выше, называются также проблемами разрешения.
Основная идея состоит в том, что разрешения по оси времени и частоты является величиной постоянной для всего преобразования.
Именно поэтому очевидным выходом из ситуации могут стать преобразования с переменным разрешением, такие как wavelet- преобразования, описанные ниже.
3. Непрерывное wavelet-преобразование и анализ со многими разрешениями.
3.1.Общие сведения
Несмотря на то, что проблемы разрешения по времени и частоте являются результатом физического явления (принцип неопределенности Гейзенберга wt>const ) и существуют независимо от используемого преобразования, есть возможность анализировать любой сигнал, используя альтернативный подход - анализ со многими разрешениями (Multiresolutional Analilysis -MRA ).
MRA, как видно из названия, дает возможность анализировать сигнал на различных частотах с разным разрешением. Разрешение для различных компонент спектра не одинаково, как это было в случае STFT . С помощью MRA можно получить хорошее разрешение по времени и плохое разрешение по частоте в области высоких частот и хорошее разрешение по частоте и плохое разрешение по времени в области низких частот. Этот подход имеет смысл, особенно когда компоненты сигнала с высокой частотой имеют небольшую длительность, а низкочастотные компоненты - достаточно большую. К счастью, сигналы, встречающиеся в практических приложениях, чаще всего имеют именно такую структуру.
Одним из наиболее популярных методов проведения анализа типа MRA является, так называемое WAVELET - преобразование.