
- •Тема: Предмет теории вероятностей (тв), ее значение для экономической науки. Случайные события. Алгебра событий.
- •§ 1. Элементы комбинаторики.
- •§ 2. Предмет теории вероятностей.
- •§ 3. Краткая историческая справка.
- •§ 4. Виды случайных событий.
- •§ 5. Классическое определение вероятности.
- •§ 6. Относительная частота. Статистическая вероятность.
- •Тема 2. Теоремы сложения и умножения вероятностей.
- •§1. Теорема сложения вероятностей несовместных событий.
- •§ 2. Полная группа событий.
- •§ 3. Теорема умножения вероятностей.
- •§ 4. Независимые события. Теорема умножения независимых событий.
- •§ 5. Вероятность появления хотя бы одного события.
- •§ 6. Теорема сложения вероятностей совместных событий.
- •§ 7. Формула полной вероятности.
- •§ 8. Формула Бейеса.
- •Тема: Повторение испытаний. Формула Бернулли.
- •§ 1. Формула Бернулли.
- •§ 2. Локальная теорема Лапласа.
- •§ 3. Интегральная теорема Лапласа.
- •Тема: Случайные величины.
- •§ 1. Дискретные и непрерывные случайные величины (св).
- •§ 2. Законы распределения вероятностей дсв.
- •§ 3. Числовые характеристики дискретных случайных величин.
- •§ 4. Дисперсия дискретной случайной величины.
- •Тема: Закон больших чисел (самостоятельно).
- •§ 1. Неравенство Чебышева. (рассмотреть самостоятельно)
- •§ 2. Теорема Чебышева.
- •Тема. Функция распределения вероятностей св.
- •§ 1. Функция распределения и ее свойства.
- •§ 2. График функции распределения.
- •§ 3. Плотность распределения вероятностей нсв.
- •Свойства плотности распределения.
- •§ 4. Законы распределения вероятностей.
- •§ 5. Нормальное распределение. Числовые характеристики нсв.
- •§ 6. Вычисление вероятности заданного отклонения
Тема: Закон больших чисел (самостоятельно).
§ 1. Неравенство Чебышева. (рассмотреть самостоятельно)
§ 2. Теорема Чебышева.
Теорема. Если
![]() попарно независимые случайные величины,
причем дисперсии их равномерно ограничены
(не превышают постоянного числа С),
то как бы мало ни было положительное
число ε,
вероятность неравенства:
попарно независимые случайные величины,
причем дисперсии их равномерно ограничены
(не превышают постоянного числа С),
то как бы мало ни было положительное
число ε,
вероятность неравенства:
![]() ,
,
будет сколько угодно близка к единице, если число случайных величин достаточно велико.
Это означает, что:
![]()
Если
![]() попарно-независимые СВ, имеющие одно и
тоже математическое ожидание а,
и если дисперсии этих величин равномерно
ограничены, то как бы мало ни было
попарно-независимые СВ, имеющие одно и
тоже математическое ожидание а,
и если дисперсии этих величин равномерно
ограничены, то как бы мало ни было
![]() ,
вероятность неравенства
,
вероятность неравенства
![]() будем как угодно
близка к единице, если число случайных
величин достаточно велико. Т.о. в условиях
теоремы справедливо равенство.
будем как угодно
близка к единице, если число случайных
величин достаточно велико. Т.о. в условиях
теоремы справедливо равенство.
![]() .
.
Теорема Чебышева справедлива не только для ДСВ, но и для НСВ.
Сущность теоремы
Чебышева в следующем. Хотя отдельные
независимые случайные величины могут
принимать значения далекие от своих
математических ожиданий, среднее
арифметическое достаточно большого
числа случайных величин с большой
вероятностью принимает значения близкие
к определенному постоянному числу:
![]() (или к числу а).
это означает, что отдельные случайные
величины могут иметь большой разброс,
а их среднее арифметическое рассеяно
мало.
(или к числу а).
это означает, что отдельные случайные
величины могут иметь большой разброс,
а их среднее арифметическое рассеяно
мало.
Нельзя уверено предсказать, какое возможное значение примет каждая из случайны величин, но можно предвидеть какое значение примет их среднее арифметическое. Это означает, что среднее арифметическое достаточно большого числа независимых случайных величин, дисперсии которых ограничены, утрачивает характер случайной величины. Это объясняется тем, что отклонения каждой из величин от своих математических ожиданий могут быть как положительными, так и отрицательными, а в среднем арифметическом они взаимно погашаются.
Теорема Чебышева имеет большое значение для практики. На этой теореме основан выборочный метод. Его суть в следующем. По сравнительно небольшой случайной выборке судят о всей совокупности (генеральной совокупности) исследуемых объектов.
Примеры: качество зерна, качество хлопка (оценивается по малой выборке из общего количества).
Теорема Бернулли. Если в каждом из n независимых испытаний вероятность p появления события А постоянная, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико:
![]() .
.
Тема. Функция распределения вероятностей св.
§ 1. Функция распределения и ее свойства.
ДСВ может быть задана перечнем всех ее возможных значений и их вероятностей. Для НСВ этот способ неприменим.
Действительно, рассмотрим случайную величину Х, возможные значения которой сплошь заполняют интервал (a,b). Очевидно, что в этом случае нельзя составить перечень всех возможных значений Х. Поэтому необходимо дать общий способ задания любых типов случайных величин. С этой целью вводятся функции распределения вероятностей случайных величин.
Пусть х – действительное число. Вероятность события, состоящего в том, что Х примет значение меньшее х, т.е. вероятность события Х < x обозначим F(x), где F(x) есть функция от х.
Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение меньше чем х, т.е. F(x) = P(Х < x).
Геометрически это означает, что F(x) есть вероятность того, что случайная величина Х примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
Определение. Случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
Рассмотрим свойства функции распределения.
Свойство
1. Значения
функции распределения принадлежат
отрезку [0;1]:
![]() .
.
Свойство
2. F(x)
– неубывающая функция, т.е.
![]() ,
если
,
если
![]() .
Из этого свойства следующие следствия.
.
Из этого свойства следующие следствия.
Следствие
1. Вероятность
того, что случайная величина примет
значение, заключенное в интервале (a,b)
равна приращению функции распределения
на этом интервале:
![]() .
.
Пример. Случайная величина Х задана функцией распределения:
![]()
Найти вероятность того, что в результате испытания случайная величина Х примет значение, принадлежащее интервалу (0,2):
P(0 < X < 2) = F(2) – F(0).
Решение. На интервале (0,2) по условию
![]() ,
тогда
,
тогда
![]() ;
;
![]() .
.
Следствие 2. Вероятность того, что непрерывная случайная величина примет одно определенное значение равна нулю.
Свойство 3. Если возможные значения случайной величины принадлежат интервалу (a,b), то:
F(x) = 0 при
 ;
;F(x) = 1 при
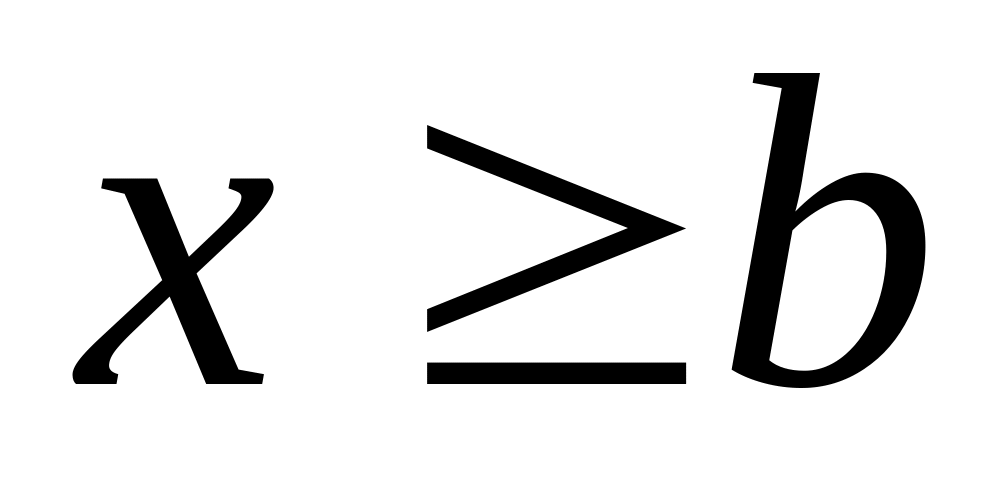 .
.
Следствие.
Если возможные значения НСВ расположены
на всей оси х, то:
![]() .
.
