§ 5. Нормальное распределение. Числовые характеристики нсв.
Определение 1.
Математическим ожиданием НСВ Х,
возможные значения которой принадлежат
отрезку
,
называют определенный интеграл:
.
Если возможные значения принадлежат всей оси Ox, то
.
Предполагается,
что несобственный интеграл сходится
абсолютно, т.е. существует
.
Определение 2. Дисперсией НСВ, называют математическое ожидание ее отклонения:
.
Среднее квадратичное
отклонение:
(также
для ДСВ).
Определение 3. Нормальным называют распределение вероятностей НСВ, которое описывается плотностью:
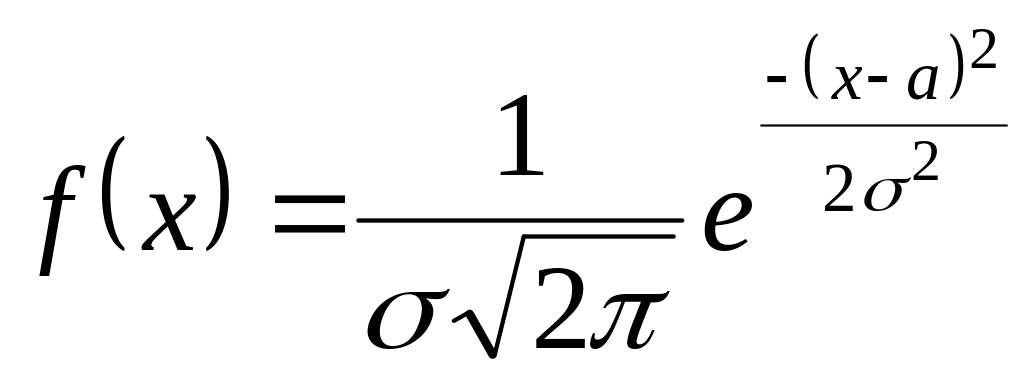
Нормальное распределение определяется двумя параметрами: а и σ, где
а – математическое ожидание;
σ – среднее квадратическое отклонение.
График плотности нормального распределения называют нормальной кривой или кривой Гаусса.
Исследуем функцию:
.
Очевидно, что функция определена на всей числовой оси.
При всех значениях x функция принимает положительные значения, т.е. нормальная кривая расположена над осью OX.
Предел функции при неограниченном возрастания
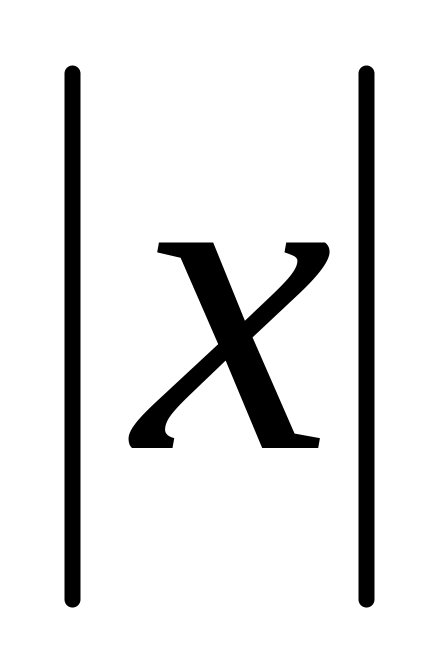равен нулю:
,
т.е. ось ОХ
является горизонтальной асимптотой
графика.Исследуем функцию на экстремум найдем:
;
.
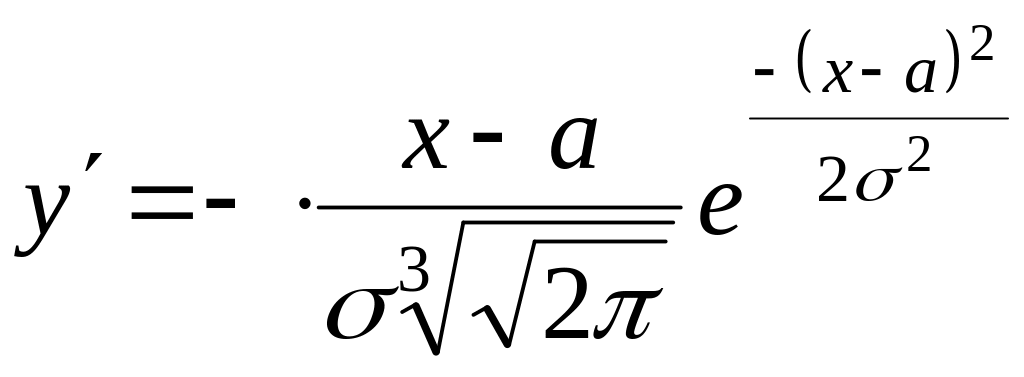Если
,
;
если
,
то
;
если
,
то
.
Следовательно при
функция имеет максимум:
.
График функции симметричен относительно прямой .
Найдем точки перегиба функции. Найдем
.
;
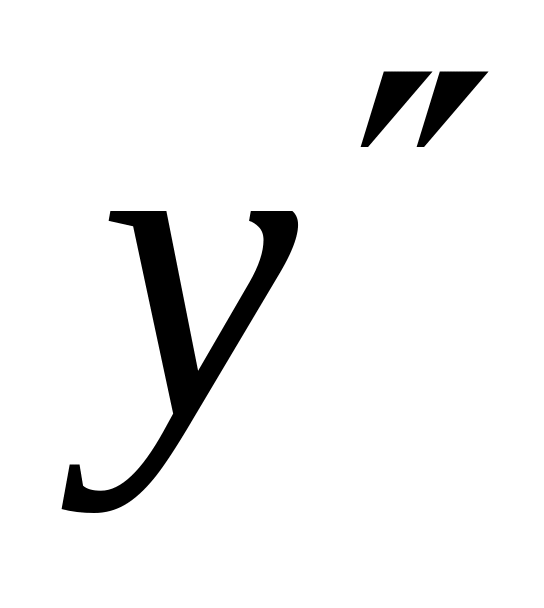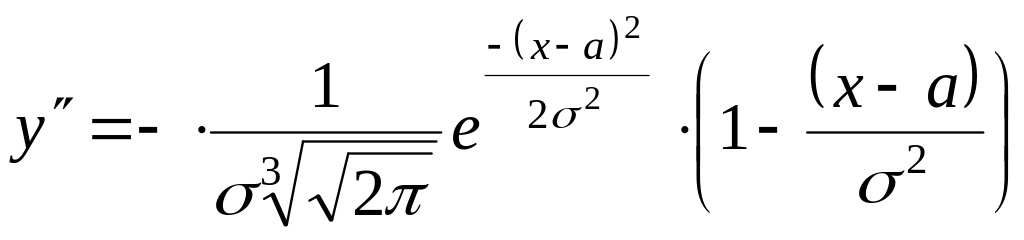Показать
самостоятельно, что при
и
вторая производная
и при переходе через эти точки она меняет
знак; и точки
;
- являются точками перегиба. При
и
график нормальной кривой имеет вид:
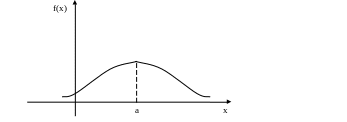
Изменение величины параметра а (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси ОХ, вправо, если, а возрастает и влево, если убывает.
Можно показать,
что с возрастанием
ордината
нормальной кривой убывает, кривая
становится пологой, т.е. сжимается к оси
ОХ;
при убывании
нормальная кривая становится равной
1.
Графики имеют такой вид:
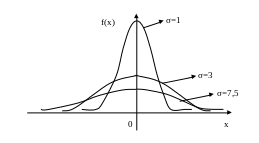
Пусть случайная величина Х распределена по нормальному закону. Тогда вероятность того, что случайная величина Х примет значение, принадлежащее интервалу (α,β) равна:
.
Преобразуем эту формулу так, чтобы можно было пользоваться функцией Лапласа, и получим формулу:
(*)
Пример. Случайная величина распределена по нормальному закону. Математическое ожидание а = 30, среднее квадратическое отклонение σ = 10. Найти вероятность того, что Х примет значение, принадлежащее интервалу (10, 50).
Решение. α = 10, β = 50, а = 30, σ = 10.
По формуле (*):
По таблице находим:
=
0,4772
§ 6. Вычисление вероятности заданного отклонения
Часто требуется
вычислить вероятность того, что отклонение
нормально распределенной случайной
величины Х по абсолютной величине меньше
заданного положительного числа δ,
т.е. требуется найти вероятность
осуществления неравенства.
.
Используя формулу Лапласа, получим:
(**)
Пример. Случайная величина Х распределена нормально. Математическое ожидание и среднее квадратическое отклонение Х соответственно равны: а = 20, σ = 10. найти вероятность того, что отклонение по абсолютной величине будет меньше трех.
Решение. Применим формулу:
а = 20, σ = 10, δ = 3.
.
По таблице находим: Ф(0,3) = 0,1179.
.
Преобразуем формулу (**).
Пусть δ
= σt,
если t
=3, получим
δ
= 3σ.
Тогда
.
Это означает, что вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения равна 0,9973 и вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение очень мала, а именно равна 0,0027%. Это означает, что только в 0,27% случаев так произойдет. Такое правило называется правилом трех сигм.