2. Неперервність ф-ї багатьох змінних.

Означення: нехай ф-я z=f(x,y)=f(М) визначена на деякій множині D, точка М₀D і довільний -окіл точки М₀ містить точки множини D, ф-я z=f(М) називається неперервною, якщо (1).

Означення: точки, в яких ф-я неперервна, називаються точками неперервності ф-ї, а точки в яких неперервність порушується називаються точками розриву ф-ї.

(кроме 1 і 2). Точка (1,2) є точкою розриву ф-ї, оскільки 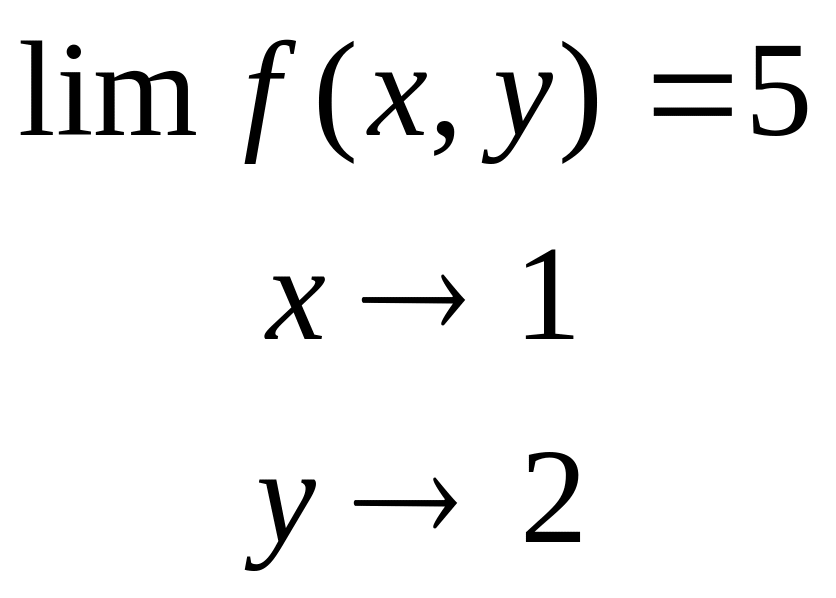, f(1,2)=1.

В умові (1) неперервності ф-ї можна надати іншого вигляду. Позначимо через х=х-х₀, у=у-у₀, z=f(x,y)-f(x₀,y₀). Величини х і у називають приростами аргумента, а величину z повним приростом ф-ї f(x,y) в т. М₀(х₀, у₀)з (1) сліду., що або (2) таким чином рівність (2) дає ще одне рівносильне озн-я непер-ті ф-ї.

1*)Оз-я: Нехай ф-я z=f(М) визначена на D і точка M₀D і довільне О_М₀ містить т. множ Р , ф-я z=f(м) наз-я неперервною в точці M₀ , якщо її повний приріст в цій точці прямує до 0 коли х, у прямують до 0.

Приклад: z= х²+у² неперервна в будь-якій точці М₀(х₀, у₀)R² z=(х₀+х)²+(у₀+у)²--(х₀²+у₀²)=2х₀х+х²+2у₀у+у²0 когда х0 і у0. Тобто .

Зауваження: Використовуючи означення неперервності ф-ї та границі ф-ї багатьох змінних можна довести, що арифметичні операції над неперервними ф-ями та побудова складної ф-ї з неперервної ф-ї багатьох змінних приводять до неперервних ф-й.

Означення: D R² називаються связною, якщо будь-які 2 точки даної множини можна сполучити неперервною лінією, яка цілком належить множині D.

Приклад: Якщо розглянути множину, що складається з 2 кругів, які не мають спільних точок, то дана множина не є связною.

Означення: Точка М – внутрішня точка D R², якщо _(М) який цілком належить D.

Означення: D R² – відкрита, якщо кожна її точка – внутрішня.

Приклад: х²+у²1 – відкрита множина.

Означення: Областю (або відкритою областю) називають связну відкриту в R² множину.

Приклад: х²+у²1 – відкрита область в R².

Означення: Точка МD – межовою точкою множини, якщо кожен окіл точки М містить точки які належать D так і точки, які D не належать.

Множина всіх межових точок утворює межу області D.

Приклад: Для множини х²+у²1 межею є лінія х²+у²=1.

Означення: Область разом з її межею називають замкненою областю.

Означення: Область обмежена, якщо вона цілком міститься у деякому крузі скінченого радіуса.

Приклад: необмежена связна множина яка не має внутрішніх точок в R².

Сформулюємо властивості неперервних ф-й багатьох змінних (2 змінних) заданих в замкнений обмеженій області.

Зауваження: Замкнена обмежена область для ф-ї 2 змінних є аналогом відрізка для ф-ї 1 змінної, тому властивості аналогічні властивостям неперервної на відрізку ф-ї 1 змінної.

Теорема 1: z=f(М), задана у замкненій обмеженій області, обмежена у цій області.

Теорема 2: Неперервна z=f(М), задана у замкненій обмеженій області D R² набуває в області D найбільшого і найменьшого значення.

Теорема 3: Нехай ф-я z=f(М) неперервна в замкненій обмеженій області D, що  R² і, якщо

f(М₁) f(М₂), де М₁ і М₂ D, то іспользуя т. M₀D, така що f(М₀)=, зокрема, якщо f(М₁)0, а f(М₂)0, іспользуя т. M₀D така, що D, f(М₀)=0.