6. Екстремум ф-ї 2 змінних. Необхідні і достатні умови.

Нехай z=f(x,y) визначена в області DR², а т. М₀(х₀, у₀)єD.

Означення: Якщо існує такий окіл т. М₀ який цілком належить області D для всіх точок М якого відмінних від М₀ виконується нерівність f(М) f(М₀), то точка М₀ називається локальним мінімумом ф-ї z.

Означення: Якщо існує такий окіл т. М₀ який цілком належить області D для всіх точок М якого відмінних від М₀ виконується нерівність f(М)f(М₀), то точка М₀ називається локальним максимумом ф-ї z.

Точки локального максимума і мінімума називаються точками екстремума ф-ї.

Теорема 1(необхідні умови екстремума): Якщо ф-я z=f(x,y) має в т. М₀(х₀, у₀) локальний екстремум, то в цій точці похідні 1 порядку по змінним х, у або =0 або не існує.

Доведення: Нехай т. М₀ – локальний екстремум ф-ї f(x,y). Розглянемо ф-ю f(x,y₀). Тоді за теоремою про необхідні умови екстремума ф-ї f’(x₀,y₀)=0 або не існує. Аналогічно розглядаємо ф-ю f(x,y₀) одержимо, що f_у’(x₀,y₀)=0 або не існує.

Зауваження: Подібна теорема справедлива і для ф-ї n змінних.

М₀(х₀, у₀) де f_х’_М0= f_у’_М0 =0 – стаціонарна точка. Стаціонарна точки, а також точки в яких похідна не існує – критичні точки. Таким чином, якщо ф-я у якій небудь точці має локальний екстремум, то цуя точка є критичною. Обернене твердження не виконується.

Теорема (достатні умови екстремума): Нехай в стаціонарній точці М₀(х₀, у₀) і деякому її околі ф-я f(x,y) має неперервні частинні похідні 2 порядку і величина (х₀, у₀)=f_хх^”(х₀, у₀). (х₀, у₀)=f_хх^”(х₀, у₀)f_уу^”(х₀, у₀)-f_ху^”(х₀, у₀)²0, то f(x,y) має в точці М₀ локальний екстремум, причому, якщо f_хх^”(х₀, у₀)0, то т. М₀ – точка локального мінімума f(х,у), а якщо f_хх^”(х₀, у₀)0, то т. М₀ – точка локального максимума f(х,у).

У випадку коли (х₀, у₀)0 f(х,у) не має в точці М₀ локального екстремума.

Приклад: Знайти екстремум ф-ї z=x²+xy+y²-3x-6y.

f_x’=2x+y-3=0. f_y’=x+2y-6=0. x=0,y=3. Знайдемо значення часних похідних 2 порядку у цій точці: f_хх^”_М=2, f_уу^”_М=2, f_ху^”_М=1. (0,3)=f_хх^”_Мf_уу^”_Мf_ху^”_М-f_ху^”_М²=30. min f(x,y)=f(0,3)=9-18=-9.

Теорема 3 (2 достатня умова існування екстремума): Якщо М₀(х₀, у₀) – стаціонарна точка ф-ї z=f(х,у) і d²f(M₀), то точка М₀ точка локального мінімума, якщо менше 0, то локального максимума.

Умовний екстремум ф-ї 2 змінних.

Нехай в області DR² визначена z=f(x,y) і рівнянням (x,y)=0 задана деяка крива L в заданій області. Задача полягає в тому, щоб на L знайти т. М(х,у) у якій z=f(x,y) набуває найбільшого (найменшого) значення у порівнянні з іншими точками кривої L. Така точка М(x,y) називається точкою умовного екстремуму ф-ї f(x,y) на кривій L. Зазначимо, що на відміну від звичайного екстремуму знаходження ф-ї в т. умовного екстремуму порівнюється із значенням цієї ф-ї не в усіх точках області D, а лише із значеннями ф-ї на L.

Назва умов екстремуму пов’язана з тим, що змінні х та у мають додаткову умову (x,y)=0. Це рівняння називають також рівнянням зв’язку. Якщо це рівняння можна розв’язати відносно однієї з змінних (наприклад у=(х)), то підставляють замість у у ф-ю z=f(x,y) (х), одержимо ф-ю 1 змінної z=f(x,(х)). Оскільки додаткова умова врахована, то цю ф-ю, щоб дослідити на умовний екстремум необхідно дослідити на дослідження звичайного екстремума ф-ї 1 змінної. Однак у загальному випадку (x,y)=0 не завжди можна розв’язати відносно х або у. Тоді це рівняння розглядають як рівняння, що визначає у, як наявну ф-ю від х.

Продиференціюємо його по х: 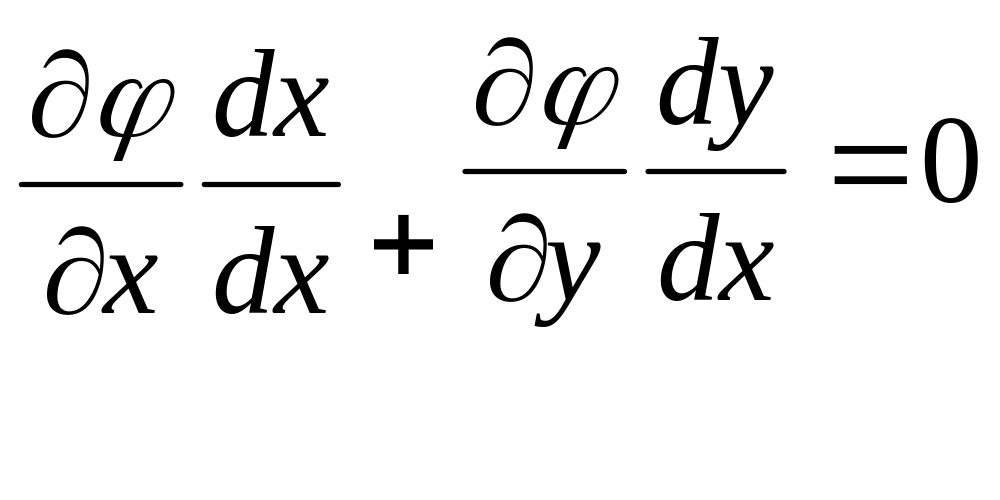, dy/dx=-_x’/_y’ (1). Розглянемо z=f(x,y) як складену ф-ю. З необхідністю умови екстремуму випливає, що у точка екстремуму dz/dx=(z/x)(dx/x)+(z/y)(dy/dx)=0 (2). Підставимо в (2) (1), одержимо: f_x’(z/x)+f_y’(z/y)(-_x’/_y’)=0; z/x=z_x’=f_x’; f_x’/_x’=f_y’/_y’=-. Тоді f_x’+ f_x’=0, f_y’+f_y’=0. Таким чином стаціонарна точка умовного екстремуму повинна задовольняти рівнянню.

((x,y)=0, (f/x)+(/x)=0, (f/у)+(/у)=0) (3). Аналізуючи систему бачимо, що задача знаходження умовного екстремуму звелася до задачі знаходження екстремуму ф-ї F(x,y)=f(x,y)+ (x,y) (4) – ф-я Лагранжа, а  - множник Лагранжа. Умови (3) є лише необхідними. Вони дають змогу знайти стаціонарні точки умовного екстремуму з теореми 3 питання 8 характер умов екстремуму можна визначити за знаком диференціалу другого порядку у цій точці. Якщо d²F|_M0, т. M – min; d²F|_M0, т. M – mах.

Приклад: дослідити на умовний екстремум ф-ю z=x³+y³, x+y=0. F(x,y)=x³+y³+(x+y-z). (x+y=0, 3x²+=0, 3y²+=0)  (x+y=0, x²=y²)  (x+y=2, (x-y)(x+y)=0)  (x=1, y=1). Таким чином, М(1,1) – стаціонарна точка. d²F=bxdx²+bydy²  d²F|_M=bdx²+bdy². Таким чином в т. М ф-я z має min min z=1³+1³=2.