
- •1.Функція багатьох змінних. Границя функції багатьох змінних.
- •2. Неперервність ф-ї багатьох змінних.
- •3.Частинні похідні. Диференцируємость ф-ї багатьох змінних.
- •4.Повний диференціал ф-ї багатьох змінних. Диференціали вищих порядків.
- •5. Похідні складної ф-ї багатьох змінних. Диференціал складної ф-ї багатьох змінних.
- •6. Екстремум ф-ї 2 змінних. Необхідні і достатні умови.
- •7. Невласні інтеграли 1 роду. Приклади.
- •8. Невласні інтеграли 2-го роду.
- •9.Числові ряди Найпростіші властивості.
- •10.Ознаки порівняння додатніх числових рядів.Приклади.
- •11. Знакоочередні ряди. Ознака Лейбніца. Знакозмінні ряди. Абсолютна і умовна збіжності.
- •Теорема2(Абелья) Якщо ряд (1) розбіжний в точці то він буде розбіжним для всіх
- •14.Ряд Тейлора
- •14.2Разложение элементарн. Функций в ряд Макларена
- •15 Тригонометрический ряд Фурье.
8. Невласні інтеграли 2-го роду.
Нехай
ф-я f(x)
визначена на проміжку [a,b)
точку х=b
назвемо особливою якщо f(x)
коли х
b-0.
Нехай х=b
особлива точка ф-ї f(x)
і ця ф-я інтегрована на відрізку [a,b-)
де >0;
b->a.
Якщо існує скінченна границя коли
![]() (1) то її наз-ть невласним інтегралом
2-го роду. Якщо (1)=
або не існує то невласний інт-л наз-ся
розбіжним. У випадку коли х=a
особлива точка ф-ї
f(x)
невласний інтеграл 2-го роду визначається
рівністю:
(1) то її наз-ть невласним інтегралом
2-го роду. Якщо (1)=
або не існує то невласний інт-л наз-ся
розбіжним. У випадку коли х=a
особлива точка ф-ї
f(x)
невласний інтеграл 2-го роду визначається
рівністю:
![]() =
=![]()
![]() .
У випадку коли с0(a,b)
особлива т-а ф-ї
f(x)
то
.
У випадку коли с0(a,b)
особлива т-а ф-ї
f(x)
то
= +
+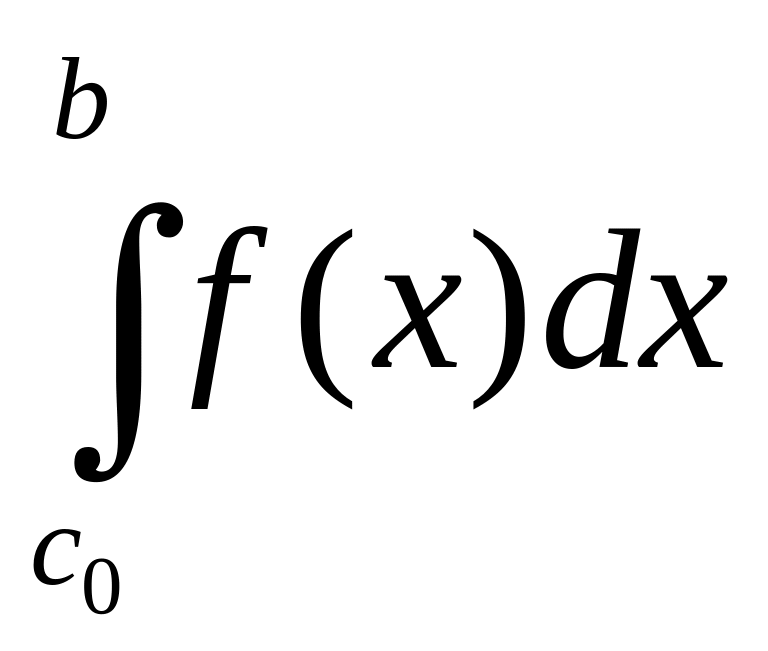 (2).
Інт-л (2) назвемо збіжним коли збіжні
будуть оба інт-ли у правій частині (2).
У випадку коли х=a
х=b
– особливі т ф-ї невласний інт-л
визначається рівністю:
(2).
Інт-л (2) назвемо збіжним коли збіжні
будуть оба інт-ли у правій частині (2).
У випадку коли х=a
х=b
– особливі т ф-ї невласний інт-л
визначається рівністю:
=![]() +
+![]() (3)
де с-будь яка точка с(a,b).
Інт-л (3) наз-мо збіжним якщо збіжні оба
інтеграли у правій частині (3) незалежно
від вибору точки а.
(3)
де с-будь яка точка с(a,b).
Інт-л (3) наз-мо збіжним якщо збіжні оба
інтеграли у правій частині (3) незалежно
від вибору точки а.
Приклад:
![]() , >0,
х=0-особлива точка 1/х.
1)=1
, >0,
х=0-особлива точка 1/х.
1)=1
![]() =
=

![]() (розбіжний).
(розбіжний).
1, >0 =




 =
= .
Таким чином
збігаються коли
і розбігаються коли 1.
.
Таким чином
збігаються коли
і розбігаються коли 1.
Теорема
1: Якщо ф-ї f(x)
і g(x)
неперервні на проміжку [a;b)
і мають особливу точку х =b
і задовольняють нерівності 0f(x)g(x),
xє[a;b),
то якщо
![]() -збігається,
то
збігається.
Якщо
розбіжний, то розбіжним буде
.
-збігається,
то
збігається.
Якщо
розбіжний, то розбіжним буде
.
Приклад:
Дослідити на збіжність інтеграл.
![]() (т.
х=0) на [0;1)
виконується нерівність: 1/(х1/2+5х4)
1/х1/2
оскільки
(т.
х=0) на [0;1)
виконується нерівність: 1/(х1/2+5х4)
1/х1/2
оскільки
![]() - збіжний, то
- збіжний, то
![]() - збіжний.
- збіжний.
Теорема
2: Якщо ф-ї f(x)
і g(x)
неперервні додатні на проміжку [a;b)
і мають особливість в точці х =b
і
![]() ,
то інтеграли
і
мають однакову поведінку, або одночасно
збігаються, або одночасно розбігаються.
,
то інтеграли
і
мають однакову поведінку, або одночасно
збігаються, або одночасно розбігаються.
11продолжПриклад:
![]() неперервні і додатні на [0;1)
мають особливість в точці х=0.
неперервні і додатні на [0;1)
мають особливість в точці х=0.
Розглянемо

 .
розбігається, то за теоремою 2
.
розбігається, то за теоремою 2
![]() - розбігається.
- розбігається.
Теорема
3: Якщо х=b
особлива точка f(x)
і
![]() збігається, то збігається і інтеграл
.
збігається, то збігається і інтеграл
.
Приклад:
![]() .
Підінтегральна ф-я знакозмінна і має
особливість в т. х=0. Розглянемо інтеграл
.
Підінтегральна ф-я знакозмінна і має
особливість в т. х=0. Розглянемо інтеграл
![]() .
.
![]()
![]() збіжний, тому, що ,
то за теоремою 1 збіжний
,
а за теоремою 3 збіжний
збіжний, тому, що ,
то за теоремою 1 збіжний
,
а за теоремою 3 збіжний
9.Числові ряди Найпростіші властивості.
О-я: Нехай задана посл-ть дійсних чисел {an}={a1,a2,…., an ….}.
Числовим
рядом наз-ся вираз a1,a2,….,
an
…=![]() .
.
Число an- енний член ряду.
Число Sn наз-ся частинною измою ряду (1).
Сумой ряду 1 наз-ть вел-у S=limn Sn.
Ряд 1 збіжний якщо його сума –скінченне число.
Якщо сума= або не існує то ряд 1 наз-ся розбіжним.
Властивості збіжних рядів:
1)Якщо - збіг-ся і має суму сS, де с- конят .
Дов-ня:
Нехай
Sn=![]() ,n=
,n=![]() =сSn.
=сSn.
limn Sn=S, limn n= limn сSn=сS.
2)Якщо
ряди
і
![]() збіг-ся і мають суми А і В то збіжн-ми
єтакож ряди
збіг-ся і мають суми А і В то збіжн-ми
єтакож ряди
![]() =А
=А![]() В.
В.
Дов-ня:
Нехай
Sn=
,
n=![]()
S*n=![]() ,
S*n=
Sn
n
,
S*n=
Sn
n
Тоді limn Sn=А , limn n=В.
3)Збіжність ряду не зміниться якщо до цього ряду приєднати або відкинути скінченну кіль кість членів.
Дов-я:
Нехай Sn- частинна сума ряду 1. сm- сума відкинутих членів, n- таке велике щоб всі відкинуті члени знаходились в Sn. n-m-сума членів ряду що містяться в Sn і не містяться у сm.
Тоді Sn= сm+n-m тоді limn Sn= сm+ limn n-n.
З 2 впливає що гр. І влівій і правій частинах одн-но існує або не існує тобто ряд один збіжний(розб-й) коли збіжн-й(розб-й) ряд m n-го членів.
О-я:
rn=![]() ,
вираз rn
наз-я n-им
залишком ряду 1. Тобто його можна
розглядати як суму ряду 1 без перших n
його членів.
,
вираз rn
наз-я n-им
залишком ряду 1. Тобто його можна
розглядати як суму ряду 1 без перших n
його членів.
4)Ряд 1 збіжн-й тоді і тільки тоді коли збіг-ся його залишок.
5)Необхідна умова збіжності .
Якщо 1 збіг-ся то limn аn=0.
Дов-ня:
За умовою S=limn Sn зрозуміло що S=limn Sn-1. Тоді limn аn= limn (Sn- Sn-1).
Достатня умова розбиття ряду:
Якщо limn аn0 то , дійсно як-би ряд був збіжним то за 5) його залежний член прямував би до 0 при n а це суперечить умові.
