
- •1.Функція багатьох змінних. Границя функції багатьох змінних.
- •2. Неперервність ф-ї багатьох змінних.
- •3.Частинні похідні. Диференцируємость ф-ї багатьох змінних.
- •4.Повний диференціал ф-ї багатьох змінних. Диференціали вищих порядків.
- •5. Похідні складної ф-ї багатьох змінних. Диференціал складної ф-ї багатьох змінних.
- •6. Екстремум ф-ї 2 змінних. Необхідні і достатні умови.
- •7. Невласні інтеграли 1 роду. Приклади.
- •8. Невласні інтеграли 2-го роду.
- •9.Числові ряди Найпростіші властивості.
- •10.Ознаки порівняння додатніх числових рядів.Приклади.
- •11. Знакоочередні ряди. Ознака Лейбніца. Знакозмінні ряди. Абсолютна і умовна збіжності.
- •Теорема2(Абелья) Якщо ряд (1) розбіжний в точці то він буде розбіжним для всіх
- •14.Ряд Тейлора
- •14.2Разложение элементарн. Функций в ряд Макларена
- •15 Тригонометрический ряд Фурье.
7. Невласні інтеграли 1 роду. Приклади.
Нехай f(x) визначена на [a;+] , де 0аb, якщо існує скінчена границя
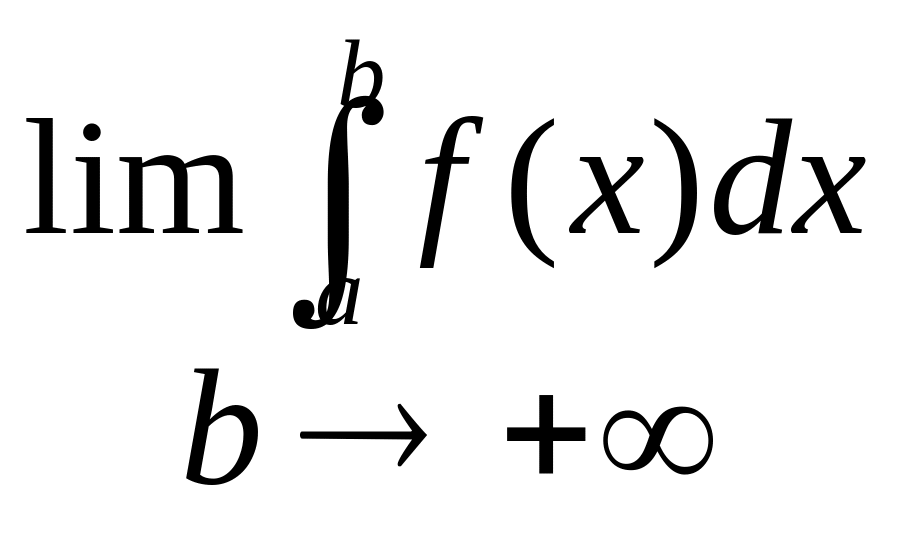
, то цю
границю називають невласним інтегралом
1 роду і позначають
![]() (1).
(1).
У цьому випадку інтеграл (1) називається збіжним, а ф-я f(x) інтегров. на [а;+ ].
Якщо вказана границя не існує або є , то інтеграл (1) розбіжний, а ф-я f(x) неінтегров. на [а;+ ].
Аналогічно
визначається
![]() =
=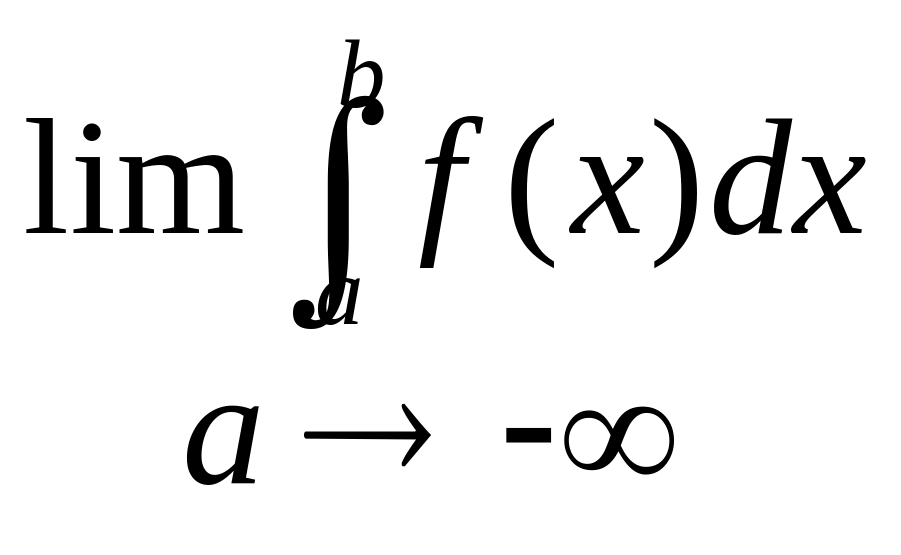 .
.
Невласний
інтеграл з двума нескінченими межами
визначається рівностями (2)
![]() =
=![]() +
+![]() ,
с-довільне число.
збіжний коли є збіжним обидва інтеграла
справа. Можна довести, що інше визначення
(2) не залежить від вибору с.
,
с-довільне число.
збіжний коли є збіжним обидва інтеграла
справа. Можна довести, що інше визначення
(2) не залежить від вибору с.
Зауваження: З означення невласних інтегралів випливає невласні інтеграли є проп-ю інтегральних сум, а є границя визначеного інтегралу із змінною межею інтегрування. І виражає площу необмеженої області.
Приклад:
Дослідження на збіжність.
![]() 1) =1
1) =1
![]() =
=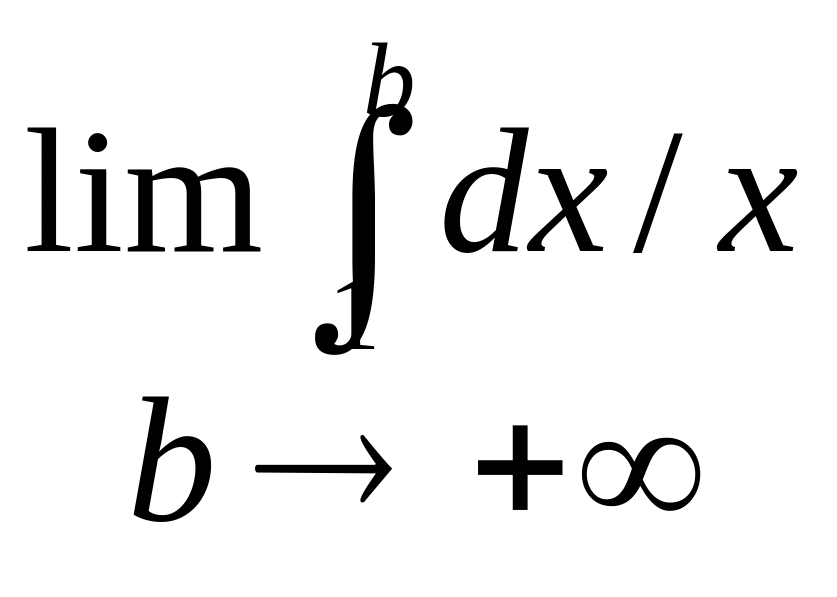 =
=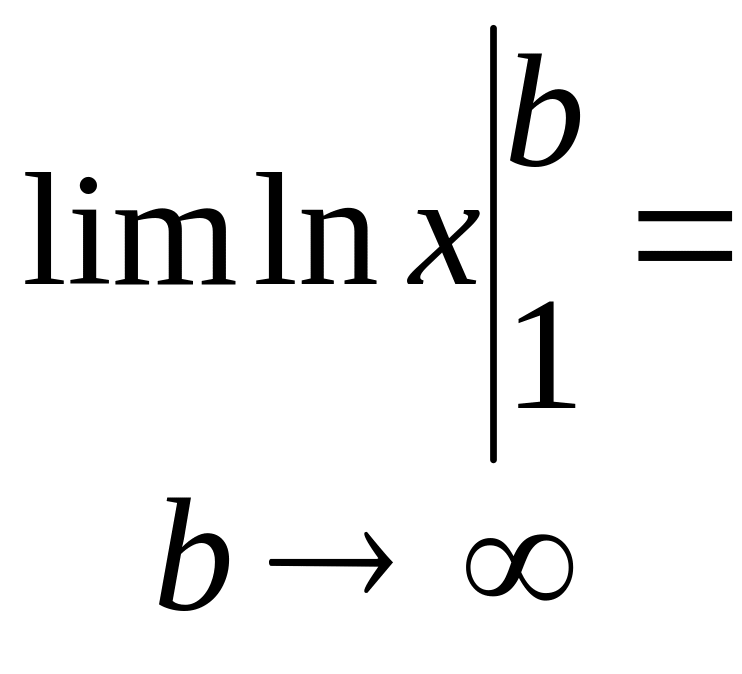
![]() =
інтеграл розбіжний. 2) 1
=
інтеграл розбіжний. 2) 1![]() =
=
![]()
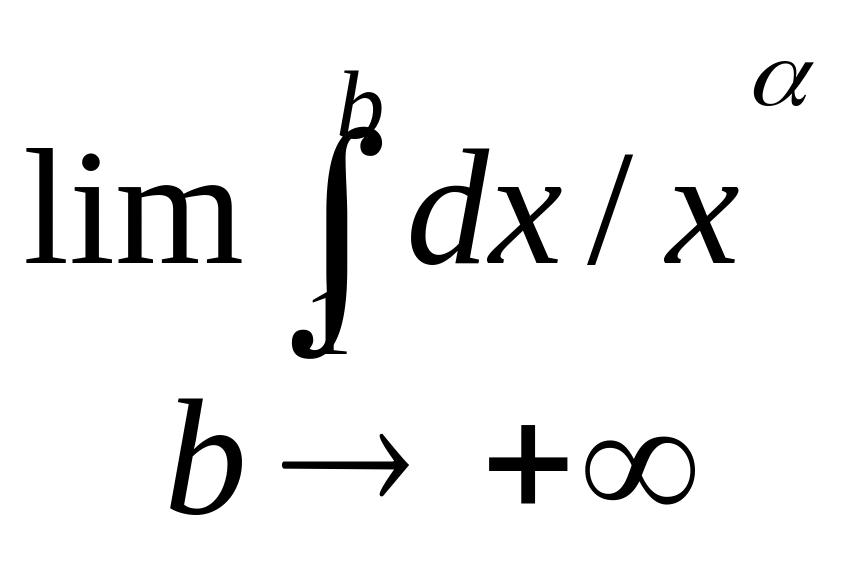 =
=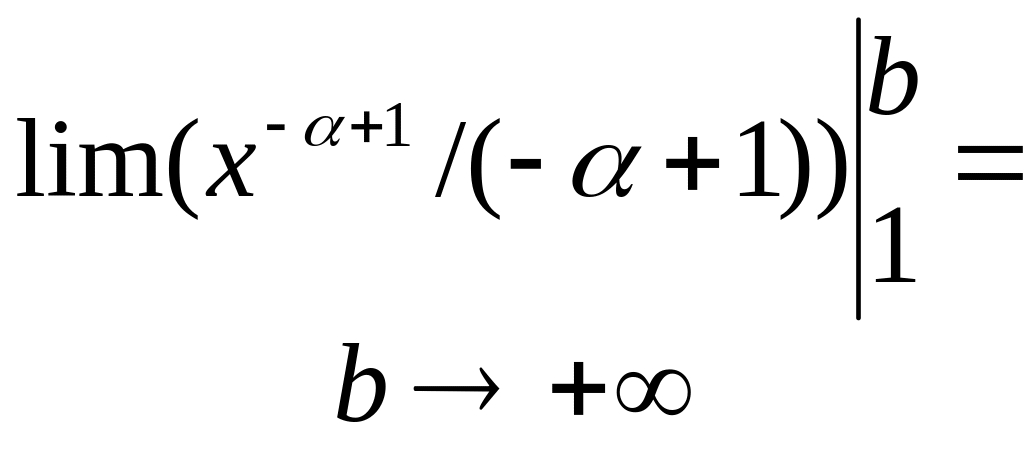
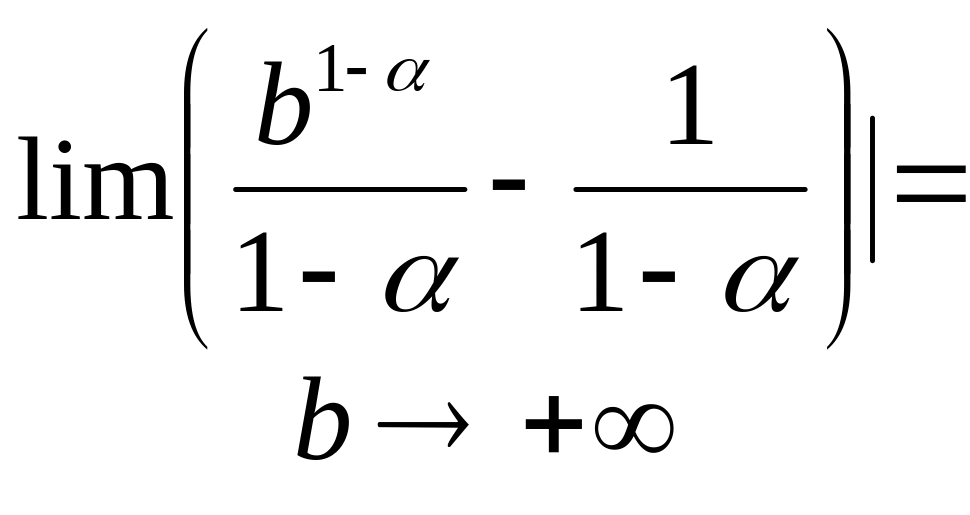
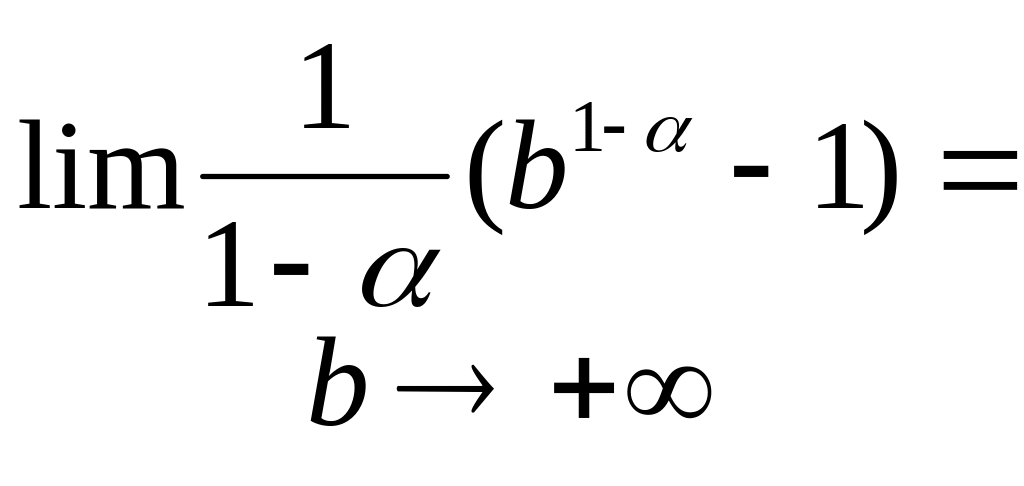
![]() .
.
Таким
чином інтеграл
збігається,
якщо
і розбігається коли 1.
Розглянемо деякі ознаки збіжності
невласних інтегралів. Нехай на [a,+)
ф-ї f(x)
і g(x)
неперервні і задовольняють нерівності
0f(x)g(x),
хє[a,+).
Тоді
![]() (3)
(3)
![]() (4).
З(3) випливає (4), а із розбіжності (4)
розбіжність (3).
(4).
З(3) випливає (4), а із розбіжності (4)
розбіжність (3).
Якщо площа більшої за розмірами області – скінчене число і меншої – скінчене число і якщо менше за розмірами області нескінченно велика величина, то і більшої нескінченно велика величина.
Приклад:
Дослідити на збіжність інтеграл.![]() оскільки Оскільки
оскільки Оскільки
![]() збігається (дивиться попередній
приклад), то за теоремою (1) збіжним є
також і
.
збігається (дивиться попередній
приклад), то за теоремою (1) збіжним є
також і
.
Теорема
2: Якщо ф-ї f(x)
і g(x)
неперервні визначені на інтервалі
[a,+)
і задовольняють
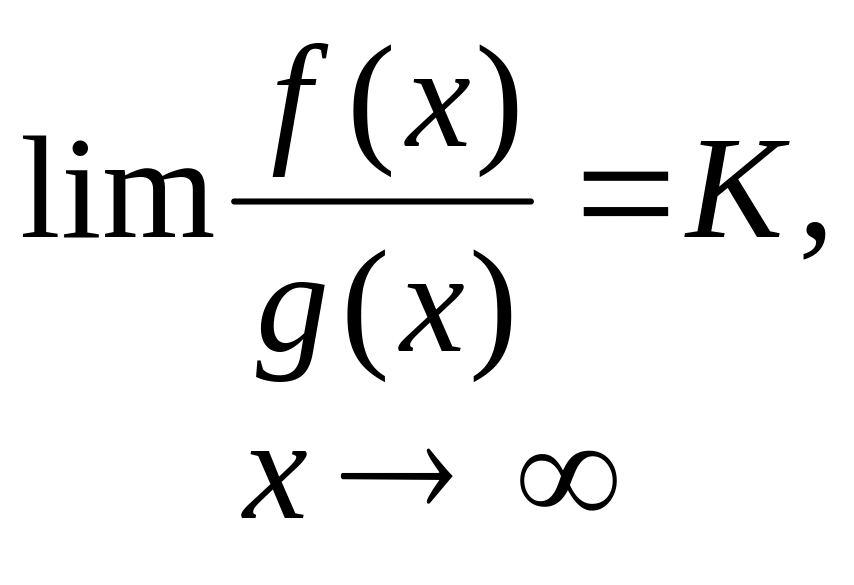 де (0К),
f(x)0
і g(x)0,
хє[a,+),
то інтеграли (3) і (4) або одночасно
збігаються або одночасно розбігаються.
де (0К),
f(x)0
і g(x)0,
хє[a,+),
то інтеграли (3) і (4) або одночасно
збігаються або одночасно розбігаються.
Приклад:
Дослідити на збіжність інтеграл.
![]() . Оскільки
збіжний
(дивиться попередній приклад
розглянемо
. Оскільки
збіжний
(дивиться попередній приклад
розглянемо
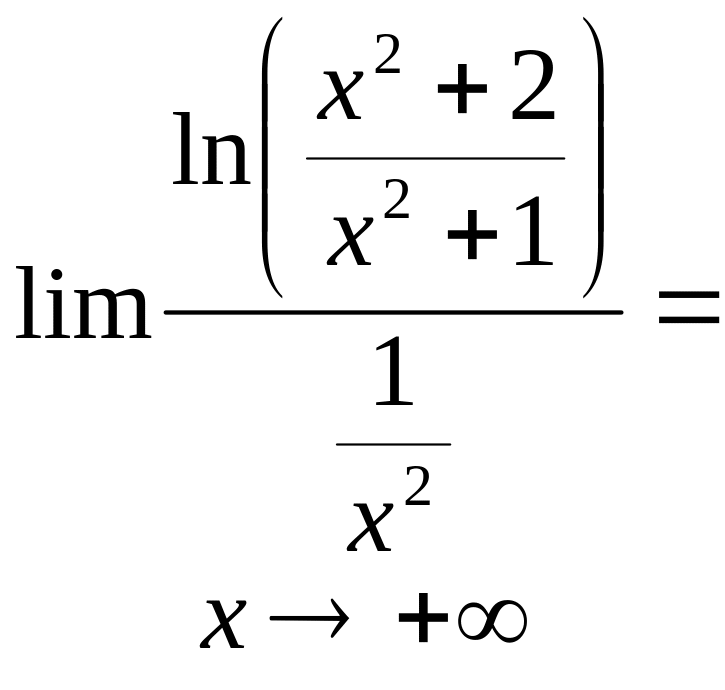
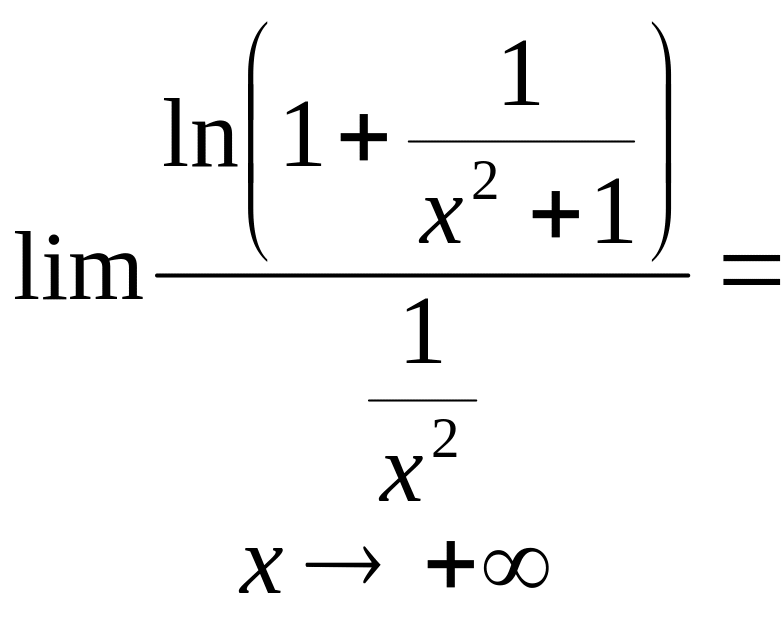
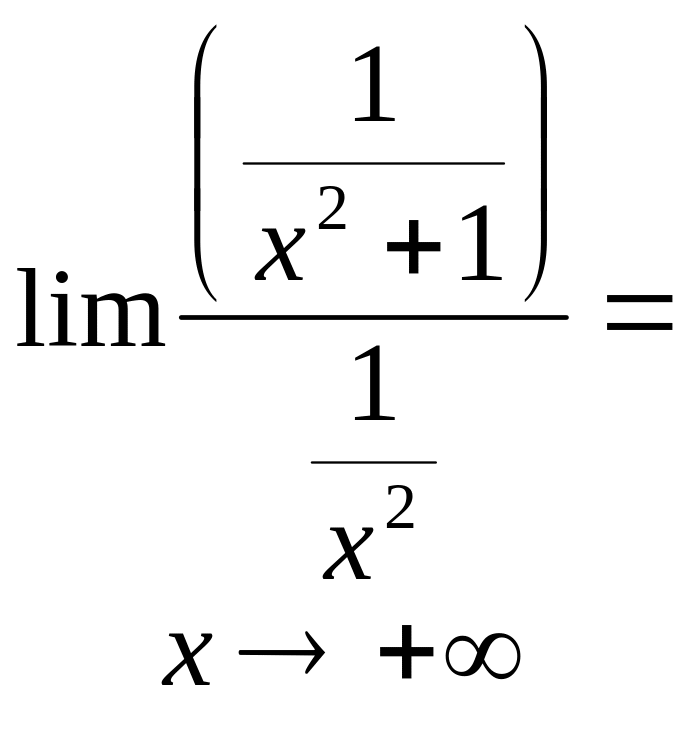
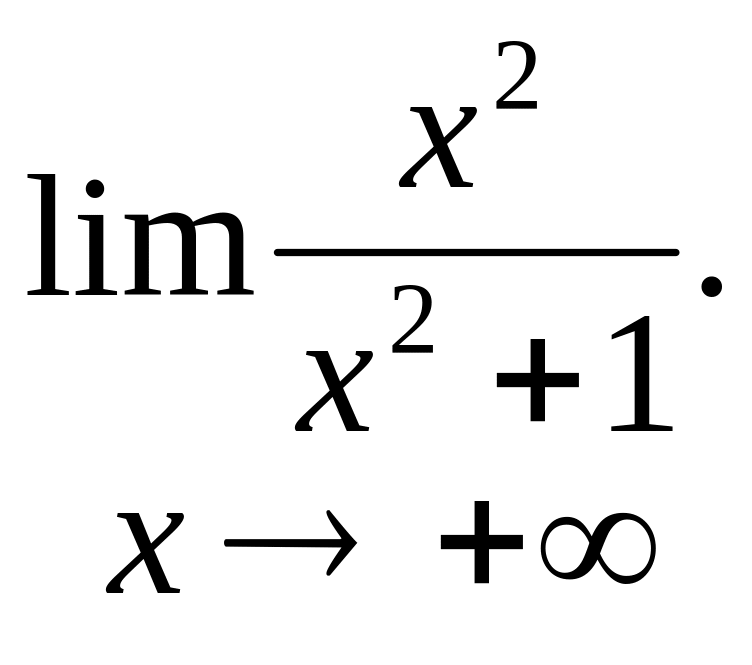 Ми скористалися тим, що ln(1+1/(x2+1))1/(x2+1),
x,
таким
чином за теоремою 2
розбігається, оскільки збіжним є
інтеграл
.
Ми скористалися тим, що ln(1+1/(x2+1))1/(x2+1),
x,
таким
чином за теоремою 2
розбігається, оскільки збіжним є
інтеграл
.
У теормах 1 і 2 розглядаються лише невласні інтеграли від невід’ємних ф-й. У випадку коли підінтегральна ф-я знакозмінна справедлива така теорема:
Теорема
3: Якщо
![]() збігається,
то збігається і
збігається,
то збігається і![]() .
.
Приклад:
Дослідити на збіжність інтеграл.
![]() підінтегральна ф-я знакозмінна.
Розглянемо
підінтегральна ф-я знакозмінна.
Розглянемо
![]() .
.
10
продолжОскільки
|(1+3sin
x)/x4|4/x4;
![]() -
збіжний, тому за теоремою 1 (4
збіжний, а за теоремою 3
-
збіжний.
-
збіжний, тому за теоремою 1 (4
збіжний, а за теоремою 3
-
збіжний.
![]()
![]() .
.
З
збіжності
у
загальному випадку не випливає збіжність
![]() .
.![]()
Означення: Якщо разом з інтегралом збігається інтеграл , то інтеграл називається абсолютно збіжним. У випадку коли збігається, а інтеграл розбіжний, то називається умовно (неабсолютно) збіжним.
