
- •1.Функція багатьох змінних. Границя функції багатьох змінних.
- •2. Неперервність ф-ї багатьох змінних.
- •3.Частинні похідні. Диференцируємость ф-ї багатьох змінних.
- •4.Повний диференціал ф-ї багатьох змінних. Диференціали вищих порядків.
- •5. Похідні складної ф-ї багатьох змінних. Диференціал складної ф-ї багатьох змінних.
- •6. Екстремум ф-ї 2 змінних. Необхідні і достатні умови.
- •7. Невласні інтеграли 1 роду. Приклади.
- •8. Невласні інтеграли 2-го роду.
- •9.Числові ряди Найпростіші властивості.
- •10.Ознаки порівняння додатніх числових рядів.Приклади.
- •11. Знакоочередні ряди. Ознака Лейбніца. Знакозмінні ряди. Абсолютна і умовна збіжності.
- •Теорема2(Абелья) Якщо ряд (1) розбіжний в точці то він буде розбіжним для всіх
- •14.Ряд Тейлора
- •14.2Разложение элементарн. Функций в ряд Макларена
- •15 Тригонометрический ряд Фурье.
4.Повний диференціал ф-ї багатьох змінних. Диференціали вищих порядків.
Нагадаємо, що Ф-я z=f(x,y) диференцируєма в точці М, якщо її повний приріст в цій точці можна надати у вигляді z=Ах+Ву+x+y (1), де А,В – дійсні числа, які не залежать від х,у. х,у), х,у) – нескінченно малі ф-ї, якщо х, у0.
Означення: Повним диференціалом dz, диференцируємої в точці М(х,у) ф-ї z=f(x,y) називається лінійним відносно х,у, частина повного прирісту цієї ф-ї в т. М. Тобто dz=Ах+Ву.
Диференціали
незалежних змінних х та у називаємо
прирісти цих змінних, тобто dх=х,
dу=у,
тоді враховуючи теорему про існування
частинних похідних диференцируємої
ф-ї, формулу (2) можна записати
![]() (3).
(3).
Аналогічна
формула має місце для диференцируємої
ф-ї 3 змінних u=u(x,y,z)
![]() (4).
(4).
Теорема: Різниця між повним прирістом z і повним диференціалом dz є при х, у0 – нескінченно малих вищого порядку ніж g=(х2+у2)1/2.
Доведення:
Зформул (1) і (2) маємо
 ,
оскільки ф-ї
і
- нескінченно малі ф-ї при х,
у0,
а ф-ї х/g,
у/g
–
обмежені (х/(х2+у2)1/2)=1/(1+(dу2/х2)1,
так как dу2/х21
х/g1,
у/g)1
аналогічно.
,
оскільки ф-ї
і
- нескінченно малі ф-ї при х,
у0,
а ф-ї х/g,
у/g
–
обмежені (х/(х2+у2)1/2)=1/(1+(dу2/х2)1,
так как dу2/х21
х/g1,
у/g)1
аналогічно.
Зауваження: Оскільки різниця z-dz – нескінченно мала величина вищого порядку ніж g, то виконується наближена рівність zdz, або f(х+х,у+у)f(x,y)+fx’(х,у)х+ fу’(х,у)у (5).
Ця рівність тим точніша чим менше величина g. Рівність (5) широко використовується в наближених обчисленнях, оскільки диференціал ф-ї обчислюється простіше ніж повний приріст.
Приклад: Знайти повний диференціал ф-ї z=х3у2. Частинні похідні z/х=3х2у2 і z/у=2х3у – неперервні ф-ї у R2 тому диференціал ф-ї на всьому R2 дорівнює dz=3х2у2dx+2х3уdy.
Нехай z=f(x,y) – ф-я 2 незалежних змінних х та у, диференціал ф-ї знайдений за ф-ю (3) називається ще диференціалом 1 порядку.
Означення: Диференціал 2 порядку ф-ї z=f(x,y) визначається як d2z=d(dz).
Нехай
ф-я z=f(x,y)
має неперервні частинні похідні,
знайдемо формулу для диференціала 2
порядку цієї ф-ї. d2z=d(dz)=iз
(3)=![]()
![]()
![]()
![]()
![]()
![]()
![]() Таким чином одержимо (6). Тут ми
використовуємо теорему Шварца. Символічно
(6) можна записати так: d2z=
Таким чином одержимо (6). Тут ми
використовуємо теорему Шварца. Символічно
(6) можна записати так: d2z=![]() .
Аналогічно можна довести d3z=
.
Аналогічно можна довести d3z=![]() .
Застосовуючи метод математичної
індукції одержимо формулу для диференціала
n
порядку dnz=
.
Застосовуючи метод математичної
індукції одержимо формулу для диференціала
n
порядку dnz=![]() ,
де dnz=d(dn-1z)
(7).
,
де dnz=d(dn-1z)
(7).
Зауваження: Формули (6) і (7) справедливі лише у випадку коли змінні х,у в ф-ї z=f(x,y) є незалежними.
5. Похідні складної ф-ї багатьох змінних. Диференціал складної ф-ї багатьох змінних.
Нехай z=f(x,y) ф-я 2 змінних х, у, кожна з яких, в свою чергу ф-я незалежної змінної t (x=x(t), y=y(t)), тоді z=f(x(t),y(t)) є складена ф-я змінної t.
Теорема:
Нехай ф-ї x=x(t),
y=y(t)
диференцируємі у т. t,
а ф-я z=f(x,y)
диференцируєма у відповідній точці
М(х,у), тоді складена ф-я z=f(x(t),y(t))
диференцируєма в т. t
і її похідну можна знайти за формулою:
![]() (1).
(1).
Доведення:
За умовою теореми



![]()
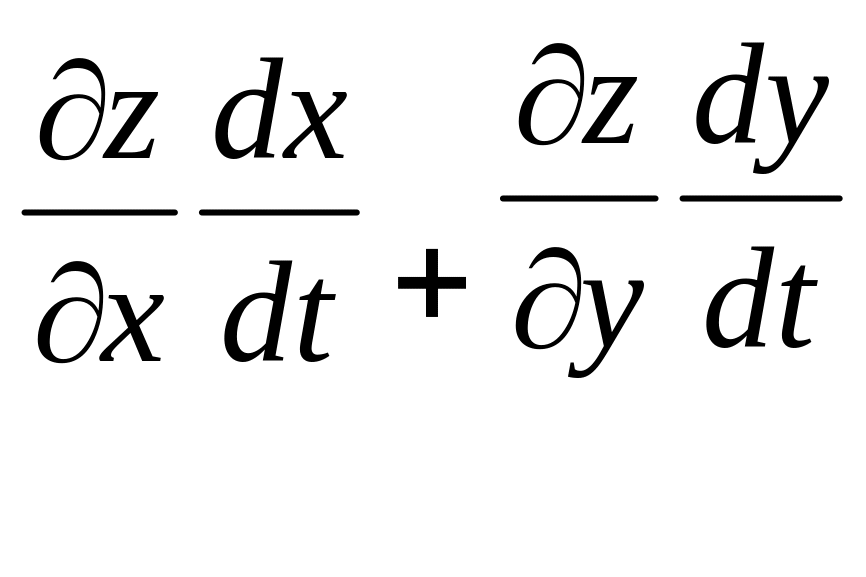 ,
т. к.,
,
т. к.,
![]() Оскільки з умови диференцируємості
ф-ї випливає їх неперервність, то з
того, що
Оскільки з умови диференцируємості
ф-ї випливає їх неперервність, то з
того, що
![]() маємо
маємо
![]()
![]()
Приклад: Знайти похідну dz/dt, якщо z=x2-3y, де x=2t, y=t2. Знайдемо похідні z/x=2x-3y; z/y=-3x; dx/dt=2; dy/dt=2t. За формулою (1) одержимо Dz/dt=(2x-3y)2+(-3x)2t=22t2-3t22+(-32t2t)=8t-6t2-12t2=8t-18t2 .
Аналогічно знаходять похідну, якщо число змінних більше 2.
Наприклад:
u=f(x,y,z),
x=x(t),
y=y(t),
z=z(t)
du/dt= .
.
Розглянемо більш загальний випадок, нехай z=f(x,y) у якої кожна з змінних , у свою чергу є ф-я 2 змінних u,v. x=x(u,v), y=y(u,v), тоді z=f(x(u,v),y(u,v)) визначає складену ф-ю змінних u і v.
Теорема:
Якщо ф-ї x=x(u,v),
y=y(u,v)
диференцируємі у т. М1(u,v),
а ф-я z=f(x,y)
диференцируєма в т. М(х,у), то складена
ф-я z=f(x(u,v),y(u,v))
диференцируєма у т. М(u,v)
і її частинні похідні можна знайти за
формулами:
![]()
![]() .
Доводиться аналогічно попередній.
.
Доводиться аналогічно попередній.
Знайти z/u, z=x2ln y, де x=u/v;y=uv. Знаходимо частинні похідні: z/х=2xln у; z/у=х2/у; х/u=1/v; y/u=v за (2): z/u=2х ln y 1/v+ х2 v /у=2 u/vln uv1/v+ u2/ v2*
*(2ln uv+1).
Знайдемо диференціал складної ф-ї:
dz=(z/u) d u+(z/ v) d v=(z/х*х/ v+z/у*y/u)d u+(z/х*х/ v+z/у*у/v)dv=
=z/х((х/u)du+(х/ v) d v)+ z/у((y/u) d u+(у/v) d v)= (z/х) dx+ (z/у) dy(3).
Порівнюючи (3) з формулою (3) пит 5 одержимо що dz ф-ї z=f(x,y) має незмінну і інваріантну форму незалежно від того чи є змінні х,у незалежними зм-ми , чи х,у –ф-ї від змінних u,v.
Заув-ня: Диф-ли вищих порядків не мають властивості інваріантності.
Приклад:
z=f(x,y), х=х(u,v), у=у(u,v)
2z= dz(dz)= d((z/х)dx +(z/у)dy)= (2z/х2)dx2 +2(2z/(ху))dxdy+(2z/у2) dy2+
(z/х) 2х=(z/у) 2у (4).
Порівнюючи ф-лу (4) з ф-ю (6) теми 5, бачимо, що у (4) є 2 доданки, яких не має в (6), тому ці ф-ли не співпадають і диференціали не мають вищих порядків.
