1. Первообразная и неопределенный интеграл. Теорема об общем виде

первообразной.

Функция F(x) называется первообразной функции f(x) на интервале (a; b), если для любого x∈(a; b) выполняется равенство F’(x)=f(x) или dF(x)=f(x) dx.

Неопределенный интеграл – множество всех первообразных функций F(x)+C для f(x) и обозначается символом ∫f(x) dx. По определению ∫f(x) dx=F(x)+C, где f(x)-подынтегральная функция, f(x) dx-подынтегральное выражение, x-переменная интегрирования.

Теорема: Если функция F(x) является первообразной функции f(x) на (a;b), то множество всех первообразных для f(x) задается формулой F(x)+C, где C-постоянное число.

Док-во: Функция F(x)+C является первообразной f(x). Действительно, (F(x)+C)’=F’(x)=f(x). Пусть Ф(х) – отличная от F(x), первообразная функции f(x), т.е. Ф’(x)=f(x). Тогда для любого x∈(a; b) имеем (Ф(х)-F(x))’=Ф’(x)-F’(x)=f(x)-f(x)=0. А это означает, что Ф(х)-F(x)=C. Следовательно Ф(х)=F(x)+C.

2. Основные свойства неопределенных интегралов.

1 св-во-Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции: d (∫f(x) dx)=f(x) dx, (∫f(x) dx)’=f(x)

2 св-во-Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной: ∫dF(x)=F(x)+C

3 св-во-Постоянный множитель можно выносить за знак интеграла

4 св-во-Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций

5 св-во-Инвариантность формулы интегрирования: Если ∫f(x) dx=F(x)+C, то и ∫ f(u) du=F(u)+C, где u-произвольная функция, имеющая непрерывную производную

3. Метод интегрирования разложением и подстановкой. Теорема о замене

переменной в неопределенном интеграле.

Теорема: Пусть функция f(x) определена на множестве Х, а функция φ(t) – на множестве Φ, причем φ(t) ∈ Х. Тогда, если функция f(x) имеет первообразную F(x) на Х, а φ(t) дифференцируема на Φ, то ∫f(x) dx=∫f(φ(t))*φ’(t) dt

Док-во:

поэтому функция F(φ(t)) является первообразной функции f(φ(t)) φ’(t). Следовательно,

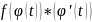∫ dt =F +C. С другой стороны, при x = φ(t) ∫f(x) dx=F )+C. В полученных формулах равны правые части, следовательно, равны и левые.

4. Метод интегрирования по частям. Теорема.

Теорема: ∫u dv=uv-∫v du

Док-во: Пусть u=u(x), v=v(x) – функции, имеющие непрерывные производные. Тогда d(uv)=u*dv+v*du. Интегрируя это равенство мы получим ∫d(uv)= ∫u dv+∫v du или исходную формулу.

5. Интегрирование простейших дробей.

Это дроби типа , ,

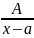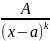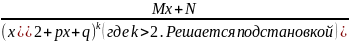
6. Интегрирование дробно-рациональных функций.

Это функция, равная отношению двух многочленов, т.е. f(x)=P(x)/Q(x). Если дробь неправильная (степень многочлена в числителе больше), то выполняется деление числителя на знаменатель (представить дробь в виде суммы многочлена и правильной дроби). Далее разложить знаменатель правильной дроби на множители представить ее в виде суммы простейших дробей. И проинтегрировать многочлен и полученную сумму простейших дробей.