
- •1. Первообразная и неопределенный интеграл. Теорема об общем виде
- •2. Основные свойства неопределенных интегралов.
- •3. Метод интегрирования разложением и подстановкой. Теорема о замене
- •4. Метод интегрирования по частям. Теорема.
- •5. Интегрирование простейших дробей.
- •6. Интегрирование дробно-рациональных функций.
- •7. Интегрирование иррациональных выражений.
- •8. Интегрирование тригонометрических функций.
- •17.Несобственные интегралы с бесконечными пределами. Теорема о сходимости таких интегралов.
- •18. Несобственные интегралы от неограниченных функций.
- •19. Абсолютная сходимость несобственных интегралов.
- •20. Числовые ряды. Частичные суммы. Сходимость ряда. Теорема об общем члене сходящегося ряда.
- •21. Основные свойства рядов. Остаток ряда. Теорема об остатке ряда.
- •22. Положительные ряды. Признаки сходимости (теоремы сравнения)
- •23. Признак Даламбера.
- •24. Радикальный признак Коши.
- •25. Интегральный признак Коши-Маклорена.
- •26. Знакопеременные ряды. Понятие абсолютной сходимости. Теорема Коши об абсолютной сходимости.
- •27. Условная сходимость рядов. Теорема Лейбница.
- •28. Функциональные ряды. Область сходимости.
- •29. Степенные ряды. Теорема Абеля.
- •30. Ряды Тейлора. Критерий разложимости функции в ряд Тейлора.
- •35. Линейные уравнения первого порядка. Метод вариации произвольной постоянной (Лагранжа).
- •36. Уравнение Бернулли.
- •37. Задача Коши для уравнения первого порядка, разрешенного относительно производной.
- •38. Дифференциальные уравнения порядка выше первого. Два типа уравнений, метод решений которых понижение порядка.
- •39. Линейная зависимость функций. Определитель Вронского.
- •40. Однородные линейные дифференциальные уравнения с постоянными коэффициентами.
- •41. Неоднородные линейные дифференциальные уравнения с постоянными коэффициентами.
- •46. Частные производные высших порядков. Дифференцируемость функций нескольких переменных.
- •47. Дифференцирование сложных функций многих переменных.
- •48. Инвариантность формулы первого дифференциала.
- •49. Касательная плоскость и нормаль к поверхности.
- •50. Полные дифференциалы высших порядков.
- •51. Формула Тейлора для функции нескольких переменных.
- •52. Экстремум функции двух переменных. Необходимое условие экстремума. Достаточное условие экстремума.
28. Функциональные ряды. Область сходимости.
Ряд,
членами которого являются функции от
х, называется функциональным:
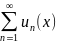 =
=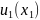 +
+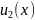 +…+
+…+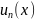 +…,
+…,
Придавая
х определенное значение
 ,
получим ряд
,
получим ряд
 +
+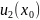 +…+
+…+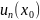 +…,
+…,
Если полученный числовой ряд сходится, то точка называется точкой сходимости данного ряда. Если же ряд расходится, то точкой расходимости.
29. Степенные ряды. Теорема Абеля.
Степенной ряд – это ряд, членами которого являются степенные функции аргумента х.
 =
= +
+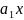 +
+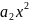 + … +
+ … +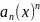 +…(1), где
+…(1), где
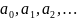 - коэффициенты ряда
- коэффициенты ряда
Теорема
Абеля: Если
степенной ряд (1) сходится при
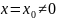 ,
то он абсолютно сходится при всех
значениях х, удовлетворяющих неравенству
,
то он абсолютно сходится при всех
значениях х, удовлетворяющих неравенству
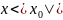 .
.
Док-во:
По
условию ряд
 сходится. Следовательно, по необх. приз.
сходимости
сходится. Следовательно, по необх. приз.
сходимости
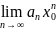 = 0. Отсюда следует, что величина
= 0. Отсюда следует, что величина
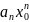 ограничена,
т.е. найдется такое число M>0,
что для всех n
выполняется неравенство
ограничена,
т.е. найдется такое число M>0,
что для всех n
выполняется неравенство
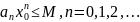 Пусть
|x|<|
|,
тогда величина q=
Пусть
|x|<|
|,
тогда величина q=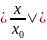 <1
и, следовательно,
<1
и, следовательно,
|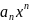 |=
|=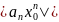 |
|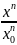 |
|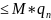 ,
,
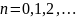 То есть модуль каждого члена исходного
ряда не превосходит соответствующего
члена сходящегося ряда. Поэтому по пр.
ср. ряд сходится абсолютно.
То есть модуль каждого члена исходного
ряда не превосходит соответствующего
члена сходящегося ряда. Поэтому по пр.
ср. ряд сходится абсолютно.
30. Ряды Тейлора. Критерий разложимости функции в ряд Тейлора.
Если функция f(x) имеет производные любых порядков в окрестности точки и остаточный член стремится к нулю , то из формулы Тейлора получается разложение функции f(x) по степеням (x- ), называемое рядом Тейлора:
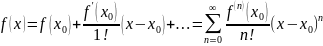
Теорема: Если модули всех произвольных функций f(x) ограничены в окрестности точки одним и тем же числом M>0, то для любого x из этой окрестности ряд Тейлора функции f(x) сходится к функции f(x), т.е. имеет место разложение в ряд Тейлора.
Доказательство длинное. Покажите, что остаточный член стремится к нулю и все получится.
31. Разложение функций в степенные ряды.
Написать разложения основных функций.
32. Приложения рядов для приближенных вычислений.
Раскладывать по известным разложениям функций. Используя точность (кол-во знаков после запятой), чтобы отбросить нужный остаточный член.
33. Дифференциальные уравнения первого порядка. Уравнения с разделяющимися переменными.
Дифференциальное уравнение – это уравнение, в котором связана независимая переменная, искомая функция и ее производные. ДУ 1 порядка – это уравнение вида y’=f(x; y). Оно имеет вид P(x)dx+Q(y)dy=0. Как видно, переменные резделены. Чтобы его решить, нужно почленно проинтегрировать это уравнение. Тогда получим
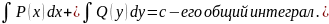
34. Уравнения с однородными коэффициентами. Метод подстановки.
Функция
f(x;
y)
называется однородной функцией n-го
порядка, если при умножении каждого ее
аргумента на произвольный множитель λ
вся функция умножится на
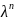 ,
т.е. f(λx;
λy)=
,
т.е. f(λx;
λy)=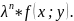
ДУ y’=f(x; y) называется однородным, если f(x; y) есть однородная функция 0 порядка.
Однородное
ДУ можно записать в виде y’=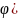 )
(1).
)
(1).
Если
f(x;
y)
– однородная функция 0 порядка, то по
определению, f(x;
y)=f(λx;
λy).
Заменив λ=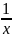 ,
получаем f(x;
y)=
f(
,
получаем f(x;
y)=
f(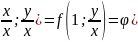 ).
).
Однородное
уравнение (1) преобразуется в уравнение
с разделяющимися переменными при помощи
подстановки
 или y=ux.
Действительно, подставив данные в
исходное уравнение получаем уравнение
с разделяющимися переменными.
или y=ux.
Действительно, подставив данные в
исходное уравнение получаем уравнение
с разделяющимися переменными.
