7. Интегрирование иррациональных выражений.

Встречаются квадратичные иррациональности. Решаются выделением полного квадрата под радикалом и последующей подстановкой

8. Интегрирование тригонометрических функций.

Используется универсальная подстановка tg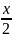 =t. Тогда sin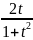(x)= , cos(x)=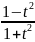 , x=2arctg(t), dx=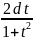

Если функция нечетна относительно sin(x), выполняется подстановка cos(x)=t

Если функция нечетна относительно cos(x), выполняется подстановка sin(x)=t

Если функция четна относительно sin(x) и cos(x), применяется tg(x)=t

Интегралы типа ∫ * 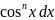решаются подстановкой

• sin(x)=t, если n-нечетное,

• cos(x)=t, если m-нечетное,

• формулы понижения степени 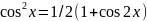, ,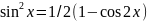sin(x)*cos(x)=1/2*sin2x, если m и n-четные

• tg(x)=t, если m+n=четное

9. Определенный интеграл и его тригонометрический смысл.

Определенный интеграл - это интеграл вида , где a и b – нижний и верхний пределы интегрирования, f(x) – подынтегральная функция, отрезок [a; b] – область интегрирования.

Если функция f(x) непрерывна на отрезке [a; b], то определенный интеграл существует (по теореме Коши)

Геометрический смысл – определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.

10. Верхние и нижние суммы Дарбу. Критерий интегрируемости.

Пусть на отрезке [a; b] задана ограниченная функция f (|f(x)|≤M). Введем разбиение

R: a=x₀<x₁<…<x_n=b. Пусть m=inf f(x), M=sup f(x). Суммы s_R=∑ m∆x, S_R=∑ M∆x называют нижней и верхней суммами Дарбу. Очевидно, что s_R≤S_R

11. Свойства определенных интегралов, связанные с равенствами.

1)Постоянный множитель С можно выносить за знак определенного интеграла

2)Определенный интеграл от суммы равен сумме определенных интегралов

3)

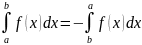
4)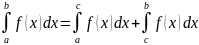 , если a<c<b. Аддитивность опр. инт.

12. Свойства определенных интегралов, связанные с неравенствами.

1)Если функция f(x) сохраняет знак на отрезке [a; b], где a<b, то интеграл имеет тот же знак, что и функция

2)Неравенство между непрерывными функциями на отрезке [a; b], (a<b) можно интегрировать

3)Если m и M – наименьшее и наибольшее значения функции y=f(x) на отрезке [a; b], (a<b), то m(b-a) ≤ ≤ M(b-a)

4)Модуль определенного интеграла не превосходит интеграла от модуля подынтегральной функции

13. Теорема о среднем для определенного интеграла.

Теорема: Если функция f(x) непрерывна на отрезке [a; b], то существует точка с∈ [a; b] такая, что

Док-во: По формуле Ньютона-Лейбница имеем 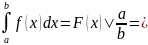F(b) – F(a), где F’(x)=f(x). Применяя к данной разности теорему о конечном приращении функции (Лагранжа), получим F(b) – F(a)=F’(c)*(b-a)=f(c)*(b-a)

14. Определенный интеграл с переменным верхним пределом

Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, в которой переменная интегрирования заменена этим пределом.

_x’ = f(x)

Док-во: По формуле Ньютона-Лейбница имеем 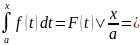F(x) – F(a). Следовательно, _x’=(F(x)-F(a))_x’ = F’(x)-0 = f(x).

15. Центральная теорема интегрального исчисления о связи первообразной

и определенного интеграла с переменным верхним пределом. Формула

Ньютона-Лейбница.

Определенны интеграл с переменным верхним пределом есть одна из первообразных подынтегральной функции. Следовательно для вычисления определенного интеграла нужно вычислить неопределенный интеграл, а потом применить формулу Ньютона-Лейбница: 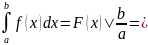F(b) – F(a).

16. Вычисление длины дуги кривой. Площадь поверхности вращения.

Длина дуги - предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а а длина наибольшего звена ее стремится к нулю.

Если функция и ее производная непрерывны на отрезке [a; b], то кривая имеет длину l=

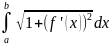
Площадь плоской фигуры равна соответствующему определенному интегралу. Т.е. S= .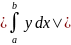

Площадь кривой, ограничивающей криволинейную трапецию, заданная параметрически x=x(t), y=y(t), t∈[α; β], прямыми x=a и x=b и осью Ох, равна S=| |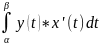

Если плоская фигура ограничена непрерывной линией r=r(φ) и двумя лучами φ= α и φ= β (α< β), где r и φ – полярные координаты, то S=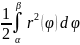

Пусть кривая AB является графиком функции y=f(x)≥0, где x∈[α; β], а функция y=f(x) и ее производная y’=f’(x) на этом отрезке. Площадь поверхности вращения

S_x=2 dx.

Если кривая задана параметрическими уравнениями x=x(t), y=y(t), t₁≤t≤t₂, то S_x=2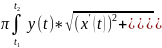 dt