
- •1. Первообразная и неопределенный интеграл. Теорема об общем виде
- •2. Основные свойства неопределенных интегралов.
- •3. Метод интегрирования разложением и подстановкой. Теорема о замене
- •4. Метод интегрирования по частям. Теорема.
- •5. Интегрирование простейших дробей.
- •6. Интегрирование дробно-рациональных функций.
- •7. Интегрирование иррациональных выражений.
- •8. Интегрирование тригонометрических функций.
- •17.Несобственные интегралы с бесконечными пределами. Теорема о сходимости таких интегралов.
- •18. Несобственные интегралы от неограниченных функций.
- •19. Абсолютная сходимость несобственных интегралов.
- •20. Числовые ряды. Частичные суммы. Сходимость ряда. Теорема об общем члене сходящегося ряда.
- •21. Основные свойства рядов. Остаток ряда. Теорема об остатке ряда.
- •22. Положительные ряды. Признаки сходимости (теоремы сравнения)
- •23. Признак Даламбера.
- •24. Радикальный признак Коши.
- •25. Интегральный признак Коши-Маклорена.
- •26. Знакопеременные ряды. Понятие абсолютной сходимости. Теорема Коши об абсолютной сходимости.
- •27. Условная сходимость рядов. Теорема Лейбница.
- •28. Функциональные ряды. Область сходимости.
- •29. Степенные ряды. Теорема Абеля.
- •30. Ряды Тейлора. Критерий разложимости функции в ряд Тейлора.
- •35. Линейные уравнения первого порядка. Метод вариации произвольной постоянной (Лагранжа).
- •36. Уравнение Бернулли.
- •37. Задача Коши для уравнения первого порядка, разрешенного относительно производной.
- •38. Дифференциальные уравнения порядка выше первого. Два типа уравнений, метод решений которых понижение порядка.
- •39. Линейная зависимость функций. Определитель Вронского.
- •40. Однородные линейные дифференциальные уравнения с постоянными коэффициентами.
- •41. Неоднородные линейные дифференциальные уравнения с постоянными коэффициентами.
- •46. Частные производные высших порядков. Дифференцируемость функций нескольких переменных.
- •47. Дифференцирование сложных функций многих переменных.
- •48. Инвариантность формулы первого дифференциала.
- •49. Касательная плоскость и нормаль к поверхности.
- •50. Полные дифференциалы высших порядков.
- •51. Формула Тейлора для функции нескольких переменных.
- •52. Экстремум функции двух переменных. Необходимое условие экстремума. Достаточное условие экстремума.
17.Несобственные интегралы с бесконечными пределами. Теорема о сходимости таких интегралов.
Несобственный интеграл – это определенный интеграл от непрерывной функции, но с бесконечным промежутком интегрирования или определенный интеграл с конечным промежутком интегрирования, но от функции, имеющей на нем бесконечный разрыв.
Пусть
функция f(x)
непрерывна на промежутке [a;
+∞). Если существует конечный предел
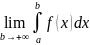 ,
то его называют несобственным интегралом
1 рода и обозначают
,
то его называют несобственным интегралом
1 рода и обозначают
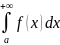 .
Т.е
.
Т.е
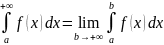 .
В этом случае несобственный интеграл
сходится. А если указанный предел не
существует или бесконечен, то интеграл
расходится.
.
В этом случае несобственный интеграл
сходится. А если указанный предел не
существует или бесконечен, то интеграл
расходится.
Теорема (пр. ср.): Из сходимости большего интеграла следует сходимость меньшего
Теорема:
Если существует предел
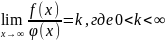 ,
то интегралы ведут себя одинаково в
плане сходимости.
,
то интегралы ведут себя одинаково в
плане сходимости.
18. Несобственные интегралы от неограниченных функций.
Пусть
функция f(x)
непрерывна на промежутке [a;
b)
и имеет бесконечный разрыв при x=b.
Если существует конечный предел
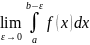 ,
то его называют несобственным интегралом
2 рода и обозначают
.
,
то его называют несобственным интегралом
2 рода и обозначают
.
Т.е. = . Если предел в правой части существует, то несобственный интеграл сходится.
Теорема (пр. ср.): Из сходимости большего интеграла следует сходимость меньшего
Теорема:
Если существует предел
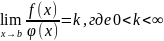 ,
то интегралы ведут себя одинаково в
плане сходимости (b-точка
разрыва).
,
то интегралы ведут себя одинаково в
плане сходимости (b-точка
разрыва).
19. Абсолютная сходимость несобственных интегралов.
Для
беск. Пределов: Если сходится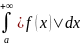 ,
то сходится
абсолютно
,
то сходится
абсолютно
Для
неогр. Функций: Если сходится
 ,
то сходится
абсолютно
,
то сходится
абсолютно
20. Числовые ряды. Частичные суммы. Сходимость ряда. Теорема об общем члене сходящегося ряда.
Числовой
ряд – выражение вида
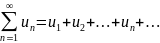 ,
где
,
где
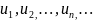 -
члены ряда,
-
члены ряда,
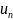 – общий член
– общий член
Сумма первых n членов рада называется n-й частичной суммой ряда и обозначается Sn.
Если
существует конечный предел S=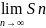 ,
то этот предел – сумма ряда, и ряд
сходится. Если предел не существует или
равен бесконечности, то ряд расходится.
,
то этот предел – сумма ряда, и ряд
сходится. Если предел не существует или
равен бесконечности, то ряд расходится.
21. Основные свойства рядов. Остаток ряда. Теорема об остатке ряда.
Свойство 1: Если ряд сходится, его сумма равна S и в нем каждый член ряда умножить на произвольную константу, то получившийся ряд также сходится и сумма его равна cS
Свойство
2: Если сходится ряд
и сходится ряд
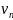 ,
а их суммы равны S1
и S2
соответственно, то сходятся и ряды
,
а их суммы равны S1
и S2
соответственно, то сходятся и ряды
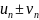 и сумма каждого равна S1
± S2
и сумма каждого равна S1
± S2
Свойство 3: Если к ряду прибавить или отбросить конечное число членов, то полученный ряд и первоначальный ряд сходятся или расходятся одновременно.
Ряд
un+1
+
un+2
+…
=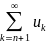 называется n-м
остатком ряда
называется n-м
остатком ряда
 .
Следовательно, исходя из свойства 3
исходный ряд и получившийся ряд
одновременно сходятся или расходятся.
Если ряд
сходится, то его остаток стремится к
нулю при n
.
Следовательно, исходя из свойства 3
исходный ряд и получившийся ряд
одновременно сходятся или расходятся.
Если ряд
сходится, то его остаток стремится к
нулю при n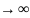
22. Положительные ряды. Признаки сходимости (теоремы сравнения)
Теорема
пр.ср.:
Пусть даны два знакоположительных ряда
(1),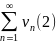 .
Если для всех n
выполняется равенство un≤vn,
то из сходимости (2) ряда следует сходимость
(1). Из расходимости (1) ряда следует
расходимость (2).
.
Если для всех n
выполняется равенство un≤vn,
то из сходимости (2) ряда следует сходимость
(1). Из расходимости (1) ряда следует
расходимость (2).
Док-во:
Из
неравенства un≤vn
следует,
что n-я
частичная сумма (2) ряда больше или равна
частичной сумме (1) ряда (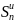 ≤
≤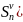 .
Пусть ряд (2) сходится и его сумма равна
S2.
Тогда
.
Пусть ряд (2) сходится и его сумма равна
S2.
Тогда
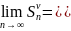 S2.
Члены
ряда (2) положительны, поэтому
S2.
Члены
ряда (2) положительны, поэтому
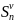 <S2
и с учетом неравенства
≤
,
≤S2.
Таким образом, последовательность
<S2
и с учетом неравенства
≤
,
≤S2.
Таким образом, последовательность
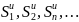 монотонно возрастает (un>0)
и ограничена сверху числом S2.
По признаку существования предела
последовательность
имеет предел
монотонно возрастает (un>0)
и ограничена сверху числом S2.
По признаку существования предела
последовательность
имеет предел
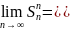 S1,
т.е. ряд сходится.
S1,
т.е. ряд сходится.
Пусть
теперь ряд (1) расходится. Так как члены
ряда неотрицательны, в этом случае имеем
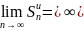 .
С учетом неравенства
≤
следует, что
.
С учетом неравенства
≤
следует, что
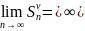 .
Т.е. ряд (2) расходится.
.
Т.е. ряд (2) расходится.
Теорема
(предельный пр. ср): Пусть
даны два знакоположительных ряда (1) и
(2). Если существует конечный, отличный
от 0 предел
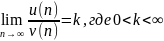 ,
то ряды (1) и (2) сходятся или расходятся
одновременно.
,
то ряды (1) и (2) сходятся или расходятся
одновременно.
Док-во:
Пусть
(A-ɛ)vn<un<(A+ɛ)vn
Если
ряд (1) сходится, то из левого неравенства
и теоремы пр. ср. вытекает, что
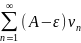 также сходится. Следовательно, тогда и
ряд (2) сходится. Если ряд (1) расходится,
то их правого равенства и теоремы пр.
ср. вытекает, что рад (2) расходится.
также сходится. Следовательно, тогда и
ряд (2) сходится. Если ряд (1) расходится,
то их правого равенства и теоремы пр.
ср. вытекает, что рад (2) расходится.
