
- •Бийский технологический институт (филиал)
- •Теория вероятностей и математическая статистика
- •Введение
- •События. Классификация событий. Классическое определение вероятности
- •Статистическое определение вероятности
- •Геометрическая вероятность
- •Контрольные вопросы
- •Контрольные задания
- •4. Операции над событиями. Соотношения между событиями
- •5.Теорема сложения вероятностей
- •6. Теорема умножения вероятностей
- •Контрольные вопросы
- •Контрольные задания
- •7. Формула полной вероятности
- •8. Теорема гипотез (формула Бейеса)
- •Контрольные вопросы
- •Контрольные задания
- •Литература
- •9. Повторение опытов. Формула Бернулли
- •10. Локальная формула Муавра-Лапласа. Формула Пуассона
- •11. Интегральная формула Муавра-Лапласа. Вероятность отклонения частоты события от его вероятности в n независимых испытаниях
- •Контрольные вопросы
- •Контрольные задания
- •Литература
- •12. Понятие случайной величины. Ряд распределения. Многоугольник распределения
- •13. Функция распределения. Вероятность попадания непрерывной случайной величины в заданный интервал
- •Контрольные вопросы
- •Контрольные задания
- •14. Плотность распределения
- •Контрольные вопросы
- •Контрольные задания
- •15. Числовые характеристики случайных величин. Математическое ожидание и его свойства
- •Свойства математического ожидания
- •16. Дисперсия и ее свойства. Среднее квадратическое отклонение
- •17. Моменты распределения случайной величины
- •Контрольные вопросы
- •Контрольные задания
- •18. Типы распределений дискретных случайных величин
- •Биномиальное распределение
- •18.2 Гипергеометрическое распределение
- •18.3 Геометрическое распределение
- •4. Распределение Пуассона
- •Контрольные вопросы
- •Контрольные задания
- •19. Типы распределений непрерывных случайных величин
- •19.1 Равномерное распределение
- •19.2 Показательное распределение
- •20. Нормальный закон распределения
- •21. Вероятность попадания нормально распределенной случайной величины в заданный интервал. Правило трёх сигма
- •Контрольные вопросы
- •Контрольные задания
- •Литература
- •22. Понятие системы случайных величин
- •23. Закон распределения вероятностей дискретной двумерной случайной величины
- •Контрольные вопросы
- •24. Функция распределения двух случайных величин. Вероятность попадания случайной величины в полуполосу и прямоугольник
- •25. Плотность распределения системы двух случайных величин. Законы распределения отдельных величин, входящих в систему
- •26. Условные законы распределения
- •Контрольные вопросы
- •27. Зависимые и независимые случайные величины
- •28. Числовые характеристики составляющих системы двух случайных величин. Условное математическое ожидание
- •29. Корреляционный момент. Коэффициент корреляции
- •30. Коррелированность и зависимость случайных величин
- •Если величины независимы, то они некоррелированы.
- •31. Линейная регрессия. Прямые линии среднеквадратической регрессии
- •Контрольные вопросы
- •Контрольные задания
- •Литература
- •32. Закон больших чисел
- •33. Центральная предельная теорема
- •Контрольные вопросы
- •Контрольные задания
- •Литература
- •Математическая статистика
- •34. Понятие о выборочном методе. Генеральная и выборочная совокупность
- •35. Статистические данные и их представление
- •36. Статистические аналоги теоретических законов распределения
- •36.1 Эмпирическая функция распределения
- •36.2 Полигон и гистограмма
- •Контрольные вопросы
- •Контрольные задания
- •Литература
- •37. Точечное оценивание параметров распределения
- •38. Свойства статистических оценок
- •Контрольные вопросы
- •Контрольные задания
- •39. Интервальное оценивание параметров распределения
- •40. Интервальное оценивание параметров нормального распределения
- •40.1 Интервальная оценка математического ожидания нормального распределения при известной дисперсии
- •40.2 Интервальная оценка математического ожидания нормального распределения при неизвестной дисперсии
- •Контрольные вопросы
- •Контрольные задания
- •Литература
- •41. Статистические гипотезы
- •42. Критерии проверки гипотез
- •Контрольные вопросы
- •Контрольные задания
- •43.Критерий согласия Пирсона «Хи-квадрат» ( )
- •Контрольные вопросы
- •Контрольные задания
- •Литература
- •44. Элементы теории корреляции. Задачи корреляционного анализа
- •45. Выбор формы зависимости между переменными. Метод наименьших квадратов
- •Контрольные вопросы
- •46. Коэффициент корреляции и проверка его значимости. Линейная регрессия и прогноз
- •Контрольные вопросы
- •Контрольные задания
- •Литература
- •Глоссарий
Контрольные задания
Можно ли подобрать постоянную С так, чтобы функция
 определяла плотность распределения
вероятностей на интервале: а)
определяла плотность распределения
вероятностей на интервале: а)
 ;
б)
;
б)
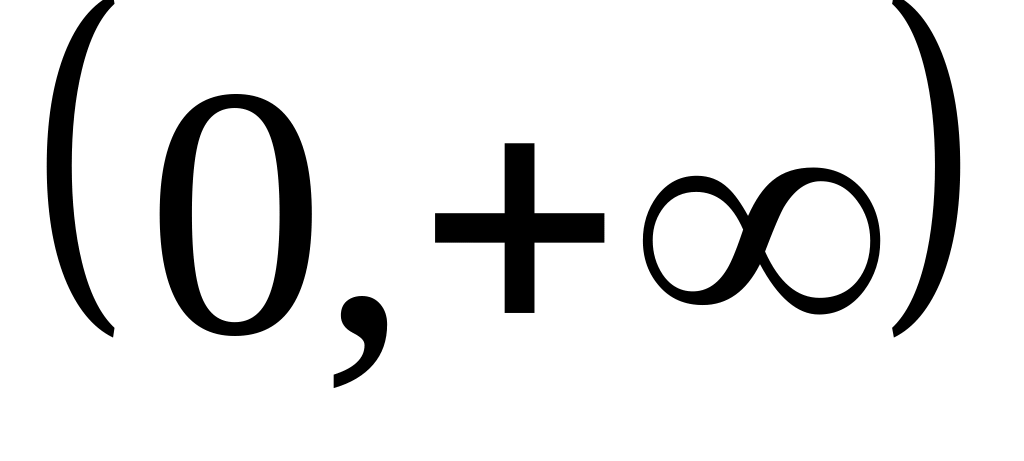 ;
в)
;
в)
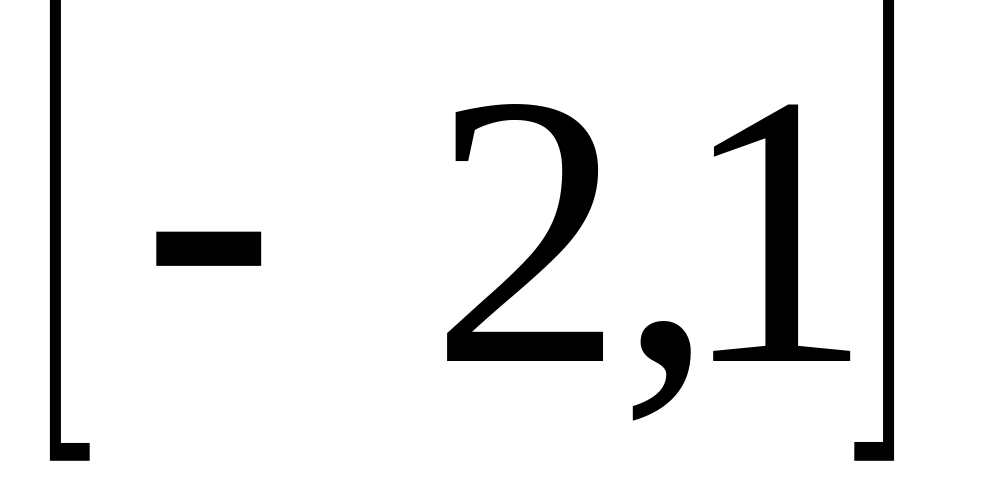 ?
?Непрерывная СВ Х имеет плотность распределения:
а)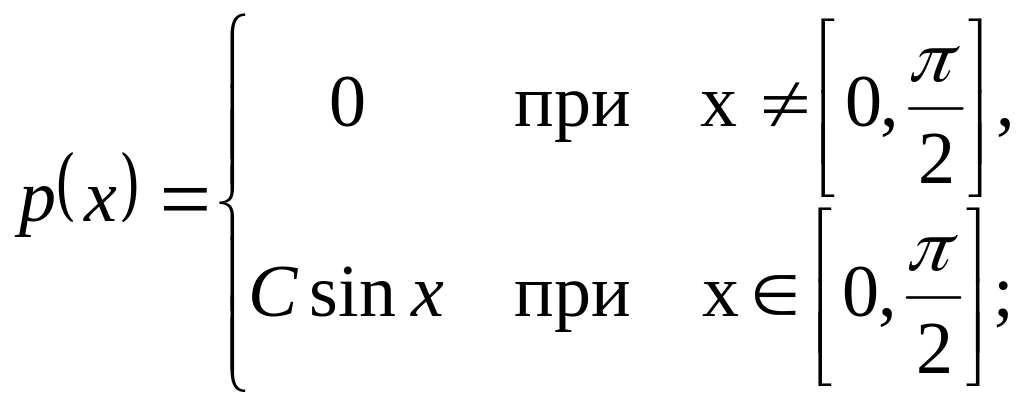 б)
б)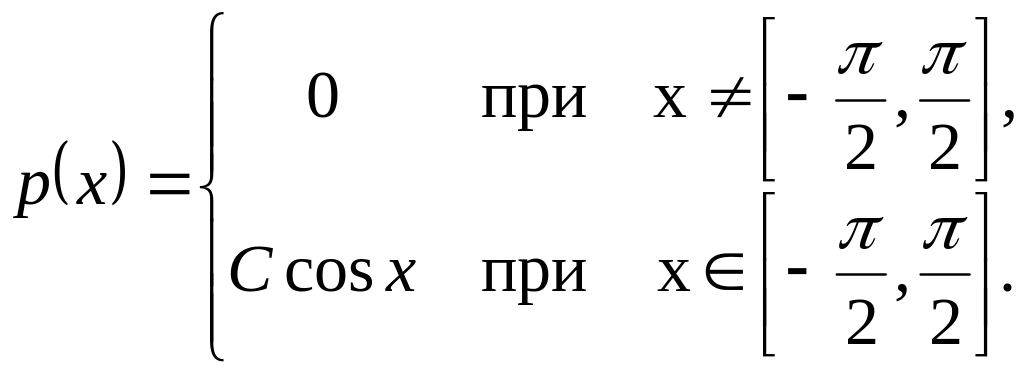
Для каждого распределения необходимо:
1) найти неизвестный параметр С и построить график плотности распределения;
2) найти функцию распределения и построить ее график;
3) вычислить
![]() и
и
![]() ;
;
4) проиллюстрировать вероятности п.3) на графике плотности распределения.
15. Числовые характеристики случайных величин. Математическое ожидание и его свойства
Ранее было отмечено, что полностью характеризуют дискретную случайную величину – функция распределения, ряд распределения; непрерывную случайную величину – функция распределения, плотность распределения.
Однако во многих вопросах практики нет необходимости характеризовать случайную величину полностью, достаточно бывает указать только отдельные числовые параметры, характеризующие существенные черты распределения случайной величины. Например, среднее значение случайной величины, вокруг которого группируются значения этой случайной величины, какое-либо число, характеризующее разбросанность значений случайной величины около среднего значения. Такие характеристики, назначение которых выразить в сжатой форме наиболее существенные особенности распределения, называются числовыми характеристиками случайной величины.
Рассмотрим дискретную случайную величину Х, ряд распределения которой представлен следующей таблицей:
Х |
x1 |
x2 |
… |
xn |
P |
p1 |
p2 |
|
pn |
Математическим ожиданием дискретной случайной величины называется сумма произведений ее возможных значений на соответствующие вероятности:
![]() .
.
Математическое ожидание иногда называют просто средним значением случайной величины. Математическое ожидание определяет местоположение случайной величины на числовой оси, является так называемой «характеристикой положения».
Задача. Найти математическое ожидание числа очков, выпадающих при подбрасывании игральной кости.
Решение. Ряд распределения с.в. Х – число очков, выпадающих при подбрасывании игральной кости имеет вид:
Х |
1 |
2 |
3 |
4 |
5 |
6 |
P |
|
|
|
|
|
|
![]() .
.
Свойства математического ожидания
Математическое ожидание постоянной случайной величины равно самой величине, т.е. если с=const, то M(с)=с.
В самом деле, ряд распределения постоянной случайной величины таков:
Х |
с |
с |
… |
с |
P |
p1 |
p2 |
|
pn |
![]() .
.
Математическое ожидание суммы двух независимых случайных величин равно сумме математических ожиданий этих величин. Здесь под независимыми случайными величинами будем понимать такие случайные величины, что закон распределения одной величины не зависит от того, какое значение принимает другая случайная величина.
Учтем, что суммой двух независимых случайных величин является случайная величина, возможные значения которой равны суммам возможных значений случайных величин – слагаемых, а вероятности их - произведению вероятностей возможных значений слагаемых. Формулу М(X + Y) = М(X) + М(Y) можно доказать, непосредственно сравнивая вычисленные по определению М(X +Y) и М(X) + М(Y).
Допустим, что законы распределения Х и Y имеют вид:
Х |
х1 |
х2 |
P |
р 1 |
p2 |
Y |
у1 |
у2 |
P |
q1 |
q2 |
Тогда закон распределения Х + Y представляется так:
Х+Y |
х1+ у1 |
х1+ у2 |
х2 + у1 |
х2 + у2 |
P |
р1q1 |
p1 q2 |
p2 q1 |
p2 q2 |
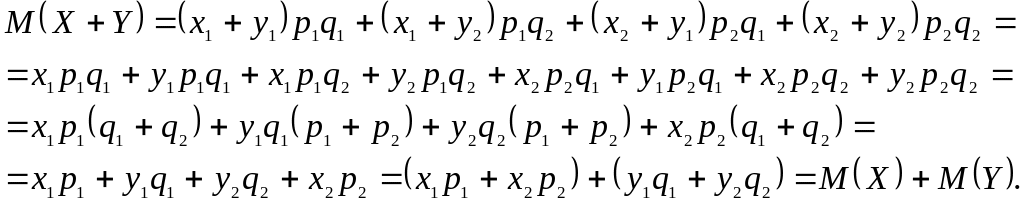
Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин: М(XY) = М(X) М(Y).
Произведением двух независимых случайных величин является случайная величина, возможные значения которой равны произведениям возможных значений случайных величин – сомножителей, а вероятности их – произведению вероятностей возможных значений сомножителей.
Замечание: Свойства 2 и 3 можно распространить на любое число случайных величин.
Постоянный сомножитель можно выносить за знак математического ожидания: М(сх) = сМ(х), если с = const..
Математическое ожидание числа появлений события в одном испытании равно вероятности этого события.
В самом деле, ряд распределения случайной величины Х – числа появления события в одном испытании имеет вид:
Х |
0 |
1 |
P |
1 – р |
p |
Очевидно, что М(х) = р.
Математическое ожидание числа появлений события в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в одном испытании, при условии, что вероятность появления события в каждом испытании одинакова, т.е. M(x)=np.
В с.д., пусть Х – число появлений события в n независимых испытаниях, оно складывается из числа появления события в отдельных испытаниях:
Х = Х1 + Х2 + … + Хn,
где Хi – число появлений события в i-том испытании. В этом случае М(Х) = М(Х1 + Х2 + … + Хn) = М(Х1) + М(Х2)+ … + М(Хn) = nМ(Х1) = = np.
Таким образом, доказан факт: математическое ожидание частоты появления события в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в одном испытании, при условии, что вероятность появления события в каждом испытании одинакова.
До сих пор рассматривалось математическое ожидание дискретной случайной величины и его свойства. Для непрерывной случайной величины Х математическое ожидание выражается не суммой, а интегралом:
![]() ,
,
где р(x) – плотность распределения величины Х.
Свойства 1 – 4 математического ожидания дискретной случайной величины естественным образом распространяются и на непрерывные с.в.
