28. Числовые характеристики составляющих системы двух случайных величин. Условное математическое ожидание

Составляющие системы случайных величин (Х, Y) являются одномерными случайными величинами. Их можно охарактеризовать численно обычным образом через математические ожидания, дисперсии, средние квадратические отклонения.

В частности, для составляющих непрерывной системы двух случайных величин (Х, Y) справедливы следующие формулы:

,

Аналогично

,

.

Важной характеристикой условного распределения является условное математическое ожидание. Ниже приведены определения условного математического ожидания составляющей дискретной и непрерывной случайной величины.

Условные математические ожидания составляющих системы двух дискретных случайных величин	Условные математические ожидания составляющей системы двух непрерывных случайных величин

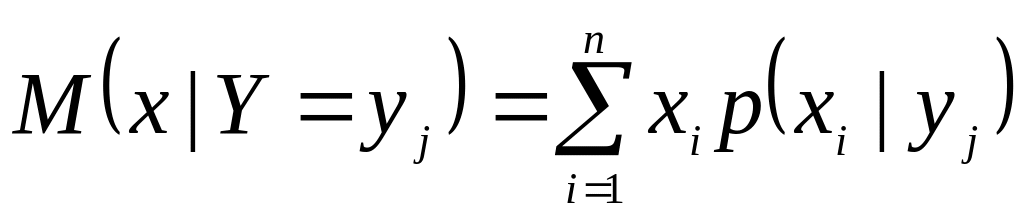
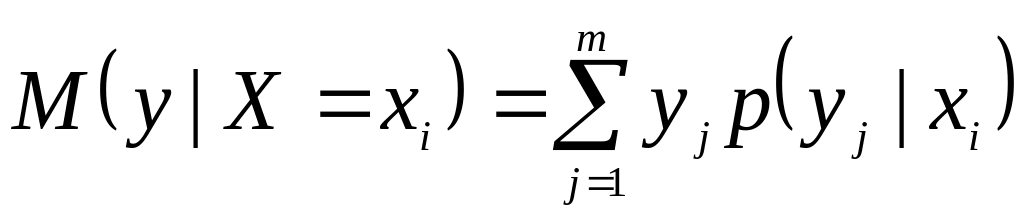
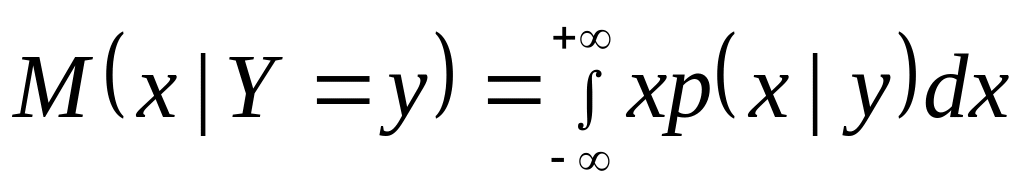
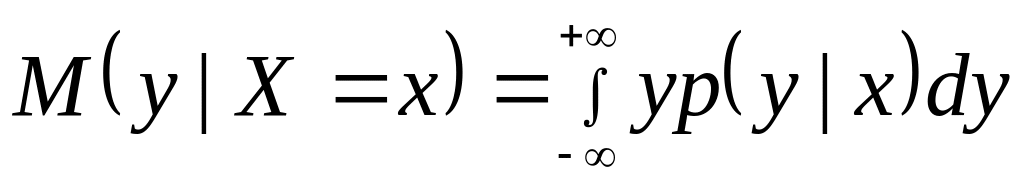
Условное математическое ожидание является функцией у, которую называют функцией регрессии х на у. Аналогично, условное математическое ожидание называется функцией регрессии у на х.

Задача. Найти условное математическое ожидание составляющей Х при условии, что составляющая Y приняла значение у=2.

Х Y	1	2	3	4
2	0,1	0,05	0,2	0,05
4	0,2	0,15	0,1	0,15

Решение.

Ранее было показано, что после того, как составляющая Y приняла значение 2, закон распределения Х представляется так:

Х	2	4
Р	0,25	0,75

. Для сравнения: безусловное математическое ожидание составляющей Х равно 3,2.

29. Корреляционный момент. Коэффициент корреляции

Для описания системы двух случайных величин кроме математических ожиданий и дисперсий составляющих используют и другие числовые характеристики. К их числу относится корреляционный момент и коэффициент корреляции.

Корреляционным моментом случайных величин Х и Y называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий:

.

Можно доказать, что

.

Система двух случайных величин	Формула для вычисления
Дискретная
Непрерывная

Корреляционный момент является характеристикой связи между случайными величинами Х и Y.

Свойства корреляционного момента

1. Если величины Х и Y независимы, то =0.

Докажем этот факт. Поскольку величины Х и Y независимы, то их отклонения от своих математических ожиданий, также независимые величины. В этом случае по свойствам мат. ожидания заключаем, что

2. 

Из определения корреляционного момента следует, что он имеет размерность, равную произведению размерностей величин Х и Y. Это затрудняет сравнение корреляционных моментов величин, имеющих разные размерности. Для устранения этого недостатка вводят безразмерную величину, называемую коэффициентом корреляции:

.

Свойства коэффициента корреляции

1. Если величины Х и Y независимы, то 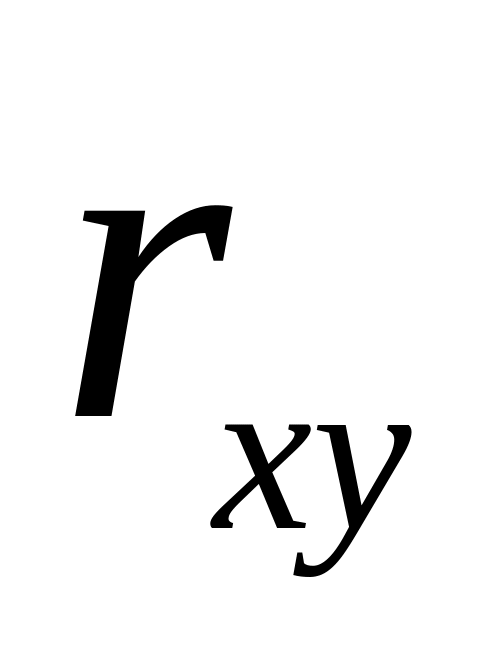=0.

2. .

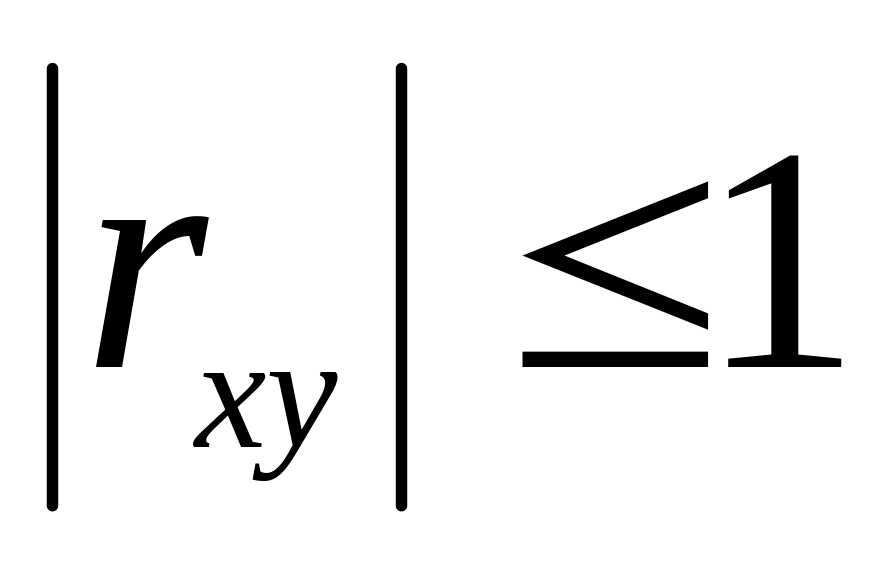Оба свойства коэффициента корреляции основываются на определении коэффициента корреляции и соответствующих свойствам корреляционного момента