32.Знакоперемен ряды, абсол и условная сходимости

Числовой ряд, содержащий бесконечное количество как положительных, так и отрицательных членов, расположенных в совершенно произвольном порядке, называется знакопеременным.

Если сходится не только данный знакопеременный ряд 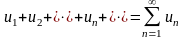(47), но и ряд 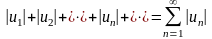(48) из модулей членов исходного ряда, то ряд (47) называется абсолютно сходящимся. Если же сам ряд (47) сходится, а ряд (48) расходится, то знакопеременный ряд (47) называется условно или неабсолютно сходящимся рядом.

33.Теорема Коши об абсол сход знакоперем ряда

Теорема 10 (теорема Коши). Из сходимости ряда (48) следует сходимость ряда (47).

Доказательство. Рассмотрим в отдельности положительные члены ряда (47) и абсолютные величины его отрицательных членов, при этом для них введём обозначения 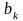и 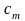. Перенумеруем и в том порядке, в котором они встречаются в ряде (47). Теперь составим два положительных ряда

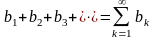, (49)

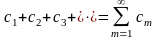. (50)

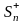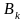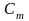Через и обозначим, соответственно, частичные суммы рядов (47) и (48). Через и обозначим те частичные суммы рядов (49) и (50), индексы которых удовлетворяют неравенствам 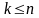, 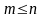(при этом 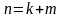). Тогда очевидны равенства

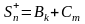, (51) . (52)

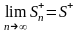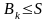По условию теоремы ряд (48) сходится. Тогда существует конечный предел . Из (52) следует, что и 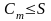. При этом положительные суммы и монотонно возрастают. Следовательно, существуют конечные пределы 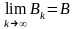, , т.е. ряды (49) и (50) сходятся (отметим, что ).

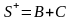Перейдём теперь к пределу в равенстве (51). Только что было установлено существование конечных пределов величин, стоящих справа. Следовательно, существует конечный предел . При этом

.

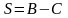34.Признак Лейбница знакочеред рядов

Если члены знакочередующегося ряда 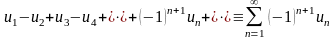(40) монотонно убывают по абсолютной величине (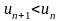 для всех n) и стремятся к нулю (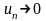 при ), то ряд сходится.

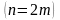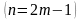Доказательство. Согласно определению 3 нужно доказать, что . Это равенство будет доказано, если его установим как при чётном n , так и при нечётном ; при этом .

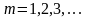Рассмотрим сначала чётную частичную сумму, т.е. сумму 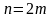первых членов ряда (40). Очевидно, что её можно записать в виде

.

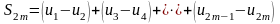Из условия теоремы следует, что все выражения в скобках этой суммы положительны. Следовательно, сама эта сумма положительна . С возрастанием номера 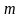эта сумма увеличится, т.к. добавится ещё одно положительное слагаемое. Теперь эту сумму запишем так:

.

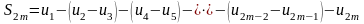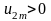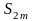В этой записи все выражения в скобках положительны и . Таким образом, получается вычитанием из 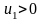некоторого количества положительных чисел. Следовательно, 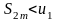при любом .

Таким образом, установлено, что последовательность чётных частичных сумм ряда возрастает и ограничена сверху. По признаку существования предела монотонной последовательности она имеет конечный предел, который обозначим S:

.

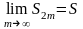Проверим теперь, что и частичные сумы с нечётными номерами сходятся к тому же числу S. Очевидно, что для таких сумм справедливо равенство 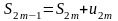. Перейдём в этом равенстве к пределу, когда 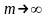. Так как по условию теоремы 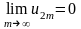, то получим следующее:

.

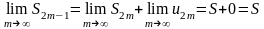Объединяя результаты 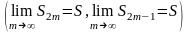, можно записать , т.е. ряд сходится. Теорема доказана.

Ряд 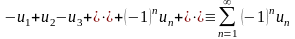(41) получается из ряда (40) умножением его на(-1). Тогда при выполнении условий теоремы 9 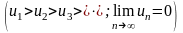этот ряд также сходится.

Знакочередующиеся ряды (40) и (41) при выполнении двух условий признака Лейбница ( для всех , ) называют рядами лейбницевского типа. Как только что было установлено, любой ряд лейбницевского типа сходится.