
- •1. Первообразная и ее свойства
- •3. Таблица интегралов.
- •2.Неопределенный интеграл и его свойства
- •4.Замена переменной в неопределенном интеграле
- •5. Интегрирование по частям в не опред. Интеграле
- •6. Интегрирование выраж содержащ квадратный трехчлен
- •7.Интегрирование простых правильных дробей
- •9.Интегрирование некоторых классов иррац функций
- •10.Интегрирование тригонометрических выражений
- •11. Определение определенного интеграла и его св-ва
- •12. Интеграл с переменным верхним пределом;производная по верхнему пределу
- •13.Формула Ньютона-Лейбница
- •14.Замена переменной в определенном интеграле
- •15.Интегрирование по частям в определенном интеграле
- •16.Геометрические приложения определенного интеграла
- •17.Несобственные интегралы по бесконечному промежутку интегрир от непрерывных функций.
- •18.Несобственные интегралы по конечному промежутку интегрирования от неограниченных функций.
- •19. Диффер уравн: опред, решение уравн, задача Коши, общ и частн решения, геом смысл решений
- •20.Диффер уравнен первого порядка с разделенными и разделяющ переменными
- •21.Лин диффер уравнения 1го порядка(методы Бернулли и Лагранжа, их решения)
- •22.Лин диффер уравн 2го порядка с пост коэфф, структура их общ решения
- •23. Структура решения лин неоднор дифф уравн 2го порядка
- •24.Нахождение частных реш лин неоднор диффер уравн 2го порядка с пост коэфф по виду правой части
- •25. Числовой ряд и его сумма; сход и расход ряды
- •26. Геометрический и гармонический ряды
- •27. Необходимые условия сходимости ряда
- •28.Полож ряды; признаки сравнен их сходимости
- •29.Предельный признак Даламбера
- •30.Предельный признак Коши
- •31.Интегральный признак Маклорена-Коши
- •32.Знакоперемен ряды, абсол и условная сходимости
- •33.Теорема Коши об абсол сход знакоперем ряда
- •34.Признак Лейбница знакочеред рядов
- •35.Теорема Абеля сходимости степенного ряда
- •36.Радиус сходим степенного ряда и его нахождение
- •37. Понятие о рядах Тейлора и Маклорена
- •39.Разложение в ряд Маклорена ф-ции cos X, sin X
26. Геометрический и гармонический ряды
Геометрический ряд – это ряд вида
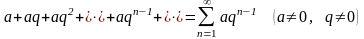 (10)составленный
из членов геометрической прогрессии.
Сумма первых
членов геометрической прогрессии при
(10)составленный
из членов геометрической прогрессии.
Сумма первых
членов геометрической прогрессии при
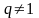 находится по формуле (2). Предел этой
суммы преобразуем к виду
находится по формуле (2). Предел этой
суммы преобразуем к виду
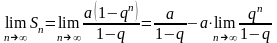 .
.
Возможны
следующие случаи в зависимости от
величины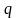 :
:
Если
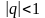 ,
то
,
то
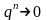 при
при
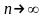 .
Поэтому
.
Поэтому
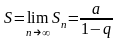 и ряд (10) сходится.
и ряд (10) сходится.
Если
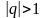 ,
то
,
то
 при
при
![]() .
Поэтому
.
Поэтому
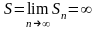 и ряд (10) расходится.
и ряд (10) расходится.
Пусть
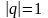 .Тогда
при
.Тогда
при
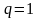 ряд (10) примет вид
ряд (10) примет вид
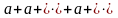 .
Для него
.
Для него
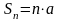 и
,
т.е. ряд (10) расходится. При
и
,
т.е. ряд (10) расходится. При
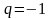 ряд (10) примет вид
ряд (10) примет вид
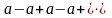 .
Для него
.
Для него
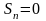 при чётном
и
при чётном
и
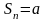 при нечётном
.
Следовательно,
при нечётном
.
Следовательно,
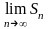 не существует; ряд (10) расходится.
не существует; ряд (10) расходится.
Можно
сделать вывод, что геометрический ряд
сходится при
и расходится при
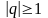 .
.
В
связи с введением суммы ряда всякое
действительное число
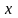 ,
представленное в виде бесконечной
десятичной дроби
,
представленное в виде бесконечной
десятичной дроби
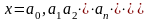 ,можно
понимать как сумму ряда
,можно
понимать как сумму ряда
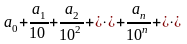 ,частичными
суммами которого являются десятичные
приближения
,частичными
суммами которого являются десятичные
приближения
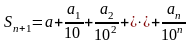 этого
числа
по недостатку.
этого
числа
по недостатку.
Сказанное
позволит представлять в виде обыкновенных
дробей бесконечные десятичные
периодические дроби. При этом будет
применена формула 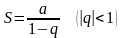 (11)
нахождения суммы
(11)
нахождения суммы
 геометрического ряда.
геометрического ряда.
Числовой
ряд с общим членом
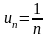 называется гармоническим
и имеет вид
называется гармоническим
и имеет вид
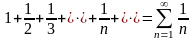 .Каждый
член этого ряда, начиная со второго,
представляет собой среднее гармоническое
двух соседних его членов. Число C
называется средним гармоническим чисел
a
и b,
если выполняется равенство
.Каждый
член этого ряда, начиная со второго,
представляет собой среднее гармоническое
двух соседних его членов. Число C
называется средним гармоническим чисел
a
и b,
если выполняется равенство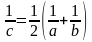 .
.
Так
как его
-я
частичная сумма
 представима
в виде
представима
в виде
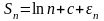 (4)при этом
(4)при этом
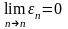 ),
то
),
то
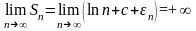 и, следовательно, этот ряд расходится.
Ввиду того, что доказательство равенства
(4) трудное, приведём более простое
доказательство расходимости ряда
и, следовательно, этот ряд расходится.
Ввиду того, что доказательство равенства
(4) трудное, приведём более простое
доказательство расходимости ряда
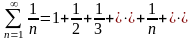 .
.
Сначала получим некоторое вспомогательное неравенство. Так как
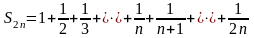 ,
,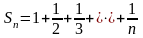 ,
,
то
разность
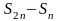 имеет вид
имеет вид
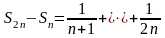 .Заменив
в этом равенстве, содержащем n
слагаемых, каждое слагаемое наименьшим,
равным
.Заменив
в этом равенстве, содержащем n
слагаемых, каждое слагаемое наименьшим,
равным
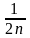 ,
получим вспомогательное неравенство
,
получим вспомогательное неравенство
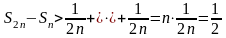 или
или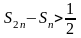 .
.
Предположим
противное, т.е. что гармонический ряд
сходится. Тогда
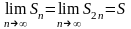 .
Переходя к пределу в последнем
неравенстве, получим, что
.
Переходя к пределу в последнем
неравенстве, получим, что
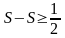 или
или
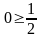 .
.
Получили противоречие. Следовательно, предположение о сходимости гармонического ряда неверно, т.е. гармонический ряд расходится.
Ряд вида
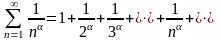 , (13)
, (13)
где
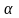 – любое вещественное число, называется
обобщённым
гармоническим рядом.
Он сходится при
– любое вещественное число, называется
обобщённым
гармоническим рядом.
Он сходится при
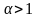 ,
расходится при
,
расходится при
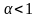 .
Это будет установлено в дальнейшем.
При
.
Это будет установлено в дальнейшем.
При
 ряд (13) является гармоническим и,
следовательно, расходится.
ряд (13) является гармоническим и,
следовательно, расходится.
27. Необходимые условия сходимости ряда
Теорема
1.
Если ряд
(6)
сходится, то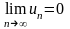 .(14)Доказательство.
Так как ряд (6) по условию теоремы
сходится, то
.(14)Доказательство.
Так как ряд (6) по условию теоремы
сходится, то
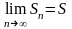 .
Очевидно, что
.
Очевидно, что
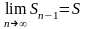 (
(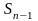 пробегает ту же последовательность
чисел, что и
).
Так как
пробегает ту же последовательность
чисел, что и
).
Так как
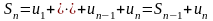 ,то
при
,то
при
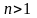 имеем равенство
имеем равенство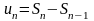 .
.
Переходя
в этом равенстве к пределу, получим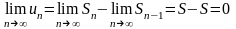 ,
,
что и требовалось доказать.
Обратная
теорема к теореме 1, вообще говоря,
неверна. Условие (14) есть лишь необходимое
условие сходимости ряда, но не является
достаточным. Из того, что выполняется
(14), не следует, что ряд сходится. При
выполнении условия (14) ряд может как
сходиться, так и расходиться. Примером
расходящегося ряда, для которого
выполнено условие (14), является
рассмотренный в предыдущем пункте
гармонический ряд
(12) (очевидно, что
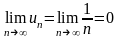 ).
).
У сходящихся рядов, рассмотренных ранее, необходимое условие их сходимости было выполнено.
С
другой стороны, если условие (14) не
выполнено (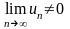 или этот предел не существует), то ряд
расходится.
или этот предел не существует), то ряд
расходится.
К
расходящимся рядам относятся, например,
ряды со следующими общими членами:
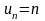 ,
,
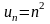 ,
,
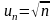 ,
,
 ,
,
 .
.
При
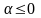 обобщённый гармонический ряд (13)
расходится, так как при любых таких
его общий член
обобщённый гармонический ряд (13)
расходится, так как при любых таких
его общий член
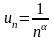 не стремится к нулю.
не стремится к нулю.
Рассмотрим
обобщённый гармонический ряд (13) при
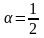 ,
т.е. ряд
,
т.е. ряд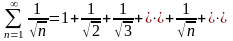 .
.
Необходимое
условие (14) выполнено, т.к.
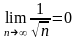 .
Для его n-й
частичной суммы, начиная со второй,
выполняется неравенство
.
Для его n-й
частичной суммы, начиная со второй,
выполняется неравенство
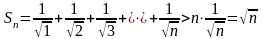 ,
,
из которого следует, что увеличивается до бесконечности вместе с увеличением номера . Согласно определению 3 данный ряд расходится, хотя необходимое условие сходимости выполнено.
По
аналогии с этим простым случаем
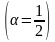 докажем, что ряд
(13) расходится при всех
,
удовлетворяющих двойному неравенству
докажем, что ряд
(13) расходится при всех
,
удовлетворяющих двойному неравенству
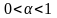 .
Отметим, что для таких
необходимое условие (14) выполнено.
.
Отметим, что для таких
необходимое условие (14) выполнено.
Так как все члены частичной суммы
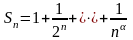 этого
ряда не меньше чем
этого
ряда не меньше чем
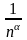 и она состоит из
членов,
то
и она состоит из
членов,
то
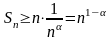 .
.
Перейдём
к пределу в этом неравенстве с учётом
того, что при
число
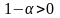 .
Получим следующее:
.
Получим следующее:
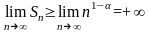 .Следовательно,
.Следовательно,
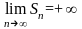 ;
ряд (13) при таких
расходится.
;
ряд (13) при таких
расходится.
