
- •1. Первообразная и ее свойства
- •3. Таблица интегралов.
- •2.Неопределенный интеграл и его свойства
- •4.Замена переменной в неопределенном интеграле
- •5. Интегрирование по частям в не опред. Интеграле
- •6. Интегрирование выраж содержащ квадратный трехчлен
- •7.Интегрирование простых правильных дробей
- •9.Интегрирование некоторых классов иррац функций
- •10.Интегрирование тригонометрических выражений
- •11. Определение определенного интеграла и его св-ва
- •12. Интеграл с переменным верхним пределом;производная по верхнему пределу
- •13.Формула Ньютона-Лейбница
- •14.Замена переменной в определенном интеграле
- •15.Интегрирование по частям в определенном интеграле
- •16.Геометрические приложения определенного интеграла
- •17.Несобственные интегралы по бесконечному промежутку интегрир от непрерывных функций.
- •18.Несобственные интегралы по конечному промежутку интегрирования от неограниченных функций.
- •19. Диффер уравн: опред, решение уравн, задача Коши, общ и частн решения, геом смысл решений
- •20.Диффер уравнен первого порядка с разделенными и разделяющ переменными
- •21.Лин диффер уравнения 1го порядка(методы Бернулли и Лагранжа, их решения)
- •22.Лин диффер уравн 2го порядка с пост коэфф, структура их общ решения
- •23. Структура решения лин неоднор дифф уравн 2го порядка
- •24.Нахождение частных реш лин неоднор диффер уравн 2го порядка с пост коэфф по виду правой части
- •25. Числовой ряд и его сумма; сход и расход ряды
- •26. Геометрический и гармонический ряды
- •27. Необходимые условия сходимости ряда
- •28.Полож ряды; признаки сравнен их сходимости
- •29.Предельный признак Даламбера
- •30.Предельный признак Коши
- •31.Интегральный признак Маклорена-Коши
- •32.Знакоперемен ряды, абсол и условная сходимости
- •33.Теорема Коши об абсол сход знакоперем ряда
- •34.Признак Лейбница знакочеред рядов
- •35.Теорема Абеля сходимости степенного ряда
- •36.Радиус сходим степенного ряда и его нахождение
- •37. Понятие о рядах Тейлора и Маклорена
- •39.Разложение в ряд Маклорена ф-ции cos X, sin X
35.Теорема Абеля сходимости степенного ряда
Для
степенного ряда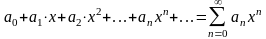 (24) имеют место следующие утверждения:
(24) имеют место следующие утверждения:
1)
если степенной ряд (24) сходится при
 ,
то он сходится (притом абсолютно) при
всех
таких, что
,
то он сходится (притом абсолютно) при
всех
таких, что
 ;
;
2)
если ряд расходится при
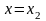 ,
то он расходится при всех
,
для которых
,
то он расходится при всех
,
для которых
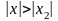 .
.
Доказательство.
1. По условию теоремы числовой ряд
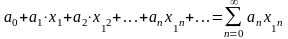 (27) сходится. Следовательно, по необходимому
признаку сходимости
(27) сходится. Следовательно, по необходимому
признаку сходимости
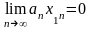 .
Отсюда следует, что сходящаяся числовая
последовательность
.
Отсюда следует, что сходящаяся числовая
последовательность
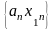 ограничена, т.е. найдётся такое число
ограничена, т.е. найдётся такое число
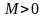 ,
что для всех
будет выполняться неравенство
,
что для всех
будет выполняться неравенство
 .
.
Пусть
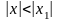 ,
тогда величина
,
тогда величина
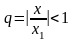 и, следовательно,
и, следовательно,
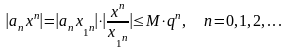 ,
т.е. модуль каждого члена ряда (24) не
превосходит соответствующего члена
сходящегося геометрического ряда
,
т.е. модуль каждого члена ряда (24) не
превосходит соответствующего члена
сходящегося геометрического ряда
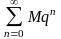
 .
Поэтому, по первому признаку сравнения
будет сходиться ряд
.
Поэтому, по первому признаку сравнения
будет сходиться ряд
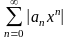 .
Следовательно, при
ряд (24) сходится абсолютно.
.
Следовательно, при
ряд (24) сходится абсолютно.
2.
Дано, что ряд расходится в точке
;
нужно доказать, что он расходится для
всех x,
удовлетворяющих неравенству
.
Предположим противное: при некотором
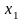 ,
удовлетворяющем неравенству
,
удовлетворяющем неравенству
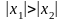 ,
степенной ряд сходится. Тогда по первой
части теоремы Абеля ряд будет сходиться
при всех
,
для которых
,
и, в частности, в точке
,
степенной ряд сходится. Тогда по первой
части теоремы Абеля ряд будет сходиться
при всех
,
для которых
,
и, в частности, в точке
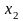
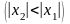 ,
что противоречит условию теоремы.
,
что противоречит условию теоремы.
С геометрической точки зрения в теореме Абеля утверждается следующее:
1)
если ряд (24) сходится в точке
 ,
то он абсолютно сходится на интервале
,
то он абсолютно сходится на интервале
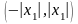 ;
;
2)
если ряд (24) расходится в точке
,
то он расходится на луче
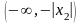 ,
лежащем левее точки
,
лежащем левее точки
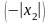 ,
и на луче
,
и на луче
 ,
лежащем правее точки
,
лежащем правее точки
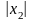
36.Радиус сходим степенного ряда и его нахождение
Число
R
называется радиусом
сходимости степенного ряда
(24). Промежуток
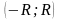 называется интервалом
сходимости степенного ряда
(24).
называется интервалом
сходимости степенного ряда
(24).
В
упоминавшейся ситуации 1) считают, что
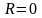 (ряд (24) сходится лишь при
(ряд (24) сходится лишь при
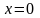 );
в ситуации 2) полагают
);
в ситуации 2) полагают
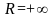 .
Следовательно, можно считать, что радиус
сходимости удовлетворяет неравенствам
.
Следовательно, можно считать, что радиус
сходимости удовлетворяет неравенствам
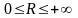 .
.
Остался
открытым вопрос о сходимости степенного
ряда (24) на концах интервала
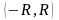 ,
то есть в точках
,
то есть в точках
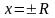 .
Общего ответа о сходимости ряда в этих
точках дать нельзя. В этих точках
возможны следующие случаи: 1) ряд
расходится в обеих точках; 2) ряд сходится
в обеих точках (в этом случае область
сходимости ряда обращается в замкнутый
промежуток
.
Общего ответа о сходимости ряда в этих
точках дать нельзя. В этих точках
возможны следующие случаи: 1) ряд
расходится в обеих точках; 2) ряд сходится
в обеих точках (в этом случае область
сходимости ряда обращается в замкнутый
промежуток
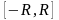 ;
3) ряд сходится в одной из точек
и расходится в другой. В каждом конкретном
примере надо проводить отдельное
исследование поведения степенного
ряда на концах интервала
.
;
3) ряд сходится в одной из точек
и расходится в другой. В каждом конкретном
примере надо проводить отдельное
исследование поведения степенного
ряда на концах интервала
.
Для
отыскания интервала сходимости можно
использовать признаки Даламбера или
Коши, применённые к ряду, составленному
из абсолютных величин членов степенного
ряда (24) или
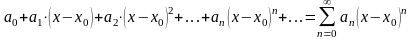 (25), т.е. к ряду
(25), т.е. к ряду
или
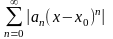 .
.
Для вычисления радиуса сходимости R степенного ряда можно использовать такие формулы:
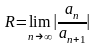 ,
(28)
,
(28)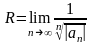 .(29)
.(29)
Они являются следствиями применения признаков Даламбера и Коши при отыскании интервала сходимости
37. Понятие о рядах Тейлора и Маклорена
Ряд
вида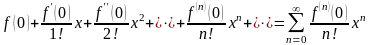 (37)
(37)
называется
рядом Маклорена
функции
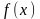 .
.
Такой ряд можно образовать для любой бесконечно дифференцируемой функции в точке . Ряд (37) есть степенной ряд по степеням переменной ; его коэффициенты называют коэффициентами Маклорена.
Ряд вида
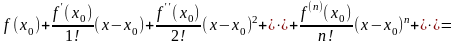
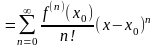 (38)
(38)
называется рядом Тейлора функции .
Ряд
(38) является степенным рядом по степеням
двучлена
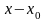 и может быть образован для любой
бесконечно дифференцируемой функции
в точке
и может быть образован для любой
бесконечно дифференцируемой функции
в точке
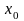 .
Его коэффициенты называются коэффициентами
Тейлора.
.
Его коэффициенты называются коэффициентами
Тейлора.
Ряды (37) и (38) имеют данное название независимо от того, в какой области они сходятся и является ли функция , которая задаёт коэффициенты этих рядов, их суммой.
Ряд
(37) является частным случаем ряда (38)
((37) получается из (38) при
 )
)
38.разложение в ряд Маклорена ex и ln(1+x)



