20.Диффер уравнен первого порядка с разделенными и разделяющ переменными

Дифференциальным уравнением с разделёнными переменными называется уравнение вида

f₁(y)dy = f₂(x)dx, (2.1) которое записано в дифференциальной форме. Здесь f₁(y), f₂(x) – известные непрерывные функции своих аргументов. Переменные х и у разделены, поскольку в уравнении (2.1) левая часть содержит лишь переменную у и её дифференциал, а правая часть – только переменную х и её дифференциал.

Соотношение вида 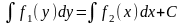(2.2)

является общим интегралом дифференциального уравнения с разделёнными переменными.

Пример. Найти решение дифференциального уравнения

.Решение. Так как переменные разделены, то

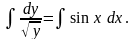
Найдя интегралы, имеем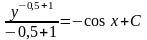 или 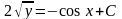.Тогда у = ( – 0,5cos x + 0,5C)².

Дифференциальным уравнением с разделяющимися переменными называется уравнение вида f₁(x)q₁(y)dy = f₂(x)q₂(y)dx. (2.3)

С помощью деления на f₁(x)q₂(y) ≠ 0 уравнение (2.3) приводится к виду 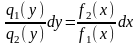, интегрируя которое находим общий интеграл дифференциального уравнения «в квадратурах» 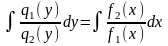. (2.4)

Отметим, что при делении возможна потеря частных решений.

Пример. Найти решение дифференциального уравнения

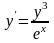. Решение. Учитывая, что , имеем 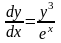, откуда 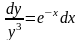. Интегрируя это равенство, получим следующее:

Тогда 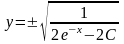. Надо добавить ещё потерянное при делении решение у = 0.

21.Лин диффер уравнения 1го порядка(методы Бернулли и Лагранжа, их решения)

Линейным дифференциальным уравнением первого порядка называется уравнение, в которое неизвестная функция и её первая производная входят в первой степени:

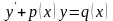. (5.1)

Существуют два метода решения уравнения (5.1): метод Бернулли (метод подстановки) и метод Лагранжа (метод вариации произвольной постоянной).

Метод Бернулли (метод подстановки)

Решение уравнения (5.1) ищется в виде y = uv,(5.2)

т.е. в виде произведения двух неизвестных дифференцируемых функций u = u(x) и v = v(x). Подставляя функцию (5.2) и её производную

y′ = u′v + uv′ в уравнение (5.1), в результате получим:

u′v + u[v′ + p(x)v] = q(x).(5.3)

Подберём какую-нибудь функцию v, чтобы выражение в квадратных скобках последнего равенства равнялось нулю: v′ + p(x)v = 0. (5.4)

Разделяя в (5.4) переменные и интегрируя, получим .

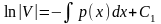Так как нам нужно иметь одну из функций v, удовлетворяющих (5.4), то можно положить С₁ = 0. Тогда 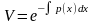. (5.5)

Подставим найденную функцию v(x) в (5.3). В результате приходим к дифференциальному уравнению 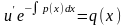(5.6)

с разделяющимися переменными относительно другой неизвестной функции u(x). Решением уравнения (5.6) является функция 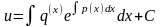, (5.7) где С – произвольная постоянная.

Подставляя найденные функции u и v (см. (5.5) и (5.7)) в равенство (5.2), получаем общее решение дифференциального уравнения (5.1) в следующем виде: 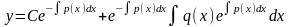. (5.8)

Однако при решении конкретных примеров не рекомендуется использовать равенство (5.8). Обычно действуют по изложенной выше схеме.

Метод Лагранжа (метод вариации произвольной постоянной)

Алгоритм метода

1. Для заданного неоднородного уравнения (5.1) выписывается соответствующее ему так называемое приведённое однородное уравнение вида (5.9), т.е. правая часть f(x) уравнения (5.1) заменяется нулём, а коэффициент р(х) при неизвестной функции y(x) сохраняется.

2. Методом разделения переменных находится общее решение этого однородного уравнения, которое имеет вид (5.10).

3. В (5.10) постоянную С заменяют на неизвестную функцию С(х), т.е. полагают С = С(х). При этом говорят, что постоянную С варьируют (изменяют). Таким образом, решение исходного неоднородного уравнения (5.1) ищут в виде 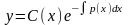, (5.11) при этом С(х) подлежит найти.

4. Функцию (5.11) дифференцируют, а затем её и её производную подставляют в уравнение (5.1).

5. После этих действий получится следующее уравнение для нахождения С(х):

.

6. Из последнего дифференциального уравнения находится путём разделения переменных неизвестная функция С(х): 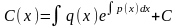. (5.12)

7. Функция (5.12) подставляется в равенство (5.11). Получится общее решение неоднородного уравнения (5.1) в виде (5.8).

в конкретных примерах нецелесообразно применять громоздкую и трудно запоминающуюся формулу (5.8). Обычно каждый раз повторяют все действия приведённого алгоритма.

Метод Бернулли и метод Лагранжа приводят к одному и тому же результату (5.8).

Метод вариации позволяет выявить структуру общего решения неоднородного уравнения (5.1). Из формулы (5.8) видно, что общее решение линейного неоднородного дифференциального уравнения первого порядка (5.1) равно сумме общего решения соответствующего приведённого однородного уравнения, которое имеет вид (5.10), и частного решения 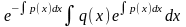самого неоднородного уравнения (5.1), получающегося из его общего решения (5.8) при С=0.