
- •1. Первообразная и ее свойства
- •3. Таблица интегралов.
- •2.Неопределенный интеграл и его свойства
- •4.Замена переменной в неопределенном интеграле
- •5. Интегрирование по частям в не опред. Интеграле
- •6. Интегрирование выраж содержащ квадратный трехчлен
- •7.Интегрирование простых правильных дробей
- •9.Интегрирование некоторых классов иррац функций
- •10.Интегрирование тригонометрических выражений
- •11. Определение определенного интеграла и его св-ва
- •12. Интеграл с переменным верхним пределом;производная по верхнему пределу
- •13.Формула Ньютона-Лейбница
- •14.Замена переменной в определенном интеграле
- •15.Интегрирование по частям в определенном интеграле
- •16.Геометрические приложения определенного интеграла
- •17.Несобственные интегралы по бесконечному промежутку интегрир от непрерывных функций.
- •18.Несобственные интегралы по конечному промежутку интегрирования от неограниченных функций.
- •19. Диффер уравн: опред, решение уравн, задача Коши, общ и частн решения, геом смысл решений
- •20.Диффер уравнен первого порядка с разделенными и разделяющ переменными
- •21.Лин диффер уравнения 1го порядка(методы Бернулли и Лагранжа, их решения)
- •22.Лин диффер уравн 2го порядка с пост коэфф, структура их общ решения
- •23. Структура решения лин неоднор дифф уравн 2го порядка
- •24.Нахождение частных реш лин неоднор диффер уравн 2го порядка с пост коэфф по виду правой части
- •25. Числовой ряд и его сумма; сход и расход ряды
- •26. Геометрический и гармонический ряды
- •27. Необходимые условия сходимости ряда
- •28.Полож ряды; признаки сравнен их сходимости
- •29.Предельный признак Даламбера
- •30.Предельный признак Коши
- •31.Интегральный признак Маклорена-Коши
- •32.Знакоперемен ряды, абсол и условная сходимости
- •33.Теорема Коши об абсол сход знакоперем ряда
- •34.Признак Лейбница знакочеред рядов
- •35.Теорема Абеля сходимости степенного ряда
- •36.Радиус сходим степенного ряда и его нахождение
- •37. Понятие о рядах Тейлора и Маклорена
- •39.Разложение в ряд Маклорена ф-ции cos X, sin X
5. Интегрирование по частям в не опред. Интеграле
Интегрированием по частям называется нахождение интеграла по формуле
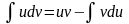 ,
,
где u(x) и v(x) - дифференцируемые функции.
Применение её целесообразно, когда интеграл в правой части формулы более прост для нахождения, нежели исходный. В некоторых случаях формулу необходимо применять несколько раз.
При этом за u(x) берётся такая функция, которая при дифференцировании упрощается, а за dv -та часть подынтегрального выражения, интеграл от которой известен или может быть найден. Так, например,
для
интегралов вида
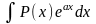 ,
,
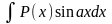 ,
,
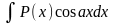
за u(x) следует принять многочлен P(x) .
Для
интегралов вида
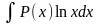 ,
,
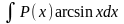 ,
,
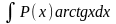
за u(x) принимаются функции lnx, arcsinx, arctgx, а за dv - выражение P(x)dx .
Т.е.![]()
Доказательство.
Пусть F1(x) и F2(x) соответственно
некоторые первообразные для ![]() и
и ![]() .
.
Тогда
по определению первообразной и
правилу дифференцирования произведения
двух функций ![]() +
=
+
=![]() ,
, ![]() .
.
Следовательно, по следствию из теоремы Лагранжа:
F1(x)
+ F2(x) = ![]() + c, где c –
некоторая константа, или F1(x) =
- F2(x).
+ c, где c –
некоторая константа, или F1(x) =
- F2(x).
Так как
![]()
из
данного равенства следует, что ![]()
Замечание: Формулу интегрирования по частям следует понимать так: множество функций {F1(x) + C1}, стоящих в левой части равенства, совпадает со множеством функций { -F2(x) + c3}, стоящих в правой части, где с3 = с – с2, а с1 и с2 – произвольные числа.
6. Интегрирование выраж содержащ квадратный трехчлен
1°. Интеграл вида
![]()
путем дополнения квадратного трехчлена до полного квадрата по формуле
![]()
сводится к одному из двух интегралов
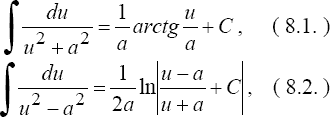
где u = х + k.
2°. Интеграл
![]()
сводится к интегралам вида (8.1) или (8.2) и интегралу
![]()
3°. Интеграл
![]()
сводится к одному из интегралов:
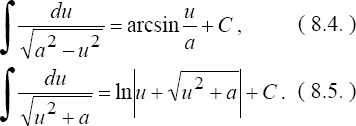
4°. Интеграл вида
![]()
сводится к одному из двух интегралов
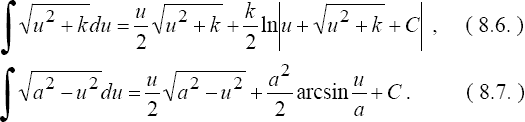
5°. Интеграл вида
![]()
сводится к разобранным выше интегралам.
7.Интегрирование простых правильных дробей
Если P(z) и Q(z) –
многочлены в комплексной области,
то ![]() -
рациональная дробь. Она называется правильной,
если степень P(z) меньше
степени Q(z),
и неправильной,
если степень Р не
меньше степени Q.
-
рациональная дробь. Она называется правильной,
если степень P(z) меньше
степени Q(z),
и неправильной,
если степень Р не
меньше степени Q.
Любую неправильную дробь можно представить в виде:
![]() ,где
P(z)
= Q(z)
S(z)
+ R(z),
a R(z)
– многочлен,
степень которого меньше степени Q(z).
,где
P(z)
= Q(z)
S(z)
+ R(z),
a R(z)
– многочлен,
степень которого меньше степени Q(z).
Таким
образом, интегрирование рациональных
дробей сводится к интегрированию
многочленов, то есть степенных функций,
и правильных дробей, так как ![]() является
правильной дробью.
является
правильной дробью.
Определение . Простейшими (или элементарными) дробями называются дроби следующих видов:
1.
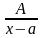 ;
;

2.
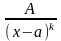 , где к -целое число, больше единицы
, где к -целое число, больше единицы
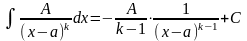
3.
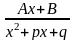 , где
, где
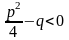 ,
т.е. квадратный трёхчлен
,
т.е. квадратный трёхчлен
 не
имеет действительных корней
не
имеет действительных корней
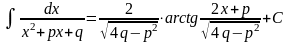
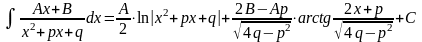
4.
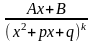
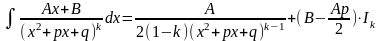
Вычисление
интеграла
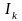 производится по рекуррентной
формуле :
производится по рекуррентной
формуле :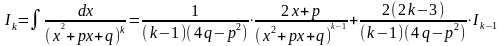
8.Разложение рациональных дробей на простейшие, интегрирование рациональных функций.
Рациональной называется функция вида
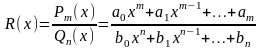
где
m,n-целые,
положительные числа. Если m<n,то
R(x)
называется правильной дробью, если
m n
,то неправильной. Всякую неправильную
дробь путём деления числителя на
знаменатель можно представить в виде
суммы некоторого многочлена и правильной
дроби:
n
,то неправильной. Всякую неправильную
дробь путём деления числителя на
знаменатель можно представить в виде
суммы некоторого многочлена и правильной
дроби:
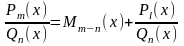 , l<n.
, l<n.
Так как всякий многочлен легко интегрируется, то интегрирование рациональных функций сводится к интегрированию правильных дробей. Всякую правильную рациональную дробь можно разложить в сумму простейших рациональных дробей.
Теорема. Правильную
рациональную дробь![]() где
где![]() можно
единственным образом разложить на
сумму простейших дробей:
можно
единственным образом разложить на
сумму простейших дробей:
![]()
![]() -
(6)
-
(6)
(A1, A2, …, Ak, B1, B2, …, B1, M1, N1, M2, M2, …, Ms, Ns – некоторые действительные числа).
Метод неопределенных коэффициентов. Суть метода неопределенных коэффициентов состоит в следующем. Пусть дано разложение правильной рациональной дроби по формуле (6) на простейшие дроби с неопределенными коэффициентами. Приведем простейшие дроби к общему знаменателю Qm(x)и приравняем многочлен, получившийся в числителе, многочлену Pn(x).
Метод частных значений. При нахождении неопределенных коэффициентов вместо того, чтобы сравнивать коэффициенты при одинаковых степенях х, можно дать переменной х несколько частных значений (по числу неопределенных коэффициентов) и получить таким образом систему уравнений относительно неопределенных коэффициентов. Особенно выгодно применять этот метод в случае, корни знаменателя рациональной дроби просты и действительны. Тогда оказывается удобным последовательно полагать равным каждому из корней знаменателя.
