17.Несобственные интегралы по бесконечному промежутку интегрир от непрерывных функций.

Определение несобственного интеграла по бесконечному промежутку. Пусть функция f(x) определена на полуоси и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла при называется несобственным интегралом функции f(x) от a до и обозначается . Итак, по определению, . Если этот предел существует и конечен, интеграл называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся.

18.Несобственные интегралы по конечному промежутку интегрирования от неограниченных функций.

Пусть на полуинтервале задана функция , интегрируемая на любом отрезке, принадлежащем данному интервалу, однако не интегрируемая на отрезке . В точке эта функция может быть вовсе не определена и стремиться к , либо вовсе не иметь никакого предела. Рассмотрим функцию . Она определена при . Эта функция может иметь предел при (левосторонний предел). Этот предел будем называть значением интеграла от по всему полуинтервалу и обозначать в точности: Определение. Пусть функция удовлетворяет указанным выше условиям на . Несобственным интегралом второго рода назовём определенный интеграл

значение которого равняется левостороннему пределу

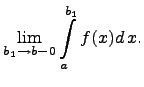
Если этот предел существует, то несобственный интеграл называется сходящимся, а если предела не существует, то расходящимся. Расходящемуся интегралу не приписывается никакого числового значения.

19. Диффер уравн: опред, решение уравн, задача Коши, общ и частн решения, геом смысл решений

Уравнение, в которое входят производные неизвестной функции, называется дифференциальным. Если эта искомая функция зависит лишь от одного аргумента, то уравнение называется обыкновенным дифференциальным уравнением. Если же неизвестная функция является функцией нескольких независимых переменных, то дифференциальное уравнение называется уравнением в частных производных.

Порядком дифференциального уравнения называется максимальный (наивысший) порядок входящей в него производной неизвестной функции.

Примерами обыкновенных дифференциальных уравнений являются уравнения с неизвестной функцией у = у(х)

1) 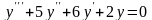; 2) ;

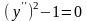3) ; 4) .

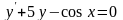При этом первое из них – третьего порядка, второе и третье – второго порядка, а четвёртое – первого порядка. Из примеров видно, что сама функция и некоторые её производные в записи уравнения могут отсутствовать (см. примеры 2 и 3), но обязательно наличие старшей производной при указанном порядке уравнения.

Примером дифференциального уравнения в частных производных является уравнение второго порядка

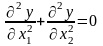
с неизвестной функцией y = y(x₁, x₂) двух переменных.

Решением дифференциального уравнения называется любая функция, при подстановке которой в уравнение (с учётом входящих в него производных) получится тождество.

Например, решением обыкновенного дифференциального уравнения первого порядка

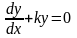является функция

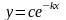, где с – произвольная постоянная. Таким образом, это уравнение имеет бесконечное множество решений.

Общий вид дифференциального уравнения первого порядка представляет собой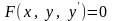 . (1.1)В равенстве (1.1) F есть известная функция трёх переменных, т.е. это соотношение связывает три переменные величины: независимую переменную х, неизвестную функцию у(х) и её производную y′(х).

В некоторых случаях уравнение (1.1) можно однозначно разрешить относительно производной у′, т.е. представить в виде у′ = f(x, y), (1.2)

где f(x,y) – конкретная функция двух переменных. Уравнение (1.2) называют дифференциальным уравнением первого порядка, разрешённым относительно производной. при условии у(х₀) = у₀, (1.5) где х0 – произвольная точка из промежутка, на котором рассматривается уравнение, а у0 – произвольно заданное число, называется частным решением (частным интегралом) дифференциального уравнения. График частного решения называют интегральной кривой. Задача нахождения решения дифференциального уравнения (1.1) или (1.2) с присоединённым к нему условием (1.5), называется задачей Коши или задачей с начальным условием.

Выделим во множестве решений y=x2 + C только что рассмотренного дифференциального уравнения y′ = 2x функцию (интегральную кривую), проходящую через точку М(1, 2), т.е. решение, удовлетворяющее условию у(1) = 2. Им будет интегральная кривая у = х2 + 1. Такое решение называется частным решением (частным интегралом) этого дифференциального уравнения. Оно получилось из решения у = х2 + С подбором постоянной С (в данной ситуации оказалось, что С = 1). Решение у = х2 + С, где С – произвольная постоянная, будет называться общим решением (общим интегралом) уравнения y′ = 2x. С геометрической точки зрения общее решение представляет собой семейство интегральных кривых (в данном случае – семейство парабол).