4.3. Решение задач конвективного теплообмена на основе теории подобия

Академик Гухман путем введения коэффициентов подобия решил эту задачу.

Определим условия подобия физических величин.

Физические явления подобны если:

1. Они одинаковы по своей физической природе (тепловому потоку подобен только тепловой поток).

2. Описываются одними и теми же уравнениями.

3. Протекают в геометрически подобных системах.

Условием геометрического подобия является пропорциональность координат:

, (4.8)

где С_l - константа подобия линейных размеров.

4. Кинематическое подобие предполагает в сходственных точках пропорциональность скоростей и ускорений:

, (4.9)

где С_w - константа подобия полей скоростей;

, (4.10)

где С_j - константа подобия полей ускорений.

5. Динамическое подобие - подобие полей действующих сил:

, (4.11)

где С_р - константа подобия полей действующих сил.

6. Условие теплового подобия – это подобие полей температур и тепловых потоков

, (4.12)

где С_T - константа подобия полей температур;

, (4.13)

где С_q - константа подобия тепловых потоков.

Если хотя бы одно условие не выполняется, явления не подобны.

При использовании теории подобия переходят к безразмерным коэффициентам.

4.4. Приведение системы дифференциальных уравнений к безразмерному виду

Предположим, что имеется два подобных явления, описываемые одними уравнениями. Следовательно, в системе

; (4.14)

; (4.15)

(4.16)

- константы подобия, входящие в данное уравнение.

Преобразуем (4.16) к следующему виду:

.(4.17)

Заменим в уравнении (4.14) все элементы соотношениями (4.17), тогда:

; (4.18)

. (4.19)

Если сопоставить (4.15) и (4.19), то получим

. (4.20)

Соотношение (4.20) называют индикатором подобия.

У подобных явлений индикаторы подобия равны единице.

В выражении (4.20), используя (4.16), сделаем обратную замену:

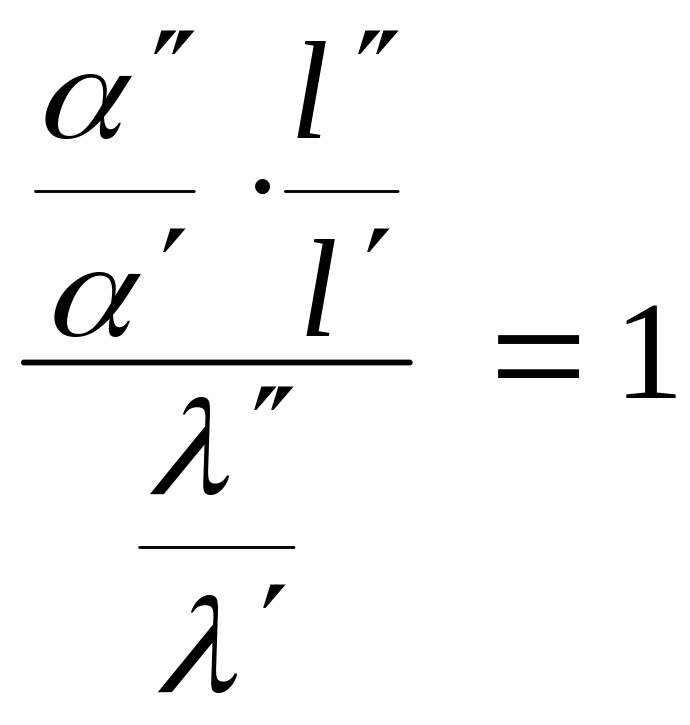. (4.21)

Оставим в левой части величины с двумя штрихами:

, (4.22)

где Nu - критерий или число Нуссельта.

Nu - это безразмерная величина, содержащая искомую величину коэффициента теплоотдачи. Эта величина для всех подобных явлений одинакова.

Из уравнения (4.5) получается:

- число гомохромности. (4.23)

- критерий Фурье. (4.24)

- критерий Пекле. (4.25)

Из уравнения (4.6) получается:

- число гомохромности. (4.26)

- критерий Фруда. (4.27)

- критерий Эйлера. (4.28)

- критерий Рейнольдса. (4.29)

Таким образом, система дифференциальных уравнений преобразована к семи критериям Nu = f (Ho, Fo, Pe, Eu, Fr, Re) - эта взаимосвязь находится экспериментально.

4.5. Теоремы подобия

Первая и вторая теоремы исходят из факта существования подобия и формулируют основные свойства подобных между собой явлений. Третья теорема, наоборот, позволяет установить признаки подобия.

Первая теорема устанавливает зависимость между константами подобия, вытекающую из наличия уравнений, описывающих механизм данного явления. Ее можно сформулировать так:

у подобных явлений одноименные критерии подобия одинаковы, а индикаторы подобия равны единице.

Например, . (4.30)

Комплексы типа (4.22) называются критериями подобия; их принято обозначать первыми буквами фамилий ученых, работавших в соответствующей области науки. Критерии, не имеющие таких общепринятых названий, обозначаются буквой k. Все критерии подобия являются безразмерными величинами. Наличие различных связей между переменными вносит дополнительные возможности при выводе критериев подобия.

К

роме того, если для одного и того же явления определено из описывающих его уравнений несколько критериев подобия, то и различные их комбинации могут рассматриваться как критерии подобия. Например:

(4.31)

Вторая теорема утверждает, что операция интегрирования не изменяет вида критериев подобия. Ее можно сформулировать так:

критерии подобия, полученные из дифференциальных уравнений, одновременно являются критериями подобия, полученными из решения этих уравнений.

Третья теорема устанавливает признаки подобных явлений. Ее содержание: явления подобны, если условия однозначности их пропорциональны (выполняются все условия подобия), а критерии, полученные из условия однозначности, численно одинаковы.

Критерии, составленные только из величин, входящих в условия однозначности, называются определяющими. Критерии, включающие величины, не входящие в условие однозначности (они получаются в результате решения задачи), называются неопределяющими.

Согласно третьей теореме, равенство одноименных определяющих критериев вполне достаточно для того, чтобы явления были подобны. Подобные же явления характеризуются равенством всех критериев подобия. Следовательно, равенство определяющих критериев означает и равенство всех неопределяющих критериев. В соответствии с этим, каждый из неопределяющих критериев можно представить в виде функции совокупности определяющих критериев (К₁, К₂, …, К_n)

(4.32)

Уравнения, выражающие зависимость неопределяющих критериев от определяющих, называются критериальными уравнениями.