Основные свойства средней арифметической

1. Произведение средней на сумму частот равно сумме произведений вариант на частоты:

2. Если от каждой варианты отнять или прибавить какое-либо произвольное число А, то средняя уменьшится (увеличится) на это же число:

3. Если каждую варианту разделить на одно и то же число А, то средняя арифметическая уменьшится во столько же раз:

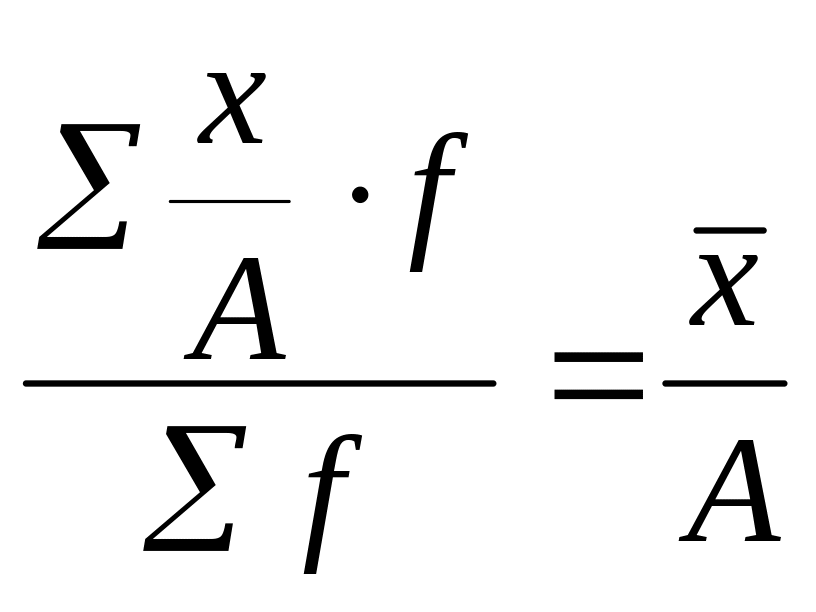или .

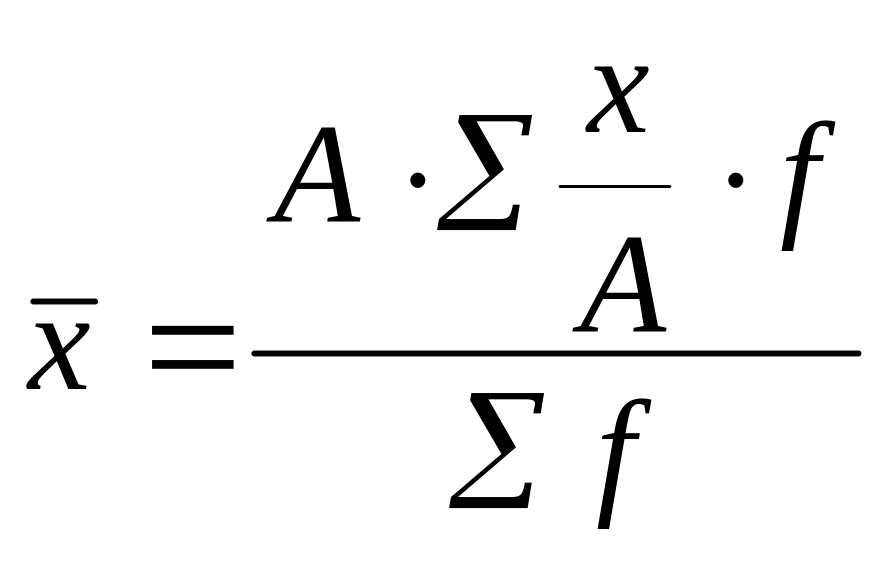4. Если каждую варианту умножить на какое-либо произвольное число А, то средняя арифметическая увеличится во столько же раз:

или .

5. Если все частоты (веса) разделить или умножить на какое-либо число А, то средняя арифметическая от этого не изменится:

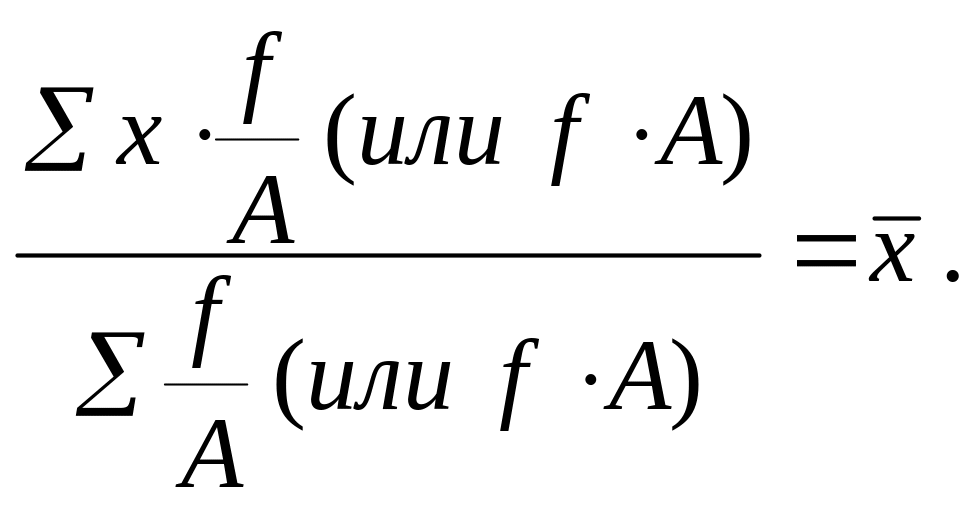
6. Сумма отклонений вариант от средней арифметической всегда равна 0:

Средняя гармоническая

Средняя гармоническая – это величина, обратная средней арифметической, т.е. состоит из обратных значений признака.

Пример 5. Расчет среднего процента выполнения плана. Имеются следующие данные:

Предпри- ятия	План	Фактич. выполне-ние плана	Степень выполне-ния плана
А	100	105	1,05 или 105 %
В	200	180	0,9 или 90 %
С	300	330	1,1 или 110 %
Итого	600	615	1,025 или 102,5 %

В примере в качестве варьирующего признака выступают показатели степени выполнения плана (варианты), а план принимает за веса (частоты). При этом средняя получается как средняя арифметическая взвешенная:

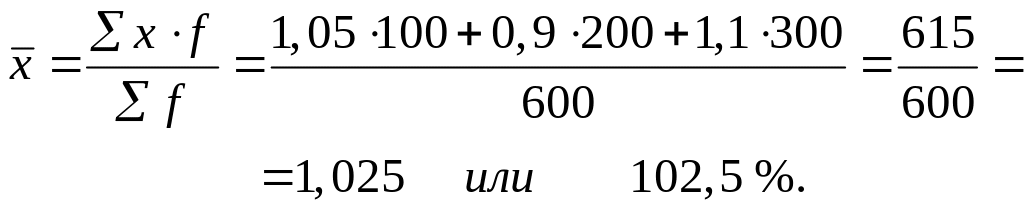
Если при определении средней степени выполнения плана за веса принимать не задание, а фактическое его выполнение, то средняя арифметическая в этом случае даст неправильный результат:

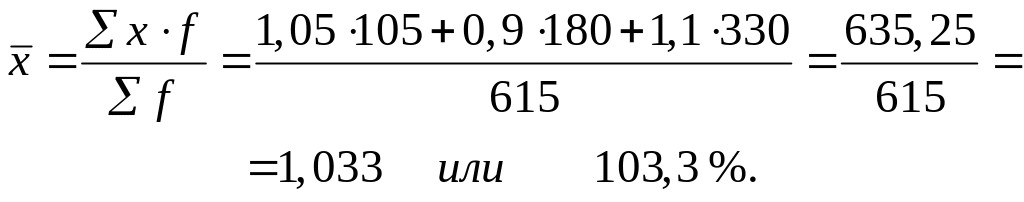
Правильный результат при взвешивании по фактическому выполнению задания даст средняя гармоническая взвешенная:

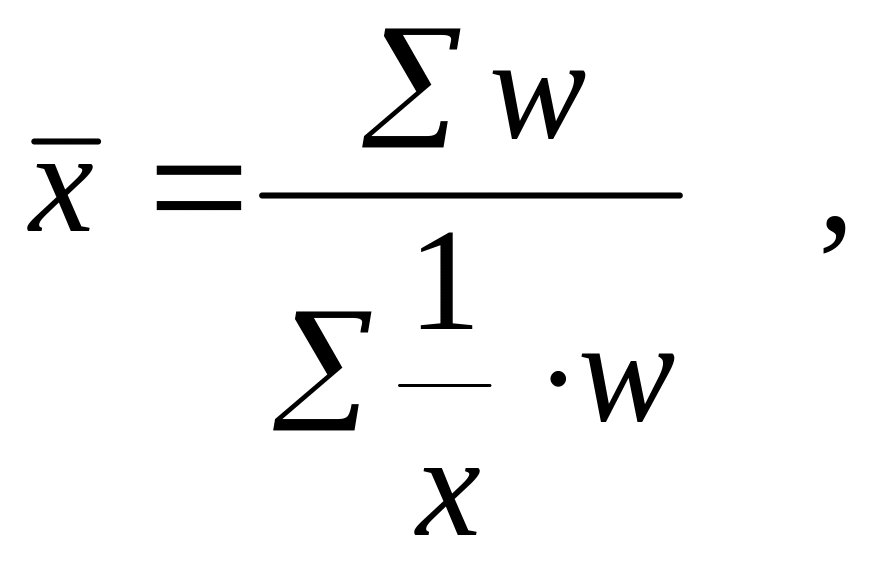
где w - веса средней гармонической взвешенной.

Тогда:

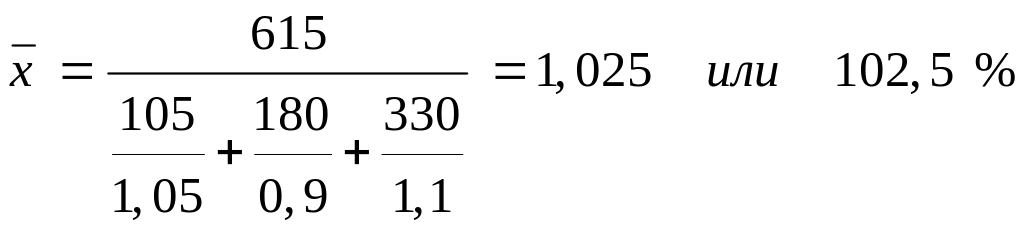
Условия применения средней гармонической

1. Среднюю гармоническую используют, когда в качестве весов применяются не единицы совокупности (носители признака), а произведения этих единиц на значения признака, т.е. .

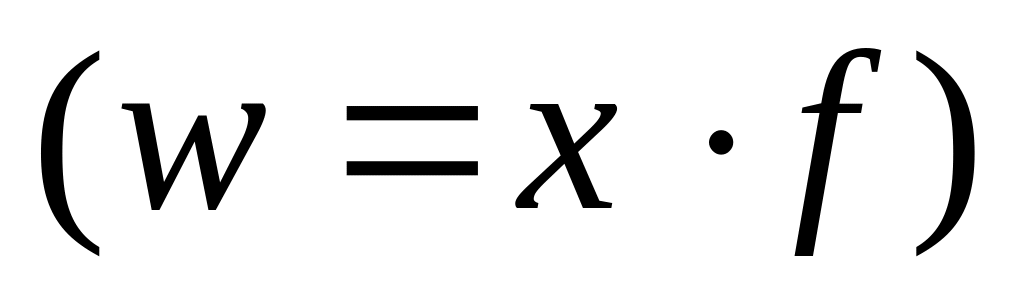Из этого правила следует, что средняя гармоническая в статистике по существу есть преобразованная средняя арифметическая, которая применяется когда неизвестна численность совокупности и приходится взвешивать варианты по объемам признака.

2. Если в качестве весов выступают абсолютные величины, всякое промежуточное действие при расчете средней должно давать экономически значимые результаты.

Например, при расчете среднего процента выполнения плана показатель выполнения плана умножаем на плановое задание и получаем фактическое выполнение плана. Если же показатель выполнения плана умножить на фактическое его выполнение, то с экономической точки зрения результат получится абсурдный. Значит, форма средней применена неверно).

3. Структурные средние

Мода и медиана – вспомогательные описательные характеристики распределения варьирующего признака, которые называются структурными средними.

Модой в статистике называется величина признака (варианта), которая чаще всего встречается в данной совокупности, т.е. это варианта, имеющая наибольшую частоту.

Моду используют только в совокупностях большой численности.

Медианой в статистике называется варианта, которая находится в середине вариационного ряда.

Медиана показывает количественную границу значения варьирующего признака, которую достигла половина членов совокупности.

1. Мода в вариационном дискретном ряду.

Пример 6. Распределение семей по числу детей.

I случай		II случай		III случай
Группы семей по числу детей	Число семей	Группы семей по числу детей	Число семей	Группы семей по числу детей	Число семей
х	f	х	f	х	f
0 1 2 3 4 5 6	10 30 75 45 20 15 6	0 1 2 3 4 5 6	5 10 15 10 15 15 15	0 1 2 3 4 5 6	10 30 75 75 20 15 6

I случай – Мода = 2

II случай - Моды нет (варианты 2, 4, 5, 6 встречаются одинаково часто).

III случай - Моды две . Две варианты имеют одинаковые частоты. В этом случае распределение называется бимодальным. Бимодальное распределение указывает на качественную неоднородность совокупности по исследуемому признаку.

2.Медиана в дискретном вариационном ряду

Чтобы найти медиану в дискретном вариационном ряду, нужно сумму частот разделить пополам и полученному результату добавить . Таким образом, мы находим медианную частоту, т.е.:

101-ая частота, варианта которой делит упорядоченный ряд пополам.

Чтобы найти значение варианты, соответствующей 101-ой частоте, нужно накапливать частоты от наименьших вариант, т.е. найти кумулятивные частоты.

Пример 6. Распределение семей по числу детей

(I случай)

Группы семей по числу детей	Число семей	Кумулятивная частота
х	F	S
0 1 2 3 4 5 6	10 30 75 45 20 15 6	10 10+30=40 40+75=115 115+45=160 160+20=180 180+15=195 195+6=201
Итого	201

Наиболее подходит кумулятивная частота , т.к. она должна быть равна или больше 101. Данная частота соответствует третьему значению варьирующего признака. Медианой будет семья, имеющая 2-их детей.

3.Мода в интервальном вариационном ряду

В интервальном вариационном ряду для нахождения приближенного значения моды в пределах определенного интервала прибегают к расчетам.

Пример 7. Распределение рабочих по заработной плате:

Группы рабочих по за- работной плате, руб.	Число рабочих
Х	f
70-80	40
80-90	50
90-100	60
100-110	145
110-120	110
120-130	80
130-140	15
Итого	500

Чтобы найти моду, необходимо определить модальный интервал данного ряда. Наибольшая частота , что соответствует модальному интервалу от 100 до 110.

Для расчета модальной величины признака, заключенного в этом интервале, применяют формулу:

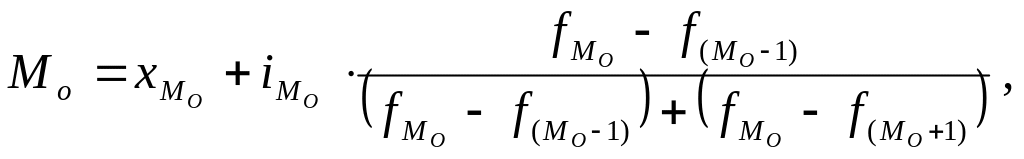
где - минимальная граница модального интервала (100);

- величина модального интервала (10);

- частота интервала, предшествующего модальному (60);

- частота модального интервала (145);

- частота интервала, следующего за модальным (110).

Для примера:

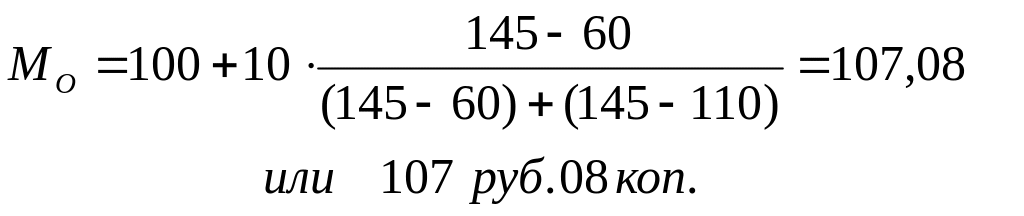
Таким образом, большая часть рабочих имеет данную заработную плату 107 руб. 08 коп.