2.5. Распределение носителей в зонах проводимости

Разрешенные зоны содержат огромное количество уровней (10²²-10²³ в 1 см³), на каждом из которых могут находиться электроны. Фактическое же количество электронов зависит от концентрации доноров и от температуры. Чтобы оценить фак­тическую концентрацию носителей в полупроводнике, нужно знать распределение уровней и вероятность заполнения этих уровней.

Энергетическое распределение электронов в твердом теле определяется статистикой Ферми-Дирака. Принципиальный ре­зультат функции распределения Ферми-Дирака дает вероят­ность того, что электрон занимает уровень, соответствующий по­тенциалу φ:

F_n(φ) = 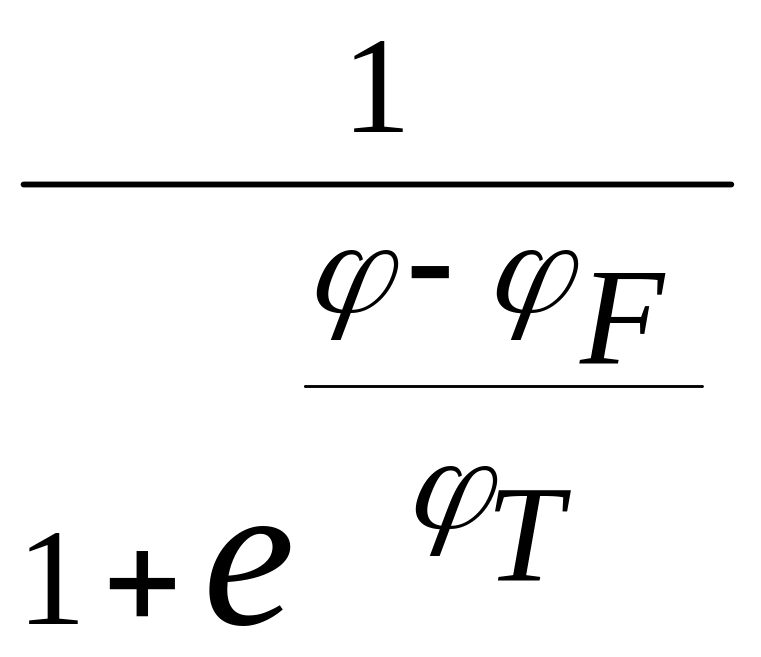, (2.2)

где φ_T = кТ — температурный потенциал, T — абсолютная тем­пература, к — постоянная Больцмана, φ_F — уровень Ферми.

Можно определить уровень Ферми как потенциал, вероят­ность заполнения которого электроном равна в точности одной второй. Функции распределения Ферми-Дирака симметричны относительно уровня Ферми. Если энергетические состояния в зоне проводимости и валентной зоне одинаковы, то уровень Фер­ми находится посередине запрещенной зоны. Это случай собст­венного полупроводника (рис. 2.11, а). В полупроводнике n-типа концентрации электронов в зоне проводимости больше, чем в случае собственного полупроводника (рис. 2.11, б), а в полупро­воднике р-типа — меньше (см. рис. 2.11, в).

Для потенциалов в несколько единиц кТ выше или ниже уровня Ферми, когда экспонента значительно больше единицы, распределение Дирака-Ферми можно заменить распределением Максвелла-Больцмана. При этом вероятность заполнения уров­ня в зоне проводимости определяется как

F_n(φ) =e^- . (2.3)

Вероятность незаполнения уровня в валентной зоне (т.е. на­личия дырки на этом уровне) определяется аналогичной функ­цией

F_p(φ) = e^- . (2.4)

Обозначим через Р(φ) плотность уровней в зоне проводимости вблизи уровня φ. Тогда Р(φ)dφ будет количеством уровней в диа­пазоне dφ. Умножив это количество на вероятность заполнения этих уровней F_n(φ), получим концентрацию свободных электро­нов с энергиями от φ до φ + dφ. Полную концентрацию свобод­ных электронов п получим путем интегрирования по всей шири­не зоны проводимости. Если принять зависимость Р(φ) ~ , то

n =N_ce^- . (2.5)

Здесь N_c — так называемая эффективная плотность уров­ней (состояний) в зоне проводимости:

N_c =0,5∙10¹⁶(m_n/ m)^3/2 T ^3/2 , где m_n – эффективная масса электрона.

Аналогичным методом получается выражение для концент­рации дырок:

p = N_v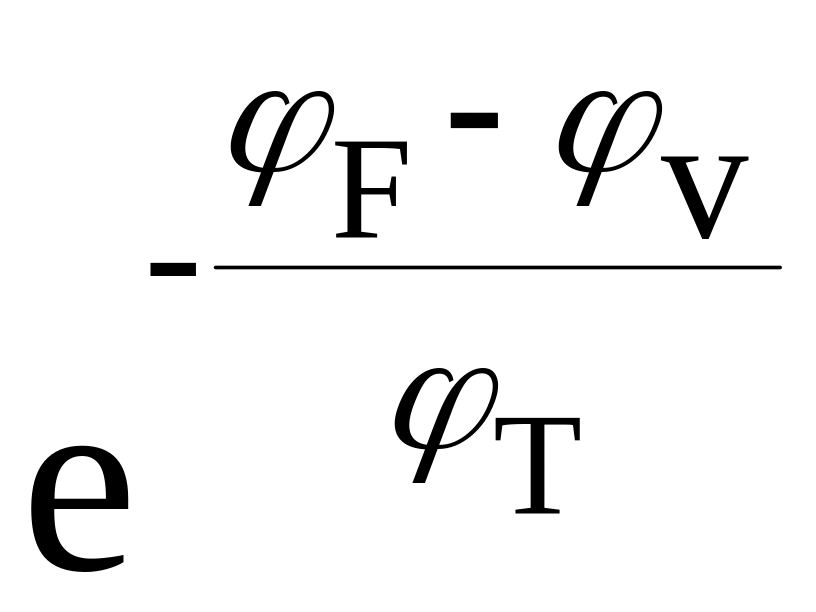 . (2.6)

Здесь N_v — эффективная плотность уровней (состояний) в валентной зоне:

N_v = 0,5∙10¹⁶(m_p/m)^3/2T^3/2, (2.7)

где m_p — эффективная масса дырки. Для кремния отношение N_c/N_v= 2,8. Часто для простоты полагают N_c = N_w.

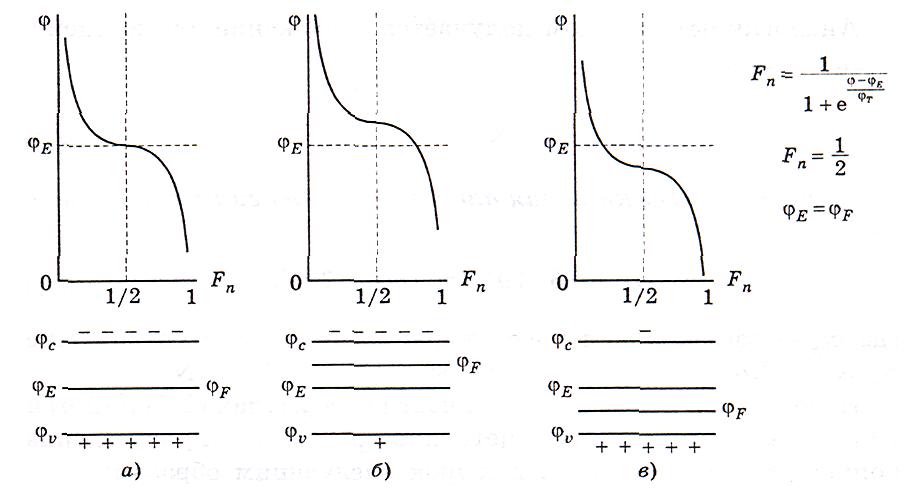
Рис.2.8. Функция распределения Ферми-Дирака для собственного, n и р- типов полупроводников: а – собственный полупроводник; б – полупроводник n-типа ; в – полупроводник р-типа.

Перемножая левые и правые части в формулах (2.5) и (2.6) и учитывая, что φ₃ = φ_c – φ_v, нетрудно представить произведение концентраций электронов и дырок следующим образом:

np = N_cN_v . (2.8)

Как видим, при неизменной температуре произведение кон­центраций— величина постоянная, т.е. увеличение одной из концентраций сопровождается уменьшением другой.

В собственном полупроводнике концентрации электронов и дырок одинаковы. Обе они обозначаются через n_i и называются собственными концентрациями. Подставляя n=n_i и p=n_i в (2.8) и извлекая квадратный корень, получаем выражение для собственной концентрации:

n_i = (2.9)

Отметим полную зависимость собственной концентрации от ширины запрещенной зоны и температуры.

Соотношение (2.8) часто записывают в более компактной форме через собственную концентрацию:

np = n (2.10)

Используя выражения (2.5) и (2.6), полагая для простоты N_c = N_v и учитывая, что φ_Е=1/2 (φ_с+φ_v), нетрудно представить отношение концентраций электронов и дырок в виде:

n/p = e . (2.11)

Подставим в левую часть (2.11) значение p =n /n из (2.10) и прологарифмируем обе части; тогда уровень Ферми запишется через концентрацию свободных электронов следующим обра­зом:

φ_F = φ_E + φ_Tln(n/n_i). (2.12 a)

Если подставить в (2.11) значение n=n /p из (2.10), то уро­вень Ферми запишется через концентрацию дырок:

φ_F = φ_E - φ_Tln(p/n_i). (2.12 б)

Вторые члены в правых частях (2.12), характеризующие концентрации носителей, называются химическим потенциа­лом. Следовательно, уровень Ферми является суммой электри­ческого и химического потенциалов. Отсюда еще одно его на­звание — электрохимический потенциал.

Одно из фундаментальных положений в физике полупровод­ников формулируется следующим образом: уровень Ферми оди­наков во всех частях равновесной системы, какой бы разнород­ной она ни была. Это положение можно записать в виде двух равносильных выражений:

φ_F=const, grad(φ_F)=0 (2.12в)

Из условия (2.12в) в одномерном случае следует, что если концентрация электронов изменяется вдоль координаты х, то возникает электрическое поле

E = φ_T

Таким образом, в неоднородно-легированных полупроводни­ках смещение подвижных носителей, обусловленное градиен­том концентрации, уравновешивается внутренним электриче­ским полем. Иногда его называют встроенным, а возникающее при этом равновесие называют больцмановским.