6.3. Ранговая корреляция и сопряжённость

a. Коэффициенты ранговой корреляции Кендалла и Спирмена

Применяется для выявления взаимосвязи между количественными или качественными показателями/признаками, если их можно ранжировать. Значения показателя X выставляют в порядке возрастания и присваивают им ранги 1, 2, . . ., n. Ранжируют значения показателя Y, предварительно расположив их попарно с сопряжёнными значениями показателя Х, т. е. получают соответствующий первому ряд k₁, k₂, . . ., k_n . Коэффициент корреляции Кендалла рассчитывают по формуле:

, (6.39)

где S = P − Q; P – суммарное число наблюдений, следующих за текущими наблюдениями с большим значением рангов Y; Q — суммарное число наблюдений, следующих за текущими наблюдениями с меньшим значением рангов Y (равные ранги не учитываются!). Величину S можно рассчитать также по соотношению

S = = 2N – n(n – 1)/2; sign(a – b) = (6.40)

где N – количество тех пар замеров показателей (признаков), для которых при j > i и k_j > k_i. Очевидно   [– 1; 1].

Если исследуемые данные повторяются (имеют одинаковые ранги), то в расчетах используется скорректированный коэффициент корреляции Кенделла:

, (6.41)

где t – число связанных рангов в ряду X и Y соответственно.

Первый коэффициент корреляции был предложен Спирменом (1904 г.) и носит его имя:

. (6.42)

Коэффициент Спирмена также определён как и обычный выборочный коэффициент корреляции на отрезке [–1, 1].

В общем виде распределение коэффициента ранговой корреляции Спирмена достаточно сложно для его использования; отсутствуют и соответствующие таблицы для вычисления соответствующих вероятностей. Однако, если совместное распределение признаков является нормальным, то при n » 10 выборочный коэффициент корреляции r связан с коэффициентом Сптрмена r_s соотношением

r ≈ 2 sin(πr_s /6).

Коэффициенты Спирмена и Кендалла можно использовать в качестве критереев для проверки гипотезы H₀ о независимости признаков. При справедливости нулевой гипотезы статистики (6.39) и (6.42) имеют симметричные распределения, первые моменты которых имеют вид:

(6.43)

Более того, если объём выборки достаточно велик (практически, если n  10), распределения обоих выборочных ранговых коэффициентов можно аппроксимировать нормальным распределением с параметрами, задаваемыми (6.43), что позволяет находить верхние и нижние критические значения выборочных коэффициентов ранговой корреляции с заданным двусторонним уровнем значимости  . При этом надёжность принятия нулевой гипотезы увеличивается, так как действительный уровень значимости несколько меньше величины, получаемой на основе нормального приближения. Так для коэффициенты Спирмена, согласно нормальному приближению

, а верхнее критическое значение определяется из уравнения

с помощью таблиц процентных точек нормального распределения (табл. VI Приложения). Нулевая гипотеза отвергается по обоим критериям при больших значениях статистик критериев, т.е. при условии

. (6.44)

Оба критерия, в условиях выполнимости гипотезы независимости, являются асимптотически эквивалентными, но коэффициент ранговой корреляции Спирмена предпочтительней, так как при существенно большей простоте вычисления выборочной статистики имеет большую мощность при приблизительно одинаковом уровне значимости.

Однако наиболее удобно применение коэффициента ранговой корреляции Кендалла при определении степени статистической связи между так называемыми категоризированными переменными.

Ранги могут быть получены и для числовых наблюдений, но можно представить себе случайные величины, для которых числовые данные получить трудно или даже невозможно. Таковы: любые классификации каких либо объектов по тому или иному признаку, например, людей по росту, по цвету волос и т. п.; дихотомические переменные, каждая из которых либо присутствует, либо отсутствует на данном объекте.

Замечание 6.6. Категоризированная «переменная» может просто представлять собой подходящую классификацию числовой переменной по группам, а может вообще не выражаться в терминах какой-либо исходной числовой переменной, причём в этом случае категоризация может быть как упорядоченной (т.е. изменение переменной можно как то упорядочить) так и неупорядоченной.

Следует иметь в виду, что иногда две и более изучаемые переменные могут быть одной и той же переменной, наблюдаемой в различных ситуациях (например, до и после некоторого события) или в двух связанных между собою выборках. В таких случаях говорят об однородных категоризациях.

Очевидно, однородные категоризации могут применятся и в случае числовых переменных, быть как упорядоченными так и не упорядоченными.

Во всех этих случаях в качестве обрабатываемых данных имеем таблицу m  k в виде:

i j	1 2 . . . m	nj·
1 2 . . . k	n11 n12 . . . n1m n21 n22 . . . n2m . . . . . . . . . . . . nk1 nk2 . . . nk m	n1· n2· . . . nk·
n i	n·1 n·2 . . . n·m	n

Табл. 6.1

Здесь n_ji , таким образом, либо наблюдённая частота соответствующей числовой переменной, либо подходящая классификация степени выраженности некоторого качественного признака в разных ситуациях или на разных объектах, а как крайность – 0 или 1, если этот показатель дихотомический. То есть, в случае двух дихотомических признаков будет таблица 2  2.

b. Коэффициенты сопряжённости.

Таблицы типа таблицы 6.1 обычно называют таблицами сопряжённости. Поэтому и коэффициенты статистической связи между такими переменными часто также называют коэффициентами сопряжённости. Они удобны при исследовании статистических связей между признаками, не поддающимися количественному описанию, а особенно при исследовании нескольких признаков/переменных разной природы. В этом случае величины n_ji представляют k ранжировок соответствующих признаков на m объектах (или по m измерениям). Первая строка такой таблицы – набор чисел 1, 2, . . ., m.

В качестве единой выборочной меры статистической связи в этом случае Кендалл и Бэбингтон Смит предложили использовать коэффициент согласованности W, называемый также коэффициентом конкордации:

. (6.45)

Коэффициент W принимает значения на отрезке [0, 1] и обычно используется для проверки нулевой гипотезы H₀ о совместной независимости k признаков. Признаки являются независимыми, если для любого наугад выбранного столбца матрицы, представленной таблицей 6.1, ранги r_1i , r_2i , . . . , r_ki являются взаимно независимыми случайными величинами. В предположении выполнимости нулевой гипотезы статистика W имеет распределение с математическим ожиданием и дисперсией, определяемых соотношениями

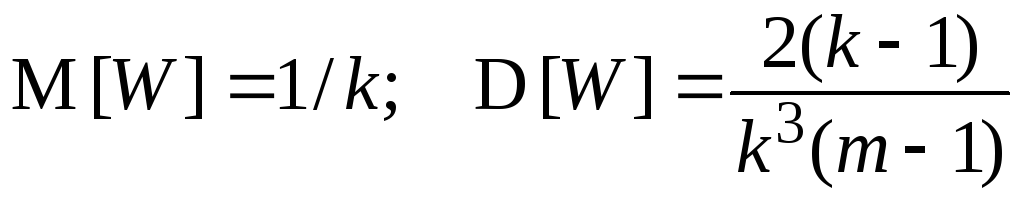. (6.46)

Применение статистики W аналогично применению статистик Спирмена и Кендалла. Таблицы точного распределения коэффициента согласованности применительно к нулевой гипотезе, необходимые для определения критических значений статистики W, можно найти в табл. Большева и Смирнова. Однако, для прикладных задач уже при числе наблюдений (объектов) m  5 можно использовать распределение хи-квадрат, так как статистика

Ŵ = k (m – 1) W (6.47)

распределена по закону хи-квадрат с ν = (m – 1) степенями свободы. С помощью этой таблицы определяют верхнее критическое значение ŵ_,ν для проверки нулевой гипотезы о независимости признаков с односторонним уровнем значимости  . При этом приближённое решение обеспечивает большую надёжность в отношении справедливости нулевой гипотезы.

Рассмотрим задачу статистической связи между двумя величинами (признаками), когда категоризация проведена на основании наличия или отсутствия этих признаков x, y. Тогда табл.6.1 переходит в таблицу 2х2 вида:

	y	не y
x	a	b	a + b
не x	c	d	c + d
	a + c	b + d	n = a + b + c + d

Табл. 6.2

Если между x и y не существует никакой связи, то есть, если обладание признаком x не связано с обладанием признаком y, то доля объектов с признаком x среди объектов с признаком y должна быть равна доле объектов с признаком x среди объектов, не обладающих признаком y, а также доле среди всех объектов. Таким образом, признаки полагаются несвя-

занными по данной совокупности из n наблюдений, если

. (6.48,a)

Аналогично получаются следующие соотношения:

. (6.48,b)

Из (6.48,a и b) можно получить ожидаемые, в предположении независимости x и y, частоты:

. (6.49)

Если теперь для какой-либо таблицы a > a^*, что означает, что доля x среди y больше чем среди не-y, то x и y называются положительно сопряжёнными, или просто сопряжёнными. Если a < a^*, то говорят об отрицатедьнй сопряжённости.

Для проверки гипотезы H₀ об отсутствии сопряжённости между признаками x и y можно использовать статистику критерия хи-квадрат Пирсона:

, (6.50)

где –наблюдаемые частоты,ω – ожидаемые частоты в предположении отсутствия сопряжённости. Суммирование ведётся по всем клеткам таблицы. Для таблицы 2 х 2 получаем:

(6.51.a)

Статистику (6.51.a) применяют обычно с учётом так называемой поправки на непрерывность, предложенную Йетсом в 1934 г. В этом случае она имеет вид

. (6.51.b)

При практическом применении критериев, основанных на этих статистиках, наиболее надёжные результаты достигаются лишь при достаточно больших выборках: в общем случае при n  40 и при n  20, если ни одна из ожидаемых частот не меньше 5. В самом общем случае можно применить точный критерий, впервые предложенный Фишером

. (6.52)

Величина даёт вероятность осуществления рассматриваемой таблицы. Эту вероятность следует просуммировать с величинами , полученными для таблиц таких же или ещё более неправдоподобных. Эти таблицы получаются из исходной заменой частот в клетках, но с сохранением величин сумм по строкам и столбцам. Полученную таким образом некоторую величину так называемой полной вероятности P, сравнивают затем с заданным уровнем значимости . При P   нулевая гипотеза об отсутствии сопряжённости отвергается.

Для вычисления меры сопряжённости признаков применяются гак называемые коэффициенты сопряжённости. Все они изменяются в интервалах

(–1, 1) или (0, 1) и случай отсутствия сопряжённости соответствует нулевому значению коэффициентов. Это позволяет согласовать свойства таких коэффициентов со свойствами обычного коэффициента корреляции.

Рассмотрим некоторые из таких коэффициентов.

Коэффициент Юла

(6.53)

Величина D однозначно определяет отклонение от независимости. Естественное требование возрастания коэффициента сопряжённости с возрастанием D, что в данном случае выполняется. Кроме того, коэффициент Q = 0, когда признаки независимы, т.е. если D = 0; принимает значение + 1 только тогда, когда bc = 0, т.е. в случае полной положительной связанности, а значение –1

— когда ad = 0, т.е. в случае полной отрицательной сопряжённости.

Замечание 6.7. Под полной связью понимается здесь такая связь, когда либо все x одновременно являются y, либо наоборот, все y являются x. Если же все x одновременно являются y и все y являются x, то такую связь следует скорее называть абсолютной.

Юл предложил, кроме того, так называемый коэффициент коллигации

. (6.54)

Коэффициент коллигации удовлетворяет всем требованиям, предъявляемым к коэффициентам сопряжённости.

Однако легко показать, что Q = 2Y/(1 + Y²), поэтому почти никакого выигрыша использование коэффициента Y по сравнению с коэффициентом Q не даёт. Единственное преимущество коэффициента коллигации в том, что его модуль полностью совпадает с коэффициентом, характеризующим относительное уменьшение вероятности ошибки, вызванное знанием одной категории при предсказании другой (т.е. Y имеет вероятностный смысл):

|Y|   =

Коэффициент Форбесса.

. (6.55)

Коэффициент F представляет собой отношение числа объектов с обоими признаками к математическому ожиданию этой величины, в предположении независимости признаков. Очевидно, 0  F  1. Этот коэффициент имеет один существенный недостаток: его величина зависит от встречаемости признаков на объектах. Точнее: F возрастает с уменьшением встречаемости.

Редуцированный коэффициент корреляции.

Этот коэффициент сопряжённости непосредственно связан со статистикой ², определяемой соотношениями (6.51.a,b).

. (6.55)

Очевидно, что он равен нулю, когда D = 0 и возрастает с возрастанием D. Если V² = 1, то (a + b)(a + c)(b + d)(c + d) = (ad – bc)² или 4abcd + a ²(bc + bd + cd) + b ²(ac + ad + cd) + c ²(ab + bd + ad) + d ²(ab + ac + bc) = 0.

Так как ни одна из частот не может быть отрицательной, то это уравнение имеет решение только в случае, когда по крайней мере два из чисел a, b, c, d равны нулю. Случай, когда равны нулю частоты одной строки или однргр столбца, является вырожденным, потому имеет смысл рассматривать льшь два варианта: a = d = 0 – при этом V = – 1; b = c = 0 – при этом V = + 1, т.е. эти варианты задают абсолютную отрицательную и положительную связь в том смысле, как о ней говорилось ранее.

Тетрахорический и бисериальный коэффициенты корреляции.

Всё рассмотренные критерии и коэффициенты позволяют вполне успешно решать задачу проверки наличия и измерения степени взаимозависимости между двумя категоризированными переменными, причём задачу непараметрическую (т.е свободную от вида и параметров распределений изучаемых признаков). Для полноты картины рассмотрим также важный случай параметрической задачи такого вида.

Рассмотрим оценивание коэффициента корреляции в двухмерной нормальной совокупности, когда выборочные данные известны не во всех подробностях, т.е. могут быть представлены также в виде таблицы типа табл. 6.2.

Если эта таблица получена с помощью двойной дихотомии двумерного нормального распределения, то можно найти такие h и k, что

.

Подогнав таким способом одномерные нормальные распределения к маргинальным частотам таблицы, оценку r_t коэффициента корреляции  по выборке объёма n можно определять как решение уравнения

, (6.56)

где при этом

–полиномы Чебышева – Эрмита; (x) =

= (2π) ^{– 1/2}exp(– x ²/2); – так называемая тетрахорическая функция, введённая и табулированная К. Пирсоном как раз для рассматриваемой задачи.

Получаемая оценка коэффициента корреляции r_t также называется тетрахорическим коэффициентом корреляции. Для тетрахорического коэффициента в точной форме неизвестны выборочное распределение и даже его стандартная ошибка. Впрочем, известно асимптотическое выражение его стандартной ошибки, найденное Пирсоном. Рассматриваемый коэффициент наиболее часто используется психологами и биологами. Вычисление его в общем случае – достаточно сложная задача, так как требуется либо громоздкое решение уравнения (6.56) методом последовательных приближений, либо интерполяция (обычно, линейная) по таблицам, содержащим значение интеграла d/n в зависимости от  при различных значениях h и k. Существуют более простые способы вычислений, основанные на номограммах и таблицах для стандартной ошибки в приближённой форме. Однако неизвестно, при каких объёмах выборок можно с требуемой надёжностью пользоваться такими стандартными ошибками.

Замечание 6.8. В биологической литературе в качестве тетрахорического коэффициента корреляции нередко используют коэффициет

T₄ = (|ad – bc| – 0,5n)/[(a + b)(c + d)(a + c)(b + d)]^1/2,

являющийся частным случаем (для таблицы 2х2) рассматриваемого далее коэффициента Чупрова.

В этом варианте значимость полученного коэффициента можно оценить (в предположении некоррелированности или несопряжённости двух нормально распределённых дихотомических признаков) по критерию хи-квадрат: ² = nT₄², с числом степеней свободы ν = 1. Нулевая гипотеза об отсутствии сопряжённости отвергается при превышении критического значения при выбранном уровне значимости.

Рассмотрим теперь задачу о корреляции двух переменных, одна из которых является дихотомией (характеризуется как «да» – «нет» или как-то иначе разбит на 2 альтернативных класса), а вторая представлена в числовом либо категоризированном виде. Имеем таблицу 2 х q.

Если, по-прежнему верно предположение о двухмерном нормальном распределении генеральной совокупности, то хорошей оценкой коэффициента корреляции является т.н. бисериальный коэффициент корреляции

, (6.57)

где индекс j нумерует y-сечения дихотомической переменной x; n_j – число наблюдений в этом сечении; n =  n_j ; m_j и s_j - оценки среднего и среднеквадратичного отклонения в j – том сечении; m_y и s_y – оценки среднего и среднеквадратичного отклонения величины y.

Хотя в данном случае может быть применён и обычный коэффициент корреляции в форме (6.4.b), но в виде (6.57) его можно использовать для любых выборок объёма n < 100.

Выборочное распределение полученной оценки, как и в случае тетрахорического коэффициента корреляции, неизвестно. Имеется, найденное К. Пирсоном, асимптотическое выражение для выборочной дисперсии этого коэффициента, но неясно как велико должно быть n, чтобы использование этой статистики давало надёжные результаты.

Замечание 6.9. Приведённые данные не позволяют ожидать, что тетрахорический и бисериальный коэффициенты корреляции могут быть очень эффективными оценками для коэффициента корреляции, так как :

— во-первых, они используют слишком мало информации о переменных;

— во-вторых, решающим для обоих методов является предположение о двумерной нормальности исходного распределения (а иначе неясно, что оценивают эти коэффициенты).

Рассмотрим теперь более общую ситуацию, когда обе переменные классифицированы на более чем две категории. Тогда данные представлены в виде таблицы 6.1 размером m x k..

Если бы две исследуемые переменные были независимы, то частота в клетке таблицы на пересечении строки i и столбца j была бы равна

. (6.58)

Отклонение от независимости в данном случае, по аналогии с (6.53), измеряется величиной .

Проверку гипотезы H₀ независимости двух исследуемых переменных можно провести на основе критерия хи-квадрат, который на случай таких таблиц обобщается следующим образом

. (6.59)

Предлагаемая статистика при выполнении нулевой гипотезы о независимости асимптотически имеет ² – распределение с ν = (m – 1)(k – 1) степенями свободы. Рассматриваемые ниже меры связи для таблиц m x k. основаны на непосредственном использовании статистики (6.59).

Коэффициент сопряжённости Пирсона.

Предлагаемый коэффициент представляет собой непосредственное отображение статистики (6.59) на отрезок [0, 1]:

. (6.60)

При конечных m и k (что и имеет место на практике) коэффициент P имеет недостатки. Очевидно, что 0 ≤ P ≤ 1. Он обращается в ноль, как это и должно быть, при полной независимости, и наоборот, если P = 0, то χ² = 0, так что каждое отклонение D_{i j} = 0, что означает отсутствие сопряжённости. Однако, коэффициент P не имеет одного и того же верхнего предела для всех случаев. Рассмотрим случай m = k , причём отличны от нуля только элементы главной диагонали. Тогда n_{i ∙}= n _∙j = n_{i i} для всех i , и поэтому, согласно (6.59) χ ² = n(m – 1), и в соответствии с (6.60) P = {1 – 1/m}^1/2.

Таким образом, даже в случае полной связи признаков значение P (достигающее в этом случае максимума) зависит от числа строк в таблице сопряжённости.

Коэффициент сопряжённости Чупрова.

Коэффициент рассчитывается по формуле

. (6.61)

Коэффициент T  [0, 1] и достигает значения +1 в случае полной положительной связи при m = k , но не обладает этим свойством при m ≠ k.