3.3 Оценки параметров нормального распределения.

Пусть X = (x₁, x₂, …, x_n)  N(a,  ²).

a). Доверительный интервал для а при условии, что  ² известно.

Так как , то с помощью таблиц стандартного нормального распределения можно найти числоq > 0 такое, что Ф(–q) = α/2. Тогда Ф(q) = 1 – α/2 по свойствам функции Лапласа. Это значит, что

P{– q<<q} = Ф(q) – Ф(–q) = 1 – α,

Или, после преобразований,

. (3.4)

Тем самым построен доверительный интервал 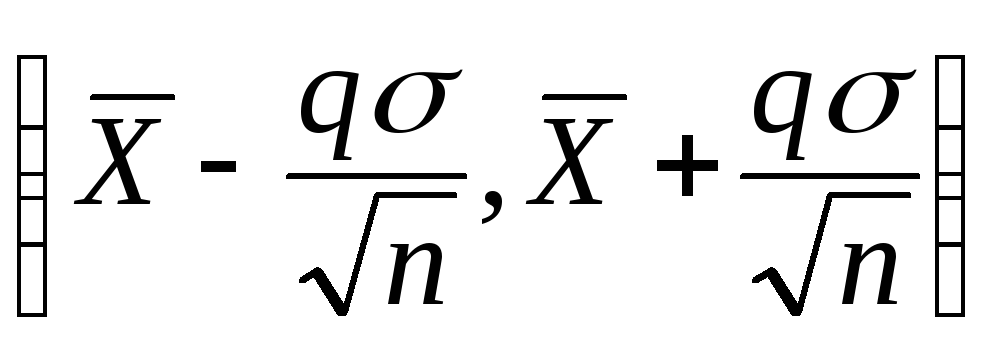длиной , то есть при большихп можно довольно точно локализовать значение неизвестного параметра а.

b). Доверительный интервал для а при условии, что  ² неизвестно.

Интервал, сконструированный в предыдущем пункте не годится, так как содержит неизвестный параметр . Но похожую конструкцию, не содержащую , содержит следствие рассмотренной выше теоремы: , т.е. имеет распределение Стьюдента сп – 1 степенью свободы. Используя таблицы этого распределения найдём число q > 0 такое, что Т_{n – 1}(–q) = α/2;

T_{n – 1} (q) = 1 – α/2. Тогда

P{– q < <q} = T_{n – 1} (q) – Т_{n – 1}(–q) = 1 – α,

и после преобразований получаем доверительный интервал

. (3.5)

с). Доверительный интервал для  ² при условии, что известно а.

Случайные величины (x_j - a)/ независимы и имеют стандартное нормальное распределение, поэтому . Из таблиц распределения

χ_n² найдём числа q₁ и q₂ такие, что χ_n²(q₁) = α/2 и χ_n²( q₂) = 1 – α/2. Тогда

P=χ_n²( q₂) – χ_n²(q₁) = 1 – α.

После несложных преобразований, получаем

P. (3.6)

d). Доверительный интервал для  ² при условии, что а неизвестно.

Воспользуемся тем, что .Из таблицраспределения находим числа q₁ и q₂ такие, что χ_n–1²(q₁) = α/2 и χ_n–1²( q₂) = 1 – α/2. Тогда

P = χ_n–1²( q₂) – χ_n–1²(q₁) = 1 – α,

и после преобразований получаем доверительный интервал

P. (3.7)

3.4 Интервальное оценивание параметров распределений, отличных от нормального

К сожалению, построить точные доверительные интервалы удаётся только для параметров нормального распределения. В общем случае, для параметров других распределений, таких хороших конструкций нет. Однако для параметров многих распределений удаётся построить асимптотические доверительные интервалы, в том числе с помощью нормального приближения.

В частности, если неизвестный параметр θ генерального распределения F(x, θ) можно выразить через один из моментов распределения: θ = g(a_k), k ≥ 1, причём функция g дифференцируема и g^′(a_k) ≠ 0. Предполагается также существование момента a_2k , так что  ² = DX^k = a_2k – a_k². Рассматривая ММ – оценку θ^*= g(a_k^*), в силу близости (при больших п) a_k и a_k^*, можно воспользоваться линейным приближением в разложении в ряд Тейлора:

θ^*= g(a_k^*) ≈ g(a_k) + (a_k – a_k^*) g^′(a_k).

Отсюда получаем

.

При больших п распределение правой части стремится, в силу ЦПТ, к стандартному нормальному. Задавая тогда доверительную вероятность 1 – α, находим по таблице стандартного нормального распределения число q > 0 такое, что Ф(– q) = α/2, Ф(q) = 1 – α/2. Тогда

Ф(q) – Ф(– q) = 1 – α.

Чтобы решить это неравенство относительно θ потребуем еще непрерывности функции h(θ) = ,чтобы для асимптотически несмещённых оценок h(θ) ≈ h(θ^*). Тогда получаем асимптотический доверительный интервал:

P. (3.8)

Пример 3.1. Требуется получить доверительный интервал для параметра λ распределения Пуассона. Здесь λ = a₁, то есть k = 1, g(y) = y. Тогда h(λ) = , и получаем для параметраλ асимптотический доверительный интервал:

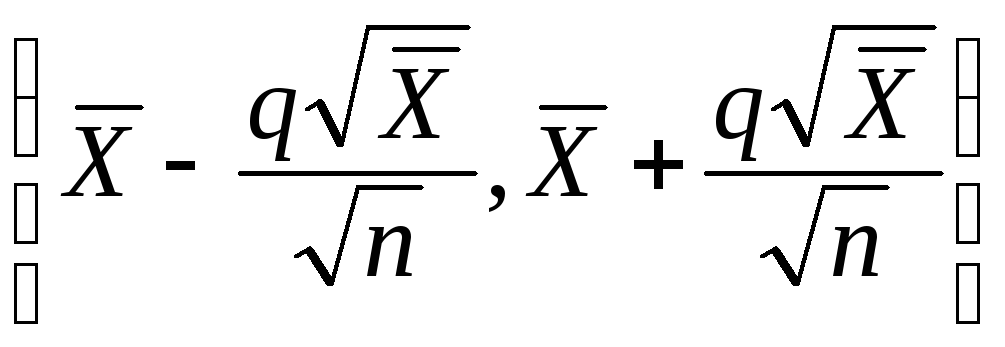, где – выборочное среднее . (3.9)

Пример 3.2. Рассмотрим схему независимых испытаний Бернулли, где n – общее число испытаний, m – число «успехов» в этой серии испытаний, p – вероятность «успеха» в отдельном испытании. Пусть n достаточно велико, а значение p не слишком близко к 0 или 1, так что можно воспользоваться асимптотикой Муавра – Лапласа.

При этом доверительный интервал для p имеет вид

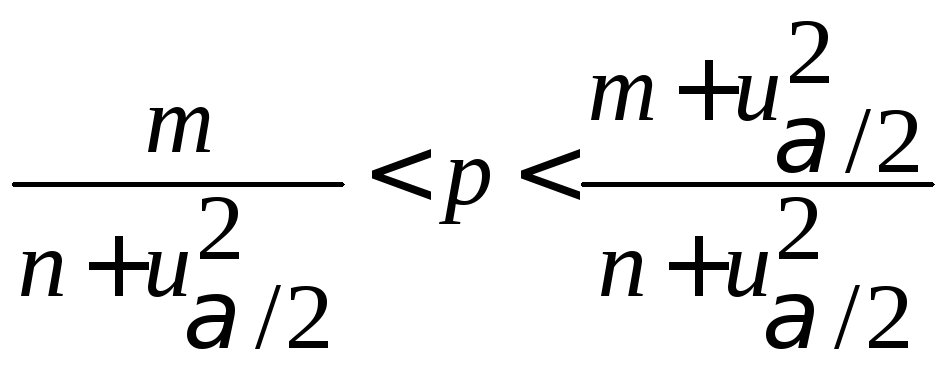(3.10)

где определяется по заданной вероятности ошибки α по таблице 6 приложения VI (в этом случае γ = α/2).

Представляют интерес крайние случаи:

приm = 0,

при m = n. (3.11)

4. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ.