Раздел I основные методы математической статистики

(ТЕОРЕТИЧЕСКИЕ ОСНОВЫ СТАТИСТИЧЕСКИХ МЕТОДОВ И

РЕКОМЕНДАЦИИ ПО ИХ ПРАКТИЧЕСКОМУ ПРИМЕНЕНИЮ)

1. Генеральная совокупность и выборка

1.1 Выборочный метод. Первичная обработка выборочных (экспериментальных) данных.

Определение 1.1. Математическая статистика – это наука, занимающаяся разработкой методов сбора, регистрации и обработки результатов наблюдений (измерения) с целью познания закономерностей случайных массовых явлений.

Результаты измерений (наблюдений) называют статистическими данными. В зависимости от поставленной задачи математической статистики могут быть сформулированы в различных формах:

• приближённое определение неизвестного закона распределения случайной величины (с. в.);

• приближённое определение неизвестных параметров распределения;

• проверка правдоподобия гипотез о распределении.

Одним из основных способов сбора статистических данных является выборочный метод. Пусть - случайная величина с функцией распределения. Если в ходе случайного эксперимента наблюдается одно значение случайной величины, то существенной информации о распределенииполучить нельзя. Однако, если производится большое количество независимых друг от друга одинаковых случайных экспериментов, в каждом из которых наблюдается значение случайной величины, то при достаточно большом количестве экспериментов можно получить оценкии её характеристик.

Определение 1.2. Вся исследуемая совокупность однородных объектов называется генеральной совокупностью.

Определение 1.3. Множество из n объектов, отобранных случайным образом из генеральной совокупности, называется выборочной совокупностью или выборкой.

Другими словами, это набор из независимых с. в., каждая из которых имеет распределение.

Определение 1.4. Случайная величина, являющаяся функцией от случайной выборки называется статистикой.

Определение 1.5. Набор упорядоченных с.в. называется вариационным рядом. При этом называется первойпорядковой статистикой, называется-той порядковой статистикой.

Определение 1.6. Метод, основанный на том, что по итогам изучения выборки, выделенной из данной генеральной совокупности, делается заключение о всей генеральной совокупности, называется выборочным методом.

Определение 1.7. Выборка называется репрезентативной, если каждый объект генеральной совокупности имеет одинаковую возможность попасть в выборку. В соответствии с законом больших чисел, результаты изучения такой выборки и выводы будут близки к результатам, какие могли быть получены, если бы исследовалась вся генеральная совокупность.

Замечание 1.1. Одна из основных задач математической статистики состоит в построении по случайным выборкам других с. в., которые служат оценками параметров или распределений. Эти оценки при неограниченном увеличении числа наблюдений компонент выборки, сходятся с вероятностью единица или по вероятности к истинному значению параметра наблюдаемой величины или ее распределению. Прикладная статистика имеет дело с конкретными реализациями с. в., полученными в ходе случайных экспериментов. Она использует оценки и формулы математической статистики, при этом вместо с. в.ξ_i подставляются их конкретные реализации.

Рассмотрим задачу о построении оценки для функции распределения с. в._ξ по случайной выборке X = (x₁, …, x_n). Такой оценкой будет служить так называемая эмпирическая функция распределения.

Определение 1.8. Эмпирической функцией распределения, построенной по случайной выборке X = (x₁, …, x_n) называется случайная функция

, (1.1)

где - индикатор множества.

Замечание 1.2. Для конкретной реализации выборки и фиксированного числавеличинаравна доле тех значенийкоторые меньше.

Замечание 1.3. Свойства эмпирической функции распределения аналогичны свойствам обычной функции распределения. Её можно описать следующим образом. Отдо первой порядковой статистикиx₍₁₎значениеравно 0. Далее значениеувеличивается нав каждой из точекx_(k), т.е.при . Прибольшем чем- тая порядковая статистикаx_(n)значениеравно единице.

Теорема 1.1. Для любого фиксированного с.в.имеет следующее распределение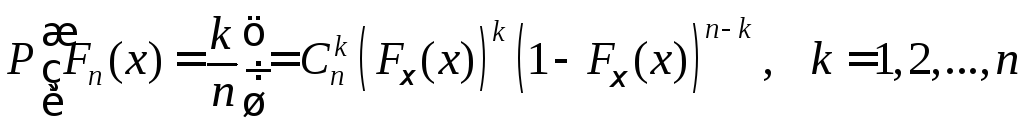

Пример 1.1. Пусть наблюдается следующая реализация выборки:

0,2; – 1,7; – 3,8; 2,1; 6,2; – 3,4; 4,1; 1,8; – 1,3; 2,8.

График эмпирической функции распределения для этой реализации имеет вид, показанный на рис. 1.1.

Это кусочно-непрерывная функция, имеющая в точках выборки скачки 0,1.

Рис. 1.1

Эмпирическая функция распределения является хорошей оценкой для функции распределения.

Определение 1.9. Эмпирической плотностью распределения, построенной по случайной выборке называется случайная функция

.

Замечание 1.4. График функциичасто называют гистограммой распределения случайной величины _ξ. Чтобы его построить нужно разбить всю вещественную ось на интервалы длиныи каждому интер-

валу поставить в соответствие число, где

, т.е. число тех Рис. 1.2

значений , которые попадают на интервал.

Пример 1.2. Пусть наблюдается следующая реализация выборки, состоя- щая из 20 компонент: 0,78; – 0,12; – 0,61; 0,92; 0,55; 1,63; – 1,16; 0,01; – 0,45; 0,20; – 0,38; 0,62; 0,46; – 0,22; 1,11; – 0,77; 0,37; 0,72; – 0,24; 0.42.

Гистограмма с шагом h = 0,4 для этой реализации имеет вид, показанный на рис. 1.2.

Замечание 1.5. При построении эмпирической плотности распределенияследует выбирать в зависимости от, так чтобы при большихи малыхпроизведениетоже было достаточно большим, например.

Определение 1.10. Квантилью порядка р функции распределения называется такое число, для которого, а, если оно единственно, а если множество таких чисел составляет целый интервал, то полагаем- средняя точка интервала.

Замечание 1.6. Для непрерывной, строго возрастающей функциипри любомквантильединственна и.

Определение 1.11. Квантиль порядка p =дляназываетсямедианой распределения.

Для случайной величины с непрерывной строго возрастающей вероятность того, что она примет значение меньше медианы, равна вероятности того, что она примет значение больше медианы, и равна 0,5.

Определение 1.12. Выборочной квантилью порядка будем называть квантиль порядкар для эмпирического распределения , т.е.

(1.2)

Определение 1.13. Выборочная медиана – это медиана для эмпирического распределения , т.е.

Пример 1.3. Вычислить выборочную квантиль порядка для реализации выборки примера 2. Определить выборочную медиану.

Т.к. , то. Следовательно,. Поскольку- чётное число, то выборочная медиана равна