3). Критерий Смирнова – Мизеса (критерий ω2)

В качестве меры расхождения эмпирической F*(x) и гипотетической F(x) функций распределения рассматривается средний квадрат отклонения по всем возможным значениям случайной величины, что влечёт потерю некоторой информации по сравнению с критерием Колмогорова. Итак, выборочная статистика имеет вид

ω² = =(4.4)

Так как эмпирическая функция распределения F*(x) или F_n (x) является несмещённой оценкой теоретического распределения, т.е. M[F*(x)] = F(x), а дисперсия D[F*(x)] = F(x)(1 – F(x)), то, при выполнении нулевой гипотезы согласия, среднее значение и дисперсия статистики ω² равны: M[ω²] = 1/6n; D[ω²] = (4n – 3) /180n³; не зависят от гипотетического распределения и в асимптотике равны нулю. Удобнее использовать статистику Z = n ω², для которой M[Z] = 1/6. По сравнению с распределением Колмогорова распределение статистики Z довольно быстро сходится к предельному распределению (уже при n ≥ 40 они практически совпадают), которое табулирована. В Приложении III в таблице 1 приведены некоторые критические значения для распределения Z. Нулевая гипотеза отвергается с уровнем доверия γ при превышении выборочной статистики критерия над критическим значением.

4.3. Проверка гипотез относительно двух выборок

а. Критерий Колмогорова – Смирнова однородности двух выборок.

Пусть X = (x₁, …, x _n)  F; Y = (y₁, …, y _m)  G, где F и G – непрерывные функции распределения.

Проверяется гипотеза

H ₀ : F = G против H₁ : F ≠ G. (4.5)

Предлагаемый критерий – асимптотический с уровнем значимости 1– ε.

Замечание 4.6. Если проверяемая гипотеза о двух выборках имеет вид (4.5), то есть проверяется гипотезао совпадении двух распределений, то критерии, привлекаемые для её решения, называюткритериями однородности. Но нередко в задаче о двух выборках проверяется гипотезао совпадении тольконекоторых параметров распределений.

Пусть F_n и G_m – эмпирические функции распределения, построенные по выборкам X и Y соответственно. Введём величину

. (4.6)

Если верна гипотеза H ₀ , то при увеличении объёмов выборок эмпирические функции распределения сходятся по вероятности к общему пределу, то есть D_n,m 0. То, с какой скоростью это происходит, показывает следующая теорема (без доказательства).

Теорема Колмогорова –Смирнова. Пусть верна гипотеза H ₀ и общая функция распределения двух выборок непрерывна. Тогда для любого y > 0 при n → ∞, m → ∞ .

Пусть q таково,что K (q) = 1 – ε. Положим критическое множество

, (4.7)

то есть мы отвергаем гипотезу об однородности, если расхождение между двумя эмпирическими функциями распределения достаточно велико. При больших n вероятность ошибки 1-го рода α =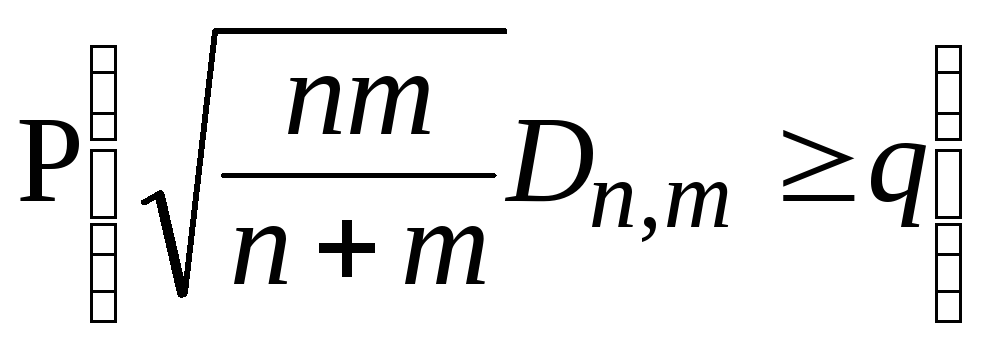≈1–K(q) ≈ ε.

b. Проверка гипотез о совпадении параметров распределений.

Рассмотрим задачу проверки согласия двух распределений, представленных своими выборками, на основе сравнения некоторых параметров этих распределений. Вообще говоря, все параметры практически употребляемых распределений выражаются через свои первые четыре момента. Однако, задача статистического сопоставления произвольных распределений даже на уровне двух первых моментов (проблема Беренса – Фишера) до сих пор не имеет общего решения. Поэтому далее предполагаем, что обе выборки извлечены из нормальных распределений, параметры которых, однако, неизвестны. К тому же, данная ситуация на практике встречается наиболее часто.

Проверка гипотезы о совпадении средних.

Особенно часто в приложениях встаёт вопрос о сравнении центров распределения двух нормально распределённых величин ξ и η. В таком случае полагаем (по основной гипотезе),что выборки X и Y извлечены из нормально распределённой генеральной совокупности.

В данном случае проверяется гипотеза

H ₀ : m₁ = m₂ против H₁ : m₁ ≠ m₂. (4.8)

При этом предполагается, что дисперсии теоретических распределений совпадают, хотя и не известны: неизвестно.

Для построения критерия используем выборочные средние и дисперсии

.

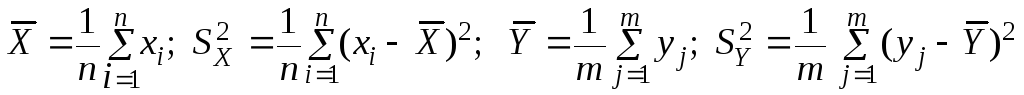В силу того, что инезависимы и распределены нормально:

N(m₁, σ²/n) = ; N(m₂, σ²/m) = ,формируем на их основе статистику, имеющую стандартное нормальное распределение:

Z = [–– (m₁ – m₂)]/{σ²(1/n + 1/m)}^1/2  N(0, 1). (4.9)

Также по свойству выборок из нормального распределения

nS_X²/σ₁²  ; mS_Y²/σ₂²  , (4.10)

причём эти случайные величины независимы, т. к. построены по независимым выборкам. Далее, по свойству распределения хи-квадрат, статистика

S² = (nS_X² – mS_Y²) / [σ²(n + m – 2)]  (4.11)

не зависит –и распределена похи-квадрат с (n + m – 2) степенями свободы. Таким образом, если верна гипотеза H₀ , то статистика

ψ = Z /S = (4.12)

имеет распределение Стьюдента с (n + m – 2) степенями свободы. По таблице распределения Стьюдента находим величину q такую, что (–q) =ε/2.Тогда P{–q < ψ <q } = (q) –(–q) = 1 –ε.Вероятность ошибки первого рода α = P{(x₁, …, x_n; y₁, …, y_m)  Κ} = ε, где критическая область

Κ = {(x₁, …, x_n; y₁, …, y_m) : | ψ | ≥ q }.

Проверка гипотезы о совпадении дисперсий.

Здесь проверяется основная гипотеза

H₀ : σ₁² = σ₂² против H₁ : σ₁² ≠ σ₁² . (4.13)

Из величин (4.9) можно построить случайную величину

η = nS_X²/(n – 1)σ₁² : mS_Y²/(m – 1)σ₂² = , (4.14)

имеющую распределение Фишера. С помощью таблиц этого распределения находят числа q₁ и q₂ такие, что (q₁) =ε/2; (q₂) =ε/2. Тогда

P{q₁ < η <q₂ } = (q₂)–(q₁)= 1 – ε.Гипотеза H₀ отвергается, если η (q₁ , q₂). Вероятность этого события (в предположении верности гипотезы H₀) в точности равна ε. Критическая область Κ = {(x₁, …, x_n; y₁, …, y_m) : η (q₁ , q₂)}.