Заключение

Задачи, решаемые методами математической статистики, не ограничиваются тем, что рассмотрены выше. В стороне остались практически весь факторный анализ, значительная доля дисперсионного анализа; довольно поверхностно рассмотрены проблемы регрессионного анализа, а некоторые разделы корреляционного анализа (корреляция категоризированных переменных, множественная и частная корреляция и регрессия) не подкреплены практическими задачами и носят лишь роль справочнрго характера (соответсвующий этим разделам материал помечен в оглавлении *). Совсем не затрагиваются теория статистических решений и теория эксперимента. Но скорее всего прав Козьма Прутков, утверждая, что «нельзя объять необъятное». Такая цель и не ставилась. Годовой курс теории вероятностей и математической статистики с элементами теории случайных функций, теории игр и массового обслуживания, для которого данный практикум и создавался, может включить в свой объём лишь основополагающие задачи математической статистики.

Основные теоретические положения и практические задачи теории случайных функций, простейший поток событий, марковские и пуассоновские процессы, основные типы СМО и элементы теории игр (в значительной степени использующей упомянутую выше теорию статистических решений) будут рассмотрены в 3-й, заключительной части данного пособия.

Разлел II вариаты практических заданий

1. Общие положения.

Выбор учащимися конкретного варианта в каждом конкретном случае определяется преподавателем (например, по порядку списка в учебном журнале). После определения номера варианта, порядок ваших действий таков:

В соответствии с заданным ниже для конкретного варианта алгорит-

мом, получить необходимое число случайных чисел, распределённых равномерно на интервале (0; 1). Формулы алгоритмов в основном определяют необходимое число таких чисел. Источник этих чисел – любой: таблица подходящих случайных чисел в каком-либо пособии; программа EXEL вашего ноутбука и т. п.

Пользуясь заданным для вашего варианта алгоритмом, получить (рассчитать) 100 чисел, которые в дальнейшем рассматриваются как полученная в результате некоего эксперимента выборка. Эта выборка, либо её элементы, используются при выполнении большинства заданий варианта. Вполне допустимо получать по заданной формуле разные выборки для разных заданий. Более того, по усмотрению преподавателя, можно в заранее регламентированном порядке менять формулы при получении различных выборок для различных заданий.

2. Алгоритмы – формулы расчёта выборок и предлагаемое их

распределение по вариантам.

Варианты 1  3: x_k = (ln R_k)/[ln(1 – p)], округлённому в большую сторону до ближайшего целого числа, k = 1, 2, …, 100; R_k равномерно распределены на (0, 1); параметр p = 0,25; 0,5; 0,75 – по вариантам.

Замечание: значения параметраp (0, 1) и могут быть выбраны другими.

Варианты 4  6: 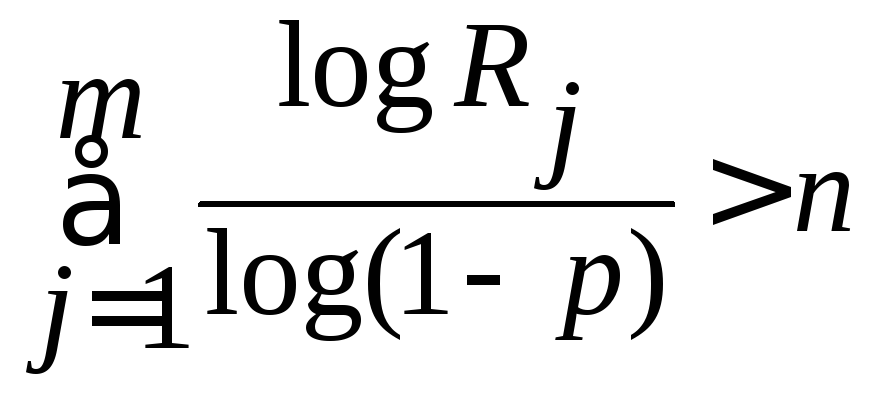;R_j равномерно распределены на (0; 1) , k = 1, 2, …, 100; основание логарифмов – произвольное (но лучше – e). Величину n принять равной 4; 6; 8 по вариантам.

Варианты 7  9: , k = 1, 2, …, 100. Достаточно 15 распределённых равномерно на (0; 1) чисел; индекс k при этом нумерует подмножество таких чисел, используемых для расчёта k – го выборочного значения.

Варианты 10  12: Две независимые случайные переменные (x_k)₁ и (x_k)₂ получаем из независимых, распределённых равномерно на (0; 1) чисел R_k, k = 1, 2, …, 100, с помощью соотношений:

(x_k)₁ = (– 2 ln (R_k)₁)²sin(2π(R_k)₂); (x_k)₂₁ = (– 2 ln (R_k)₁)²cos(2π(R_k)₂).

Минимально необходимо 51 равномерно распределённое число.

Варианты 13  15: x_k = a + c∙ln[R_k /(1 – R_k)] , где R_k – распределённые равномерно на (0; 1) числа; a и c – числовые параметры. Предлагаются следующие варианты: (a; c) = (0; 1); (0; (3)^1/2/π); (3; 2).

Варианты 16  18: 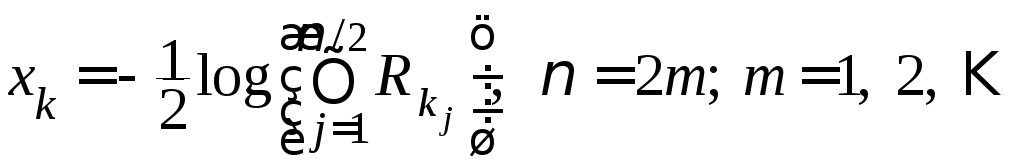, то есть при чётном параметре ν и , если ν = 2т – 1 , то есть при нечётном значении параметра. Для набора достаточного числа различных кортежей равномерно распределённых чисел, в самом худшем случае (ν = 4) достаточно 15 таких чисел. Параметр ν = 2; 3; 4 по вариантам.

Варианты 19  21: , где b = 1/λ и с – заданные параметры, причём с – целое число; R– распределённые равномерно на (0; 1) числа. Так как при вычислении очередного числа x_k в кортеже из c чисел R_j требуется хотя бы одно заменить новым, то для создания выборки объёма n = 100 потребуется как минимум (c + 99) равномерно распределённых чисел. Предлагаются следующие значения параметров (по вариантам): (c, b) = (1; 4); (2; 0,5); (2; 1).

Варианты 22  24: , где R_k – распределённые равномерно на (0; 1) числа, k = 1, 2, …, 100; a и b – числовые параметры. Предлагаются следующие варианты: (a; b) = (2; 1); (2; 3); (3; 2).

Варианты 25  27: , где R_k – распределённые равномерно на (0; 1) числа, k = 1, 2, …, 100; x₀ и с – числовые параметры. Предлагаются следующие варианты: (x₀; c) = (1; 3); (2; 4); (1; – 3).

Варианты 28  30: x_k = a + b∙ln|lnR_k|, где R_k – распределённые равномерно на (0; 1) числа, k = 1, 2, …, 100; a и b – числовые параметры. Предлагаются следующие варианты: (a; b) = (0; 1); (1; 1); (– 1; 2).

УПРАЖНЕНИЕ I.

Используется полученная указанным выше для вашего варианта способом или, соответственно, взятая из Приложения I выборка.

Задание 1.1. Первичная обработка выборочных данных.

Выполнить обработку совокупности данных в следующей последовательности:

1) упорядочить по величине значения переменной, представленную выборкой;

2) ранжировать и табулировать значения переменной;

3) выстроить простой вариационный ряд;

4) выстроить интервальный вариационный ряд;

5) произвести графическое представление распределения частот;

а) построить эмпирическую функцию распределения;

б) построить полигон распределения;

в) построить гистограмму распределения;

6) вычисление числовых выборочных характеристик распределения;

а) вычислить меры центральной тенденции: выборочную моду, выборочную медиану, выборочное среднее арифметическое;

б) вычислить характеристики рассеяния: размах, выборочную дисперсию, выборочное среднеквадратическое отклонение;

в) вычислить коэффициент вариации;

г) вычислить коэффициент асимметрии;

д) вычислить коэффициент эксцесса.

Задание 1.2. Полагая, что выборка получена из нормально распределённой генеральной совокупности с неизвестными математическим ожиданием и дисперсией, получить оптимальные доверительные интервалы для этих параметров с уровнем доверия: а) γ = 0,95; б) γ = 0,99.

Задание 1.3. Используя критерий согласия хи-квадрат Пирсона проверить гипотезу H₀ о том, что данная выборка получена из нормальной генеральной совокупности, параметры которой заданы только выборочными оценками математического ожидания и дисперсии. Критические значения критерия вычисляются при уровнях значимости γ₁ = 0,95 и γ₂ = 0,99.

Задание 1.4. Пользуясь методом однофакторного дисперсионного анализа провести проверку вашей выборки на однородность. Число градаций фактора рекомендуется положить равным 5 или 10. Обработке подлежит ваша первоначальная необработанная и неупорядоченная выборка.

Задание 1.5. Получить (на основе вашей выборки) указанными методами для указанных ниже распределений выборочные оценки соответствующих параметров:

— варианты 1 ÷ 3; параметр p геометрического распределения F(x) = 1 – (1 – p)^x (функция вероятности P{ξ = x}  f(x) = p(1 – p)^x), x  n методом максимального правдоподобия;

— варианты 4 ÷ 6; параметр p биномиального распределения с функцией вероятности , 0 <x < n, методом максимального правдоподобия;

— варианты 7 ÷ 12; параметры  и  нормального распределения с функция плотности вероятности f(x) = (2π²)^–1/2exp{(x - )²/2²}, методом максимального правдоподобия;

— варианты 13 ÷ 15; параметры a и c логистического распределения F(x) = 1 – {1 + exp[(x – a)/c]}^–1, методом максимального правдоподобия или методом моментов;

— варианты 16 ÷ 18; использовать заданный параметр ν как параметр хи-квадрат распределения f(x) = [(x^{(ν – 2)}/2^ν)^1/2/Γ(ν/2)]exp(– x/2);

— варианты 19 ÷ 21; параметры b и c (с округлением c до целого числа) гамма распределения f(x) = (x/b)^{c – 1}[exp((– x/b)]/b Γ(c), методом моментов;

— варианты 22 ÷ 24; параметр a и b распределения Вейбулла F(x) = 1– exp[–(x/b)^c], методом максимального правдоподобия или методом моментов;

— варианты 25 ÷ 27; параметры x₀ и c распределения Парето (или степенного при c < 0) f(x) = (c/x₀)(x/x₀)^{– (c – 1)}, методом максимального правдоподобия;

— варианты 28 ÷ 30; использовать заданные параметры a и b как параметры распределения экстремального значения F(x) = 1 – e^{– exp[(x – a)/b]}.

Во всех случаях, по критерию Смирнова проверить гипотезу согласия вашего выборочного распределения с распределением, параметры которого вы оценили. Критические значения для критерия Смирнова можно найти в соответствующей таблице Приложения IV.

Замечание: Задание 1.5 выполняется и в том случае, если используемая вами выборка не получалась на основе предложенных в разделе 2. алгоритмов, а взята из готовых (Приложение 1).

УПРАЖНЕНИЕ II.

Выбор статистического материала и его распределение, как и распределение заданий по вариантам задаётся в условиях каждой задачи. Необходимые данные приведены также в Приложении II. Все варианты выполняют все 5 задач.

Задача 1. Для контроля взяты 200 узлов, собранных на ученическом конвейере. Число узловm_i, при сборке которых пропущеноiопераций, сведено в таблицу:

i	0	1	2	3	4	5	6	7
mi	37	60	51	22	16	8	4	2	Всего 200

Согласуются ли по критерию ² с уровнем значимости α = 0,05 {²_0,05(7) = 14,07} полученные результаты с предположением о том, что случайное число пропущенных операций ξ распределена по закону Пуассона с плотностью , где параметра оценивается по выборочным данным: варианты 1 ÷ 10 – как среднее число пропущенных операций; варианты 11 ÷ 20 – как модальное значение числа пропущенных операций; варианты 21 ÷ 30 – как медианное значение числа пропущенных операций.

Задача 2. Тысяча человек участвовала в соревнованиях по рыбной лов-

ле. Из них m_iчеловек поймалиiрыб, что представлено первыми двумя строками следующей таблицы:

i	0	1	2	3	4	5	6	7	8	9	10
mi (A)	437	250	138	80	49	16	10	8	6	3	3
mi (B)	351	265	163	105	60	26	11	9	7	1	2
pi a=0,6	0,400	0,240	0,144	0,086	0,052	0,031	0,019	0,011	0,007	0,010
pi а*=?

С уровнем значимости α= 0,05 проверить гипотезу о показательном законе распределения случайной величины ξ, представляющем число пойманных рыб,. Решить задачу для заданного значения параметраa = 0,6 и для случая, когдаa оценивается по выборке:A длявариантов 1 ÷ 3,11 ÷13, 27 ÷ 30; Bдлявариантов 4 ÷ 6,14 ÷16, 23 ÷ 26; (A + B)/2 длявариантов 7 ÷ 10,17 ÷22.

Задача 3. Из генеральной совокупности случайной величины ξ, распределённой по: а) биномиальному законуP(ξ = k) = Р_n(k) = , (k= 0; 1; 2; …;n); б) по закону ПуассонаP(ξ = k) = Р_k =λ^k e^-λ∕k!, (k= 0; 1; 2; …); с) по закону ФариаP(ξ = k) = p(1 –p)^k, извлечена выборкаобъёмаm: {x₁;x₂;…;x_m} = (2, 6, 5, 0, 12, 10, 3, 6, 7, 9). Найти методом моментов и методом максимального правдоподобия статистическую оценку независимого параметраpи показать её несмещённость и эффективность.Варианты 1 + 3jиспользуютвыборку для распределения а);варианты 2 + 3j– выборку для распределения б);варианты 3j – выборку для распределение c), (j = 1, 2, … , 10).

Задача 4. Используя предельное распределение Колмогорова (критерий Колмогорова), найти приближенно уровень значимости выборки A против гипотезы Н₀. Дать его традиционную интерпретацию. Варианты 1–8, 14, 15, 17, 18, 20, 26, 29: Н₀ – равномерное распределение генеральной совокупности на отрезке от минимального значения выборки до максимального. Варианты 9 – 13, 16, 19, 21 – 25, 27, 28, 30: Н₀ – экспоненциальное распределение с параметром, совпадающим с оценкой по выборке.

Задача 5. Дискретная случайная величина ξ имеет распределениеP(ξ=x_m) = (1– a)a ^m,m = 1, 2, …, 10. Используяметод моментов и метод максимального правдоподобия, получить точечные оценки параметраa по выборочным данным:варианты 1 ÷ 10– по выборкеA;варианты 11 ÷ 20– по выборкеB;варианты 21 ÷ 30– по объединению выборокAиB.

Примечание: в качестве выборочного материала используется положительные значения последних цифр этих выборок.

УПРАЖНЕНИЕ III

Каждый вариант выполняет одну задачу. Предлагается: № варианта = № задачи (возможны и другие распределения задач).

Задача 1.При оценке качества изготовления деталей были получены выборочные оценки математического ожидания (выборочное среднее)= 43 мкм и несмещённой оценки дисперсии Ѕ² = 92,25 мкм²случайных отклонений от стандарта. Оценить, с надёжностью а) 0,95; б) 0,99, точность, с которой выборочное среднее аппроксимирует математическое ожидание.

Задача 2.Уровни воды в реке по отношению к номиналу измерялись в течении 44 весенних паводков и результаты измерений приведены в таблице:

Уровень (в см.)	0 – 100	100 - 150	150 - 200	200 - 300	300 – 400
Число случаев	10	13	9	8	4

Считая, что высота уровня ξ распределена по закону ² с плотностьюx=(х ≥ 0), с помощью метода моментов найти оценки параметрова иkэтого распределения.

Задача 3.При оценке качества изготовления деталей были получены по выборке объёмом n = 50 оценки математического ожидания (выборочное среднее)= 43 мкм и несмещённой оценки дисперсии Ѕ² = 92,25 мкм²случайных отклонений от стандарта. Оценить, с надёжностью а) 0,99; б) 0,95, точность, с которой выборочная несмещённая оценка дисперсии Ŝ²представляет дисперсию σ²генеральной совокупности.

Задача 4.В течении второй мировой войны на Лондон упало 537 самолётов–снарядов; вся территория Лондона была разделена на 576 равных по площади участка (по 0,25 км²); в таблице указаны числа участков n_i, на которые упало ν_i снарядов:

νi	0	1	2	3	4	5 и больше
ni	229	211	93	35	7	1

С помощью критерия ² проверить, с доверительной вероятностью а) 0,95; б) 0,99, согласуются ли эти данные с гипотезой о том, что числа снарядов распределены по закону Пуассона с параметром λ, за значение которого выборочное среднее.

Задача 5.В результате n = 10 опытов получена несмещённая оценка дисперсии Ѕ² = 18 нормальной случайной величины. Найти доверительный интервал для дисперсии при доверительной вероятностиP= 0,8.

Задача 6.Методом моментов и методом максимального правдоподобия найти оценку параметра λ распределения Пуассона по выборке {x_k} = {4, 6, 5, 3, 2, 1, 1}, объёма n = 22 и доказать её несмещённость и состоятельность.

Задача 7.Требуется определить при доверительной вероятности 0,96 доверительный интервал для дисперсии высоты штамповок внутренних колец подшипников по данным пробы объёмом n =20 штук, если распределение штамповок по высоте предполагается нормальным. Средняя арифметическая высота 20 колец= 32,2975 мм; выборочная оценки дисперсии Ѕ² = 0,1264 мм²; уровень значимости q = 4%.случайных отклонений от стандарта.

Задача 8.Определить доверительный интервал для оценки генерального среднего диаметра d валика по «пробе» из 10 деталей, обработанных на токарном автомате, если среднее арифметическое отклонений размеров деталей от середины поля допуска=2мкм и несмещённая оценка дисперсии Ѕ² = 5,29 мкм²; доверительная вероятность р=0,99.

Задача 9.Из распределения Коши с плотностью ƒ(x) = 1/π[1+(x– μ)²] извлечена выборка объёмаn; а) будет ли выборочное среднеесостоятельной оценкой модых_ти/или медианыμ_1/2этого распределения? б) пусть имеется какая-нибудь состоятельная и несмещённая оценка m медианы (например, выборочная медианах_1/2); указать нижнюю границу объёма выборки для того, чтобы дисперсия этой оценки не превосходила 0,01.

Задача 10.Проведено 5 независимых равноточных измерений для определения заряда электрона. Подучены результаты: |e |(10^–19Кл) =: 1,594; 1,597; 1,598; 1,593; 1,590. Определить доверительный интервал для оценки величины заряда электрона при доверительной вероятности 99% .

Задача 11.Проведено 5 независимых равноточных измерений толщины пластины. Подучены результаты: d(см) =: 2,15; 2,18; 2,14; 2,16; 2,17. Определить истинное значение толщины пластины с помощью доверительного интервала с доверительной вероятностью 1– α = 0,95 .

Задача 12. Дискретная случайная величина ξ имеет распределениеP(ξ=x_m) = (1– a)a ^m,m = 1, 2, …, 10. Используя метод моментов и метод максимального правдоподобия, получить точечные оценки параметраa по выборке (x₁, x₂, …, x₁₀) = (2, 6, 5, 0, 12, 10, 3, 6, 9, 7),

где параметр а оценивается по выборочным данным.

Задача 13. Из 35 новорождённых оказалось 18 мальчиков. Найти доверительный интервал для вероятностиp рождения мальчика при доверительной вероятности: а) γ = 0,95; б) γ = 0,99.

Задача 15. Сколько нужно получить безотказных срабатываний пожарной сигнализации, чтобы с доверительной вероятностью 0,99 утверждать, что вероятность отказа этой сигнализации не превышает а) 0,001; б) 0,005?

i	1	2	3	4	5	6	7	8	9	10	11	12
ni	7280	6957	7883	7884	7892	7609	7585	7393	7203	6903	6552	7132
pi				…	ЗА СТО	ПОЛ Я	НИТЬ ТЕ	СА ЛЬ	МО НО	…

Задача 16. По статистическим данным, в Швеции в 1935 г. родилось 88273 и дни рождения их известны. Если использовать естественное разбиение года на интервалы по месяцам (длина интервала – число дней месяца), то распределение переменнойX _i – номер дня рожденияi– го человека,i =1 ÷n = 88273, имеет вид:

На основании этих данных надо проверить гипотезу H₀:i P_i (X_i = k) =

=1/365, k = 1, …, 365, т.е. о равномерном распределении дней рождения по дням года по критерию: а) Пирсона χ²; б) Колмогорова с уровнем доверия

(1 – α) = 0.95.

Задача 17. При проведенииn=16 независимых испытаний с неизвестной вероятностьюp«успеха» в каждом испытании наблюдалосьk= 8 «успехов». Определить значения границ доверительного интервала для с уровнем доверияγ = 0,9.

Задача 18. Из большой партии электроламп было отобрано случайным образом 400 шт. для определения средней продолжительности горения. Выборочная средняя продолжительность горения ламп оказалось равной 1220 ч. Найти с коэффициентом доверия γ = 0,995 доверительный интервал для средней продолжительности горения электролампы по всей партии, если среднее квадратичное отклонения продолжительности горения равно 35 ч.

Задача 19. В результате пусков 10 ракет получены (в условных единицах) значения боковых отклонений точек попадания от точек прицеливания:

№ ракеты	1	2	3	4	5	6	7	8	9	10
Отклонение	1,0	0,2	1,0	-0,1	-0,5	5,0	-1,0	3,0	0,5	1,0

Полагая, что случайная величина ξ (случайное отклонение точек попа- дания от точек прицеливания) имеет нормальное распределение, построить доверительный интервал для её а) математического ожидания и б) дисперсии с коэффициентом доверия γ = 0,99.

Задача 20. Из партии однотипных высокоомных сопротивлений отобрано 10 штук. У каждого из них измерены отклонения сопротивления от номинального значения:

№ изделия	1	2	3	4	5	6	7	8	9	10
Отклонение	1	3	-2	2	4	2	5	3	-2	4

Предполагая, что контролируемый признак имеет нормальный закон распределения, определить выборочные значения параметров этого распределения и найти доверительный интервал для а) дисперсии и б) математического ожидания с коэффициентом доверия γ = 0,96.

Задача 21. При проведении 5 независимых равноточных измерений заряда электрона получены следующие результаты (в абсолютных электростатических единицах): 4,781; 4,792; 4,795; 4,779; 4,769. Определите значение оценки величины заряда электрона и найдите доверительный интервал для этой величины при коэффициенте доверия а) 95%; б) 99%, считая, что ошибки распределены по нормальному закону и измерения не имеют систематических ошибок.

Задача 22. На контрольных испытаниях осветительных 16 ламп были определены значения оценок математического ожидания и среднего квадратичного отклонения их срока службы: = 3000 ч. и σ = 20 ч. соответственно. Считая, что срок службы ламп имеет нормальный закон распределения, определите: а) доверительный интервал для математического ожидания при доверительной вероятности 0,9; б) вероятность, с которой можно утверждать, что абсолютная величина ошибки определенияmне превысит 10 ч.

Задача 23. Проведено 40 испытаний базы длинойL. По результатам опыта получены значения оценок математического ожидания и среднего квадратичного отклонения измеряемой величины: = 10400 (м) и σ = 85 (м). Ошибки измерения подчиняются нормальному закону распределения. Найти: 1) вероятность того, что неизвестный параметрLпопадёт в интервал со случайными границами (0,999; 1,001); 2) значение коэффициентаk, задающего границы доверительного интервала ± для величиныL при вероятности попадания в него 0,75.

Задача 24. По результатам 10 измерений ёмкости конденсатора прибором, не имеющей систематической ошибки, получили следующие отклонения от номинального значения (пФ):

5,4; -13,9; -11; 7,2; -15,6; 29,2; 1,4; -0,3; 6,6; -9,9.

Найти 90%-ный доверительный интервал для дисперсии и среднего квадратичного отклонения, предполагая, что генеральная совокупность имеет нормальное распределение.

Задача 25. По 15 независимым равноточным измерениям были рассчитаны значения оценок математического ожидания и среднего квадратичного отклонения максимальной скорости самолёта:v=424,7 м/с и σ_v= 7,7 м/с. Считая, что генеральная совокупность имеет нормальное распределение, определите: а) доверительный интервал для среднего квадратичного отклонения при доверительной вероятности 0,9; б) вероятность того, что абсолютная величина случайной ошибки при определении σ_v по 15 измерениям не превзойдёт 2 м/с.

Задача 26. Относительно некоторого измерительного прибора известно, что он не имеет систематических ошибок, а случайные ошибки измерения подчиняются нормальному закону распределения. Сколько надо произвести измерений для определения оценки среднего квадратичного отклонения прибора, чтобы с доверительной вероятностью 70% абсолютная величина ошибки определения этой величины была не более 20% от? Как изменится величина этой ошибки, если при том же числе измерений выставить 90%-й уровень доверия?

Задача 27. При проверке 100 деталей из большой партии было обнаружено 10 бракованных. Найдите: а) 95 %-й; б) 99 %-й доверительный интервал доли бракованных деталей во всей партии.

Задача 28.Из большой партии транзисторов одного типа были случайным образом отобрано и проверены 100 шт. Коэффициент усиления 36 транзисторов оказался меньше 10. Найдите: а) 95%-ный доверительный интервал для доли таких транзисторов во всей партии; б) доверительную вероятность, если доверительный интервал для доли таких транзисторов во всей партии будет (0,25; 0,5).

Задача 29.Произведено 20 бомбометаний с радиолокационным прицелом в примерно одинаковых условиях. Были получены следующие результаты измерения отклонений от центра цели (в метрах): 148; 182; 195; 81; 149; 143; 133; 132; 111; 156; 103; 61; 149; 209; 124; 52; 147; 145; 128; 98.

1. Полагая, что случайная величина – отклонение от центра цели – имеет нормальное распределение с неизвестными параметрами μ и σ², найти методом моментов точечные оценки параметров распределения по имеющейся реализации.

2. Рассмотрим случайное событие А, заключающееся в том, что величина отклонения от центра превышает 100 метров. Вероятность события А является неизвестной Р(А) = θ. Требуется найти оценку МП для неизвестной вероятности события.

Задача 30. У 20 телевизоров измерялась чувствительность звукового канала. Были получены следующие данные измерений (в микровольтах): 2,878; 1,400; 5,090; 2,929; 0,784; 3,260; 0,004; 1,490; 0,082; 1,708; 0,956; 3,241; 1,061; 2,375; 2,512; 2,110; 5,016; 0,601; 0,226; 1,166.

1. Полагая, что чувствительность звукового канала является случайной величиной, распределённой по показательному закону, найти методом моментов точечную оценку неизвестного параметра распределения по имеющейся реализации.

2. Найти точечную оценку неизвестного параметра распределения по имеющейся реализации методом максимального правдоподобия (МП).

УПРАЖНЕНИЕ IV.

Пользуясь индивидуальными для каждого варианта таблицами выборочного материала необходимо в каждом варианте выполнить все предлагаемые задачи (или какую-либо их часть – по усмотрению преподавателя).

Задача 1. По выборке A значений случайной величины ξ₁ найти несмещенные оценки математического ожидания Mξ₁ и дисперсии Dξ₁, оценки стандарт­ного отклонения σ и медианы. Какова стандартная ошибка оценки матема­тического ожидания?

Задача 2. По выборке A найти доверительные интервалы для математического ожидания и дисперсии случайной величины ξ₁ при доверительной вероят­ности γ.

Задача 3. Из партии b изделий извлечена бесповторная выборка объёмом n штук, из которых m оказались дефектными. Найти оценку процента де­фектных изделий в партии и ее стандартную ошибку.

Задача 4. По выборке A при уровне значимости α проверить гипотезу Н₀: Mξ₁ = a при альтернативной гипотезе Н₁: Mξ₁ * a. Каков уровень значимости данных?

Задача 5. По выборке A при уровне значимости α проверить гипотезу Н₀: Dξ₁ = b при альтернативной гипотезе Н₁: Dξ₁ ≠ b.

Задача 6. По выборкам A и B найти доверительный интервал для разности средних (Mξ₂ – Mξ₁) при доверительной вероятности γ, считая дисперсии равными.

Задача 7. По выборкам A и B при уровне значимости α₁ проверить гипотезу Н₀: Mξ₂ – Mξ₁ = с при альтернативной гипотезе Н₁: Mξ₂ – Mξ₁ ≠ c, считая дис­персии равными. Каков уровень значимости данных?

Задача 8. По выборкам AиB при уровне значимости 0,5 проверить гипотезу Н₀: Mξ₁ = Mξ₂ при альтернативной гипотезе Н₁: Mξ₁ ≠ Mξ₂, считая диспер­сии равными. Каков уровень значимости данных?

Задача 9. По выборкам A и B при уровне значимости α проверить гипотезу о ра­венстве дисперсий Н₀: σ₁² = σ₂² при альтернативной гипотезе Н₁: σ₂² > σ₁². Ка­ков уровень значимости данных?

Задача 10. По выборкам A и B при уровне значимости α проверить гипотезу о ра­венстве дисперсий Н₀: σ₁² = σ₂² при альтернативной гипотезе Н₁: σ₁² ≠ σ₂². Каков уровень значимости данных?

Задача 11. В серии из 100n выстрелов по мишени наблюдалось 100m попаданий. Найти приближенный доверительный интервал для вероятности p попада­ния в мишень при доверительной вероятности γ.

Задача 12. Пусть выборка A - наблюденные значения случайной величины ξ₁ а такое же число первых элементов выборки B – соответствующие наблюденные значения случайной величины ξ₂. Найти точечную оценку коэффи­циента корреляции Пирсона ρ величин ξ₁ и ξ₂. Каков уровень значимости данных против гипотезы Н₀: ρ = 0 (в пользу гипотезы Н₁: ρ ≠ 0)?

Задача 13. В условиях задачи 12 найти точечную оценку корреляционных отношений η₁² и η₂² величин ξ₁ и ξ₂. Каков уровень значимости данных против гипотезы Н₀: ρ² = η₁² = η₂² = 0 (в пользу гипотезы Н₁: регрессия может быть любой формы)?

Задача 14. В условиях задачи 12 найти оценку линейной функции регрессии ξ₂ на ξ₁ Построить ее график с 95% доверительными интервалами для пред­сказаний. Найти точечное и интервальное предсказание величины ξ₂ при значении ξ₁ равном max{A} + 3.

Задача 15.В условиях задачи 12 найти оценку коэффициента ранговой корреляции Спирмена. Аппроксимируя точное распределение распределением Стьюдента, проверить на уровне значимости (1 - γ) гипотезу Н₀: ρ_s(ξ₁, ξ₂) = 0, против односторонней альтернативы, на которую указывают данные. Каков дости­гаемый уровень значимости?

Задача 16.В условиях задачи 12 найти оценку коэффициента ранговой корреляции Кендалла. Аппроксимируя точное распределение статистики Кендалла нормальным распределением, проверить на уровне значимости (1 – γ) гипотезу Н₀: ρ_s(ξ₁, ξ₂) = 0, против односторонней альтернативы, на которую указывают данные. Каков дости­гаемый уровень значимости?

Задача 17. В условиях задачи 12 рассчитать выборочные оценки коэффициента корреляции r, а также корреляционных отношений e₁² и e₂². Используя полученные результаты, проверить на уровне значимости (1 – γ) гипотезу H₀ о том, что регрессия ξ₁ по ξ₂ (или регрессия ξ₂ по ξ₁) строго линейна. Альтернативная гипотеза утверждает, что регрессии могут быть любой формы.

Задача 18. Для контроля было взято 200 узлов, собранных на ученическом кон­вейере. При этом они распределились по числу пропущенных при сборке операций следующим образом:

Число операций	0	1	2	3	4	5	6	7
Число узлов	71	45	32	22	16	8	4	2

Согласуется ли эти данные по критерию ² при уровне значимости α с экспоненциальным распределением с параметром d для случайного числа пропу­щенных операций? Параметры d и α выбираются по таблицам вариантов в столбце параметров П.

Указание:последние 2 интервала следует объединить.

Задача 19. Пользуясь критерием инверсий проверить гипотезу случайности корте­жа: выборка A, продолженная упорядоченной в порядке возрастания вы­боркой B (т. е. оценить уровень значимости и дать его традиционную ин­терпретацию.). Каков уровень значимости, рассчитанный по статистике для большой выборки?

Задача 20.По ранговому критерию Уилкоксона (Манна – Уитни) проверить на уровне значимости (1 - γ) гипотезу однородности выборок A и B при дву­сторонней альтернативе. Каков уровень значимости, рассчитанный по нор­мальной аппроксимации статистики критерия?

Указание: Исходные данные и параметры для задач этого упражнения содержатся в таблицахПриложения II.

УПРАЖНЕНИЕ V

Используя предлагаемые ниже варианты корреляционных таблиц необходимо: 1) определить точечные выборочные оценки коэффициентов корреляции Пирсона ρ, коэффициентов обеих линейных регрессий α₁, α₂, β₁, β₂; корреляционных отношений η₁² и η₂² случайных величин ξ₁ и ξ₂; 2) рассчитать доверительные интервалы для указанных величин; 3) найти оценку линейных функций регрессии ξ₂ на ξ₁ и ξ₁ на ξ₂; построить их график с 95% доверительными интервалами для пред­сказаний.; 4) проверить на уровне значимости (1 - γ) = 0,05 гипотезы наличия/отсутствия (Н₀: ρ = 0 против гипотезы Н₁: ρ ≠ 0) и линейности/нелинейности (гипотеза Н₀: ρ² = η₁² = η₂² = 0 против гипотезы Н₁: регрессия может быть любой формы) корреляции.

Указание: При выполнении упражнения можно воспользоваться результатами, полученными при выполнении задача 8 второго ИДЗ части I данного Практикума.

В качестве вариантов даны выборки из законов распределения двумерной случайной величины (ξ, η) (в виде таблицы) в Приложении III.