Методическое пособие Теория информации-2

где – средний квадратичный эффект (мощность) передаваемого сигнала.

Учитывая выражения (4.58) и (4.59), максимальную скорость передачи информации по каналу с ограниченной средней мощностью и случайным шумом можно определить следующим образом:

ÖSÒÁ

$lim→

log 2 `

5

log 2 `

log

(4.60)

∞

Рассмотрим случай, когда присутствующий в канале

связи шум носит

5

произвольный

характер. Предположим, что шум как и в предыдущем случае

складывается с сигналом линейно. Пусть

– средний квадратичный эффект

Ë

5

средний квадратичный эффект шума;

(мощность) передаваемого сигнала,

–

–

энтропийная мощность

шума.

Средний

квадратичный

эффект

5

loga2π`( + 5)b

в единицу времени для сигнала,

принимаемого

сигнала будет

равен

. Энтропия в единицу времени

принимаемого сигнала не может

превосходить

–

энтропию

+ 5

распределение

которого

совпадает с

log(2π`5)

распределением случайного шума. Энтропия произвольного шума в единицу

времени может быть определена, как

.

Тогда скорость передачи

значения, достигаемого в том

информации не может превышать максимального Ë

случае, когда принимаемому сигналу придают характеристики случайного шума:

Ö ≤ log 2 ` 5	log 2 `5 log
			5	(4.61)
Передаваемый сигнал	всегда можно наделить	свойствами случайного
			Ë

	loga2π`( + 5)b
шума, в этом случае энтропия в единицу времени для принимаемого сигнала
составляет как минимум		Ë . Тогда справедливо выражение:
ÖSÒÁ ≥ loga2π`( + 5)b −		log(2π`5) = log
			5	(4.62)
Формулы (4.61) и (4.62)		определяют верхний и Ëнижний пределы

наибольшей скорости передачиÖинформации по каналу связи с произвольным шумом. Фактическое значение SÒÁ определено только для случаев случайного

101

игауссовского шумов. Для случайного шума верхний и нижний пределы (4.61)

и(4.62) совпадают. Если мощность сигнала велика по сравнению с мощностью шума, то скорость передачи при любом характере шума приближается к следующему значению:

ÖSÒÁ ≈ log c Ëd
5	(4.63)

Выражение (4.63) показывает, что самое сильное влияние на пропускную способность канала связи оказывает шум, обладающий наибольшей энтропийной мощностью. Следовательно, при заданной мощности в заданной полосе частот наиболее вредным оказывается случайный шум, так как он обладает наибольшей энтропийной мощностью.

Рассмотрим скорость передачи информации по каналу с гауссовским

шумом. Гауссовский шум характеризуется нормальным распределение вероятностей значений сигнала в точках отсчета на оси частот и отсутствием взаимных связей между этими значениями. От случайного шума гауссовский шум отличается неравномерностью спектра и тем, что спектр не обязательно начинается от нулевой частоты. Случайный шум при помощи фильтра может быть переведенý(²в)гауссовский.

Пусть – функция спектральной плотности мощности полезного сигнала, тогда полная мощность сигнала:

= • ý(²) d²	(4.64)
'
Аналогично определим полную мощность шума:
5 = • (²) d²	(4.65)
'

	(²)
Разделим весь частотный диапазон на узкие полосы таким образом, чтобы
в пределах каждой полосы функция		была примерно постоянной. Для того,
	102

чтобы скорость передачи информации по каналу связи была максимальной,

полезный сигнал также должен обладать свойствами гауссовского шума. В

∆²этом случае энтропия∆²суммыlog·2π`полезногоaý(²)∆² +сигнала(²)∆²иb¸шума в узкой полосе частот ∆² logсоставляет·2π`a (²)∆²b¸ , а энтропия шума –

. Скорость передачи информации в узкой полосе частот

равна:

Ö∆ = ∆² log ˆ				‰	(4.66)
Поскольку связи между	значениями(		сигналов)		в отдельных точках отсчета
		²

на оси частот отсутствуют, общая скорость передачи информации находится

суммированием Ö∆ по всем ∆²:

Ö = • log

ˆ

ý(²) + (²)

‰ d²

(4.67)

'

(²)

Определим спектр мощности полезного сигнала, при котором при

максимальной.

(²)

и

заданной спектральной

плотности

заданной

полной

мощности сигнала

мощности

гауссовского шума

скорость передачи информации

будет

ÖSÒÁ = • log ˆ

ý(²)

+ (²)

‰ d² =

(

'

(²)

(

= • logaý(²) + (²)b d² − • loga (²)b d² =

(4.68)

'

(² − ² ) log c− 1d

'

=

− •( loga (²)b d²

(²

λ

'

, 5, (² − ² )

и

− ² ) log @−

Aот спектрального

распределения

.

103

константа,

зависящая

(²)

Выражение

–

только от

не

зависящая

	¶		log (²)b d²			является такой гауссовский	шум, при	котором
Следовательно,				наихудшим
интеграл		'(		a	,	характеризующий полную	мощность	шума,

1

максимален. Таким шумом является белый гауссовский шум:

(²) = − λ = Ì ý

4.3.2. Скорость передачи информации для сигналов с ограниченной пиковой

мощностью

•

Определим максимальную энтропию ансамбля с ограниченной пиковой

å

мощностью в точках отсчёта. Пусть пиковая мощность не превышает величины

во всех точках отсчёта, т.е. значения сигналов лежат между –

и +

•.

Энтропия сигнала будет максимальной в том случае, когда функция√

распределения вероятностей во всех точках постоянна в пределах от – √•

до

+å

и равна

√ð

. Соответственно, энтропия в каждой точке отсчёта равна:

O(°) = − • <(°) log <(°) d° = − –•

1

log

1

d° =

(4.69)

= −

1

log

1

√ð 2√•

2å

2√• = log 2√• = 1 log 4•

2å

2å

Вычислим энтропию ансамбля с пиковой2мощностью, ограниченной не

только в точках отсчёта, но и на всем интервале

. Если сигнал, рассмотренный

ранее и

описываемый

¤¥¦( “Œ&)

, пропустить

через

фильтр,

коэффициент

² =

равен единице и далее падает линейно, обращаясь

передачи которого при

“Œ&

¤¥¦ (“Œ&)

в ноль при

, то

получим сигнал, пиковая мощность которого ограничена

² = 0

(“Œ&)(

на всем

интервале

и

который описывается

функцией

(

.

В

соответствии с теоремой отсчётов, всякий сигнал с ограниченной пиковой мощностью в точках отсчёта может быть записан в виде ряда Фурье

104

$Œ		¤¥¦( “Œ&’ “), где	!
Q#									å
				– минимальное линейное значение сигнала в
-ой точке отсчёта, которое не превосходит по						абсолютному значению . На
∑	!	“Œ&’ “			∑ $Q#Œ
							@“Œ&’-(
выходе из фильтра сигнал будет равен								A(
						- ¤¥¦(@“Œ&’-( A. Сомножители

под знаком суммы в этом выражении не меняют своего знака во времени и

всегда совпадают по знаку с

. Выходной

сигнал

принимает своё

значение

+å

когда

все

+å

оказываются максимальными и

максимальное значение тогда,

!

равными

. Если входной сигнал

постоянен и равен

, то максимальное

!

выходного сигнала будет достигнуто при

и будет равняться .

На остальном диапазоне значение выходного

сигнала будет уменьшаться, что

² = 0

•

удовлетворяет условию ограничения пиковой мощности на всём интервале .

Энтропия в единицу времени для входного сигнала равна:

I	(4.70)

Энтропия в единицу времени для выходного сигнала равна:

O = log 4• + • log c

d d² = log 4• − 2 = log

`

(4.71)

#

Энтропийная мощность выходного сигнала равна:

c

d =

Ë

(4.72)

мощность

шума

составляет

,

Ë

Если

энтропийная 2π`

`

2π`

то энтропийная

меньше

мощность

принимаемого

сигнала

не может быть

5

;ð

+5

, что

соответствует энтропии в единицу времени, равной

“¡

O ´ = log 2π` c2π`

+ 5d .

(4.73)

Следовательно, скорость передачи информации будет равна:

105

Ö = O ´ − OÁ ´ = log 2π` c		2π`		+ 5d − log 2π`5 =	(4.74)
= log c	4•		Ë	+ 1d
	2π` 5

Энтропия ансамбля функций с ограниченными пиковыми значениями может быть оценена как величина, лежащая между значениями,

определяемыми выражениями (4.70) и (4.71).

4.4. Фильтрация

4.4.1. Классификация фильтров

Фильтры предназначены для выделения или ослабления сигналов с заданным спектром частот. В общем случае фильтром можно назвать частотно– зависимый усилитель, коэффициент усиления (пропускания) которого различен на разных частотах. Область частот, в которой фильтры обладают малым ослаблением сигнала (т.е. пропускают его), называется полосой пропускания.

Область частот, в которой фильтры существенно ослабляют сигнал, называется полосой заграждения (подавления, задерживания).

Фильтрация сигнала обычно предпринимается с целью увеличить отношение полезного сигнала к шумам и помехам или усилить полезные качества сигнала. Фильтры могут быть классифицированы в зависимости от вида входного и выходного сигналов, от вида частотной характеристики, от вида и длительности импульсной характеристики.

По виду входного и выходного сигналов фильтры подразделяются на аналоговые, цифровые, аналоговоцифровые (вход аналоговый, выход цифровой) и цифроаналоговые (вход цифровой, выход аналоговый).

По виду частотной характеристики фильтры разделяют на:

∙фильтры нижних частот (ФНЧ), которые пропускают низкочастотные составляющие спектра и задерживают высокочастотные;

∙фильтры верхних частот (ФВЧ), которые пропускают только высокочастотные составляющие;

106

∙фильтры полосно-пропускающие (ФПП), которые пропускают составляющие сигнала только в определённой полосе частот;

∙фильтры полосно-заграждающие (ФПЗ), которые пропускают все составляющие сигнала, за исключением тех, частоты которых входят в определённую полосу;

∙фильтры всепропускающие (ФВП), которые пропускают все составляющие сигнала, но изменяют фазовые соотношения между ними;

∙гребенчатый фильтр, который имеет несколько полос пропускания.

Перечисленные фильтры являются основными, но существуют и другие

разновидности. Графики амплитудно-частотных характеристик данных

фильтров представлены на рис. 4.5.

Рис. 4.5. Амплитудно-частотные характеристики фильтров:

а – нижних частот; б – верхних частот; в – полосно-пропускающий; г – полосно-

заграждающий; д – всепропускающий; е – гребенчатый

В качестве базового при анализе и синтезе фильтров используется фильтр нижних частот. Так, например, если из полного сигнала вычесть выходной сигнал ФНЧ, то получим ФВЧ (рис. 4.6а). ФПЗ можно построить, если включить параллельно ФНЧ и ФВЧ с разными полосами среза (рис. 4.6б).

Для построения ФПП достаточно соединить последовательно соответствующим образом рассчитанные ФНЧ и ФВЧ.

107

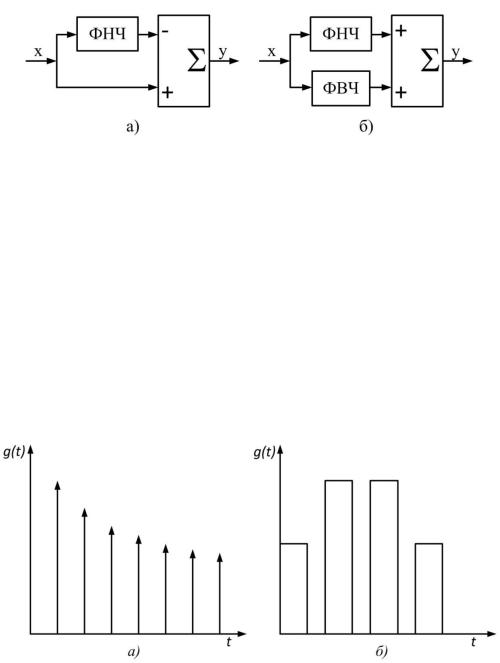
Рис. 4.6. Возможные структуры фильтров:

а– верхних частот; б – полосно-заграждающий

Взависимости от вида импульсной характеристики фильтры подразделяются на непрерывные, дискретные (импульсные характеристики фильтра представляют собой набор δ– импульсов, (рис. 4.7а) и импульсные

(импульсные характеристики фильтра представляют собой последовательность

одинаковых по форме импульсов конечной длительности разной амплитуды,

(рис. 4.7б).

Рис. 4.7. Импульсные характеристики фильтров:

а– дискретного; б – импульсного

Взависимости от длительности импульсной характеристики фильтры разделяют на фильтры с конечной импульсной характеристикой (КИХ),

импульсная характеристика которых ограничена во времени, и фильтры с бесконечной импульсной характеристикой (БИХ), импульсная характеристика которых хотя и затухает со временем, но теоретически имеет неограниченную длительность во времени.

108

4.4.2.Свойства линейных фильтров

Вустановившимся режиме свойства линейного фильтра определяются его комплексной функцией передачи ω :

(4.75)

где

| | =

‹

+ • = `Ò

φ = ,ÊÌ @ÕðA.

Если на вход линейного фильтра подаётся синусоидальный сигнал

частоты ω

и амплитуды , то откликом фильтра будет синусоидальное

колебание

той же частоты; амплитуда этого колебания будет равна

,

⁄2π

на угол

при этом выходной сигнал будет опережать входной сигнал по фазе| (ω )|

∙

(ω)

‚( )

φ(ω )Свойства.

фильтра можно характеризовать не только функцией передачи

, но и её обратным преобразованием Фурье

, определяемым

по

формуле:

‚( ) = 2π ’•

(ω)`

i•&

dω

(4.76)

‚( )

∞

δ( )

∞

∞

Функция

называется импульсным откликом фильтра и определяет

отклик фильтра на единичный импульс

в соответствии с уравнением:

δ( ) = 2π ’• `

i•&

dω

(4.77)

∞

Используя преобразование∞Фурье, выразим (ω) через ‚( ).

(ω) = • ‚( )`

’i•&

d

(4.78)

∞

Стоит отметить, что

’ (ω)

характеризует

поведение

фильтра

в

109

стационарном режиме, а					характеризует переходный процесс.
	Импульсный	отклик				представляет	собой		отклик фильтра на
				‚( )
единичный импульс,			переданный в момент времени						. Так как свойства
					‚( )	‚( − )
=							импульс,		поданный в момент
фильтра постоянны во времени, то единичный								= 0
	, вызывает на выходе отклик					. Поскольку фильтр линеен, к нему

применим принцип суперпозиции, т.е. отклик фильтра на сумму нескольких сигналов совпадает с суммой откликов на каждый из этих сигналов. Если на

вход подаётся сигнал		, то его можно рассматривать, как сумму узких
прямоугольных	импульсов высоты			и ширины		, относящихся к
		²( )	)		d
различным моментам времени (рис. 4.8)²(.

Рис. 4.8. Представление функции в виде последовательности импульсов

Каждый из прямоугольных импульсов									даст на выходе свой отклик
	( )			′						²( )
в последующий момент .					Согласно	принципу суперпозиции, полный отклик
								²( )d
фильтра	′	в	момент		времени		′	на весь сигнал			находится

суммированием откликов фильтра на все импульсы, поданные на его вход до

момента времени ′.

′

∞

− ) d

(

) = • ²( )‚(

− ) d = • ²( )‚(

(4.79)3

′

’

′

’

′

∞

′

∞

виду: Введя замену

τ = − , преобразуем уравнение (4.79) к следующему

>

‚( − ) = 0

3 Для существующих фильтров при

отклик на выходе

ã

верхний предел интегрирования может бытьã

расширен.

, следовательно,

110