
Методическое пособие Теория информации-2
.pdfвектор должен содержать только одну ненулевую вектор-строку, минимальный вес которой равен 2. Проверка на чётность каждого из ненулевых столбцов также даёт вектор веса 2. Следовательно, минимальный вес ненулевого вектора
итеративного кода с двойной проверкой на чётность равен
2 2 = 4.
Аналогично можно показать, что в общем случае минимальный вес вектора итеративного кода равен произведению минимальных весов векторов итерируемых кодов. Так как минимальное кодовое расстояние для линейного кода равно минимальному весу его ненулевых векторов, то минимальное расстояние итеративного кода равно:
n = ²© n© |
(6.51) |
где n³ – минимальное кодовое расстояние |
линейного кода по |
координате γ. |
|
Коррекция ошибок проводится последовательно. Сначала исправляют
ошибки по одной координате, затем оставшиеся ошибки исправляют по другой координате и т.д. Такая процедура проста, но снижает корректирующую способность итеративного кода, поскольку оказывается невозможным исправить часть ошибок кратности n − #/2 .
Пример. Пусть имеется неизбыточный двоичный код, длина кодовой |
|
комбинации которого |
= = 9. Пусть кодируемое сообщение имеет вид: |
100111011. Для построения двухмерного кода с проверкой на чётность разобьём кодовую комбинацию на три отрезка по три элемента в каждом и составим из них матрицу, дополнив её элементами, расчитанными по формулам
(6.45)-(6.47), – рис. 6.21.
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
Рис. 6.21. Матрица итеративного кода
201
Тогда передаваемая кодовая комбинация преобразуется к следующему виду: 1001111101100000 (избыточные символы выделены полужирным шрифтом). Даннаяn комбинация имеет результирующее минимальное кодовое расстояние % = 4. Она передается в канал связи строка за строкой. После приёма комбинации она снова представляется в виде матрицы.
Если код используется только в режиме обнаружения ошибок, он может обнаружить любую ошибку кратности от 1 до 3 по нарушению чётности в строке или столбце. Если код используется в режиме исправления ошибок, он может исправить любую одиночную ошибку (x = 1). При этом ошибочный символ будет находиться на пересечении той строки и того столбца, в которых обнаружены нарушения чётности.
Пусть при передаче произошло искажение последовательности. На рис. 6.22 представлены несколько возможных вариантов.
1 |
0 |
|
0 |
1 |
|
1 |
0 |
|
0 |
1 |
|
1 |
1 |
|
0 |
1/0 |
|
0 |
0 |
|
1 |
1 |
1 |
1 |
|
1 |
1 |
|
1 |
0 |
|
1 |
1/0 |
|
0 |
1 |
|
0 |
1 |
|
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
0 |
|
0 |
1 |
|
1 |
0 |
|
0 |
1 |
|
1 |
0 |
|
1 |
1 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
|
0 |
0/1 |
|
0 |
0 |
|
0/1 |
0/1 |
|
0/1 |
0 |
|
0 |
0 |
|
0 |
0 |
|
|
а |
|
|
|
|
б |
|
|
|
|
в |
|
|
|
|
г |
|
||||
Рис. 6.22. Принятое сообщение: а – ошибок нет; б – одна ошибка в сообщении,
которая может быть исправлена; в – три ошибки, которые могут быть обнаружены;
г – необнаруживаемые ошибки
Если ошибка окажется в символах контроля чётности, то нарушится лишь одно условие чётности. Для построения кода с исправлением двух, трёх и более ошибок необходимо сделать дополнительную проверку на чётность, например,
по диагоналям. Вводя такую проверку на чётность, можно построить самокорректирующийся код с большей надёжностью.
Пример. Рассмотрим итеративный двумерный код, представленный на рис. 6.23. Информационные символы обозначены ‰˜,. Каждая строка и столбец дополнены символом проверки на чётность ]˜ и • , соответственно. Каждая строка полученного блока дополняется символом , обеспечивающим
202
преимущества, так как предоставляет большие возможности для использования вводимой избыточности.
Рекуррентными эти коды называются потому, что соотношения,
связывающие проверочные символы с информационными, справедливы для любого участка информационной последовательности. В свёрточных кодах (как и в блочных), выделяют классы систематических и несистематических кодов (в
словах систематического кода известны позиции с информационными и проверочными символами).
Термин свёрточные коды объясняется тем, что кодовое слово можно рассматривать как свертку отклика линейной системы (кодера) и входной информационной последовательности. Поэтому свёрточные коды являются линейными, для которых сумма любых кодовых последовательностей также является кодовой последовательностью. В общем случае свёрточному кодированию могут подвергаться последовательности символов, являющихся элементами произвольного конечного поля ŒŽ • .
В данном пособии ограничимся рассмотрением двоичных свёрточных кодов. Принцип кодирования заключается в следующем: в каждый дискретный момент времени на вход кодирующего устройства поступают
P информационных последовательностей символов, а с его выхода в канал связи выдаются N последовательностей, причём N > P. Проверочные символы,
как и в блочных кодах, получаются в результате проведения линейных операций над определёнными информационными символами. Поскольку объём запоминающих устройств кодера ограничен, то влияние информационного символа на проверочные будет распрастронятся на конечное число позиций.
Назовём длиной кодового ограничения величину ´ = µP, где µ – число кадров,
хранящихся в кодере. Число позиций между информационным символом и максимально удалённым зависимым от него проверочным символом называется кодовой длиной блока и определяется как T = µ + 1 ∙ N .
Вследствие того, что проверочный символ зависит от информационных
204
символов из µ + 1 кадров, для построения хороших свёрточных кодов не
требуется увеличивать длину элементарного блока. Это определяет основное отличие свёрточных кодов от блочных и их достоинства.
Для получения слова систематического кода надо по известным
информационным символам найти проверочные символы и расположить их на |
||||||||
заданных позициях элементарного блока. Для простоты положим |
P = 1, т.е. |
|||||||
будем кодировать |
одну |
последовательность |
информационных |
символов |
||||
‰*, ‰ , ‰>, … ‰ B , ‰ , …, |
которая |
представляется |
в |
общем |
виде |
|||
многочленом: |
|
> |
B |
|
|
|
|
|
* |
|
|
|
(6.53) |
||||
|
|
|
|
|
|
|
|
|
Требуется найти последовательности проверочных символов, которые также можно описать многочленами:
y> = ›>** + ›> + ›>>> > + + ›>,BB B + ›> + |
|
|||||
|
|
|
…….. |
|
|
(6.54) |
y B = › B ,* + › B , + › B ,> > + + › B , B B + |
|
|||||
|
|
|
+› B , |
+ |
|
|
Последовательность проверочных символов y˜ |
находится с помощью |
|||||
порождающего многочлена: |
˜,%B |
˜% |
|
|||
˜ |
˜* |
˜ |
˜> |
(6.55) |
||
|
|
|
|
|
|
|
по формуле: |
|
|
˜ |
˜ |
|
|
|
|
|
|
(6.56) |
||
Отсюда |
следует, |
что проверочный символ |
›˜ является свёрткой |
|||
информационной последовательности и коэффициентов порождающего многочлена:
˜ |
* |
B |
> B> |
% B% |
(6.57) |
|
|
|
|
|
|
|
|
|
205 |
|
|
N − 1 |
Для задания |
всех проверочных последовательностей требуется |
|
порождающий |
многочлен. Максимальная степень многочлена |
= |
|
определяет число кадров, хранимых в кодере, т.е. длину кодового ограничения. |
||||||||
Если |
кодируется |
P |
информационных |
последовательностей |
||||
m , m> |
, … , mQ |
, то |
|
|
|
|
|
|
|
|
|
систематический свёрточный код со скоростью Q |
|||||
задаётся |
с |
помощью |
P N − P |
порождающих |
многочленов, |
а |
||
несистематический – |
с помощью PN многочленов. |
|
|
|||||
Пример. Пусть требуется применить простейший систематический |
||||||||
свёрточный код с параметрами: P = 1, N = 2, кодовым ограничением µ = 2, |
||||||||
скоростью Q = > |
бит на один символ. Кодовое слово является полубесконечной |
|||||||
последовательностью символов: |
B |
B |
|
|
||||
|
|
* * |
|
> > |
(6.58) |
|||
состоящей из элементарных блоков ‰ › . |
|
|
|
|||||
Порождающий многочлен этого кода будет M = M* + M = 1 + . С |
||||||||
помощью |
заданного |
многочлена |
M |
найдём проверочные символы |
для |
|||
следующей информационной последовательности, взятой в качестве примера: |
|||
‰* = 0, ‰ = 1, ‰> = 0, ‰c = 1, ‰8 = 1, …, которая |
описывается |
многочленом |
|
m = + c + 8 + . В соответствии с выражением (6.54) получим: |
|||
= + > + c |
+ , |
|
(6.59) |
|
|
||
что соответствует следующим |
значениям |
проверочных |
символов: |
›* = 0, › = 1, ›> = 1, ›c = 1, ›8 = 0, … |
|
|
|
Тогда, поступившая в кодер |
последовательность символов 01011… |
||
преобразуется кодером в следующую последовательность символов (жирным
начертанием отмечены информационные символы)
00 11 01 11 10 …
Пример. Пусть дан несистематический сверточный код с параметрами
206

P = 1, N = 2, скоростью Q = >, кодовым ограничением µ = 2. В случае
несистематического кода кодовое слово состоит из блоков, не содержащих информационные символы.
Для кодирования |
используем |
многочлены |
M = 1 + + > и |
|||
M> = 1+ >. Первые |
символы |
каждого |
блока |
являются |
свёрткой |
|
информационной последовательности и многочлена M , а вторые – |
свёрткой |
|||||
той же последовательности и многочлена M> |
. Заметим, что если один из |
|||||
многочленов приравнять 1, то получим систематический свёрточный код. |
||||||
Для поступающей в кодер информационной последовательности |
||||||
символов 01100… ( m |
= + > + ) получим: |
|
+ |
|
||
›> = + > |
+ 1+ > = + > + c + 8 |
(6.60) 3 |
||||
|
|
|
|
|
|
|
Тогда на выходе из кодера будет получена следующая
последовательность символов: 00 11 01 01 11 …
Свёрточный кодер как конечный автомат с памятью описывают диаграммой состояний. Диаграмма состояний представляет собой направленный граф, вершины которого отождествляются с возможными состояниями кодера, а ребра, помеченные стрелками, указывают возможные
переходы между состояниями. Состояние 000…0 называется нулевым;
остальные – ненулевые. Над каждым из ребер записывают кодовые символы,
порождаемые кодером при соответствующем переходе из состояния в состояние. На примере несистематического свёрточного кода рассмотрим построение диаграммы состояния кодера. Такой кодер будет содержать µ + 1
разрядов регистра, первые µ = 2 из которых описывают внутреннее состояние кодера. Первые два разряда регистра кодера могут находится в одном из
четырех состояний – 00, 10, 01, 11, которые будут соответствовать вершинам
3 Следует помнить, что суммирование одинаковых членов проводится по модулю 2, т.е. в |
|
уравнении (6.60) 1 ∙ > + 1 ∙ > = 0 ∙ >. |
207 |
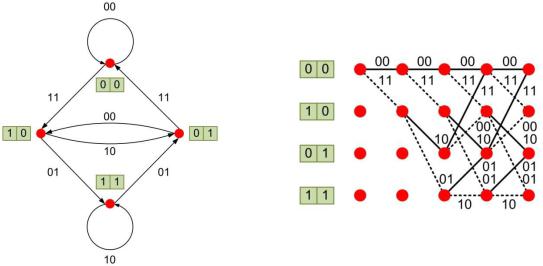
графа (рис. 6.24а).
а |
б |
Рис. 6.24. Диаграмма состояния кодера (а) и кодовая решётка (б)
Первоначально кодер находится в состоянии 00 и поступление на вход
символа 0 переводит его также в состояние 00, при этом все три разряда
регистра будут содержать 000 (здесь и далее жирным начертанием выделены
новые символы, поступающие в кодер). Первый выходной символ будет
определяться суммированием символов по модулю 2 |
во всех трёх разрядах, в |
||
соответствии с определяющим многочленом |
= 1 + + >, т.е. 0 0 |
||
0 =«n 2 = 0 |
; второй – суммированием по модулю 2 |
символов, содержащихся |
|
|
M |
|
|
в первом и третьем разряде, в соответствии с многочленом M> = 1+ >, т.е.
0 0 =«n 2 = 0 .
При поступлении на вход символа 1 кодер переходит в состояние 10, при
этом все три разряда регистра будут содержать 100. Первый выходной символ будет 1 0 0 =«n 2 = 1 ; второй – 1 0 =«n 2 = 0 .
Рассмотрим теперь ситуацию, когда кодер находится в состоянии 10.
Поступление на вход символа 0 вызовет переход кодера в состояние 01, при
этом в регистре будет храниться последовательность 010, а выходные символы будут 0 1 0 =«n 2 = 1 и 0 0 =«n 2 = 0 . Поступление на вход
символа 1 вызовет переход кодера в состояние 11, при этом в регистре будет
208
храниться последовательность 110, а выходные символы будут 1 1
0 =«n 2 = 0 и 1 0 =«n 2 = 1 .
Пусть кодер находится в состоянии 11. Поступление на вход символа 0
вызовет переход кодера в состояние 01, при этом в регистре будет храниться последовательность 011, а выходные символы будут 0 1 1 =«n 2 = 0 и 0 1 =«n 2 = 1 . Поступление на вход символа 1 не вызовет переход кодера
в новое состояние; при этом в регистре будет храниться последовательность 111, а выходные символы будут 1 1 1 =«n 2 = 1 и 1 1 =«n 2 = 0 .
Рассмотрим последнее возможное состояние кодера 01. Поступление на вход символа 0 вызовет переход кодера в состояние 00, при этом в регистре будет храниться последовательность 001, а выходные символы будут 0 0 1 =«n 2 = 1 и 0 1 =«n 2 = 1 . Поступление на вход символа 1 вызовет переход кодера в состояние 10, при этом в регистре будет храниться
последовательность 101, а выходные символы будут 1 0 1 =«n 2 = 0 и 1 1 =«n 2 = 0 .
Рассматриваемую диаграмму состояний можно развернуть во времени,
при этом будет получена так называемая кодовая решётка или решетчатая диаграмма (рис. 6.24б). Кодер имеет 2-разрядный сдвигающий регистр с четырьмя состояниями, следовательно, столбцы решётки содержат по четыре узла, помеченных содержимым регистра. Поэтому левый символ в обозначении узла равен последнему информационному символу, поступившему в регистр.
Порядок обозначения узлов выбран так, что при входящем символе 0 регистр переходит в следующее состояние по верхнему ребру (переходы отображены сплошной линией), а при 1 – по нижнему (переходы отображены пунктирной линией). Маркировка рёбер совпадает с комбинацией элементарного блока,
посылаемого в канал связи. По-прежнему информационной последовательности соответствуют путь на кодовой решётке и кодовое слово.
Если входные символы 01100, то по решётке находим кодовое слово 00 11 01 01 11. Таким образом, решётчатая диаграмма однозначно связывает
209

информационную последовательность, последовательность состояний кодера и последовательность символов на его выходе.
Удобным графическим аппаратом для исследования кодирования и декодирования свёрточных кодов является также кодовое дерево, строящееся на основании диаграммы состояния кодера. Коды, допускающие подобное представление с помощью кодового дерева, называются древовидными. На рис. 6.25 представлено кодовое дерево для рассмотренного выше несистематического свёрточного кода.
Рис. 6.25. Кодовое дерево несистематического свёрточного кода с порождающими |
|||
многочленами |
= |
1 + + > |
и M> = 1+> |
M |
210 |
|
|
