Методическое пособие Теория информации-2

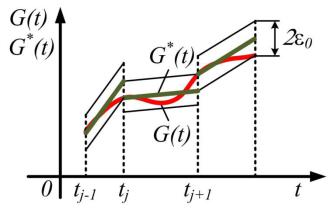
Проведем адаптивную дискретизацию реализации сигнала ‹( ),

изображенного на рис. 3.8, полиномом типаε (3.23) первой степени. Наибольшее допустимое отклонение примем равным #.

На момент i начала каждого интервала аппроксимирующий полином будет соответствовать многочлену:

	#			i	′	i	(3.26)
	где ‹′hij – производная сигнала ‹ в момент времени i.
	Момент очередного отсчёта определяется выполнением равенства:
	δÕ		i	′ i		#	(3.27)

Результаты дискретизации приведены на рис. 3.8.

Рис. 3.8. Адаптивная дискретизация сигнала с использованием степенного

многочлена первой степени

При аппаратной реализации данного алгоритма следует иметь в виду, что вследствие наличия операции дифференцирования сигнала он неэффективен при наличии высокочастотных помех.

3.5. Квантование сигналов

Мгновенное значение непрерывного сигнала ‹i представляет собой случайную величину. Диапазон её изменения, называемый непрерывной шкалой мгновенных значений сигнала, ограничен значениями ‹SI и ‹SÒÁ, что

71

отражает условие физической реализуемости сигнала. Непрерывную шкалу

мгновенных значений сигнала

разбивают на n интервалов,

называемых

шагами

квантования. Границами шагов квантования являются

‹ = ‹SÒÁ

− ‹SI

значения

′ ‹

= ‹ , ‹ , … , ‹

, ‹

= ‹

.

Из

множества

мгновенных

значений,

I’

I

‹

i– му’шагу квантованияSÒÁ

, только одно

принадлежащих# SI

значение

I является разрешенным (i– й уровень

квантования). Любое другое из

(‹

′

≤ ‹ < ‹ )

′

I

‹

значений

округляется

до .

Совокупность

величин

указанного множества

(i = 1, 2, ..., n) образует дискретную шкалу

уровней квантования. Если эта

I

‹

I’

I

′

′

′

постоянна на всём

шкала равномерна, т.е. разность значений ∆

протяжении

непрерывной шкалы

мгновенных

значений сигнала

′

i

,

‹ = ‹ − ‹

квантование

называют

равномерным. Если постоянство значений

не

∆‹h

j

выдерживается – квантование неравномерное. Благодаря простоте

технической

‹

реализации равномерное квантование получило наиболее широкое

распространение.

i

В

результате

замены

мгновенного

′

значения

сигнала

δ

= ‹h

j − ‹

′

I

погрешность

соответствующим

уровнем квантования

возникает

‹h j

Õ

i

, которую называют ошибкой

квантования.

Эта погрешность

‹

является

случайнойI

величиной.

Ошибку квантования характеризуют

двумя

величинами: максимальным значением и среднеквадратичным отклонением на всём диапазоне изменения мгновенных значений сигнала. Также применяют приведенные значения данных характеристик:

		δSÒÁ# = ‹SÒÁ − ‹SI					(3.29)
							(3.28)
		#	SÒÁ		SI
С целью	минимизации ‹			ошибки		квантования	непрерывную шкалу
					− ‹
‹	=
мгновенных значений сигнала целесообразно разбить на n одинаковых шагов
квантования ∆ ′		ÕÞßà’ÕÞT-	и	уровни		квантования	поместить в середине
					72

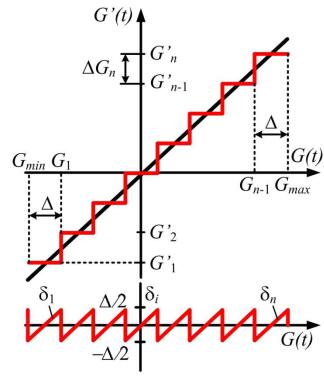
каждого шага (0рис.5 .‹3.9). При таком подходе максимальная ошибка квантования не превышает ∆ ′.

Рис. 3.9. Схема квантования сигнала и ошибка квантования сигнала

Если каждый уровень квантования выбран равным верхней или нижней

‹

′

I

границе шага квантования, то максимальное значение ошибки квантования

возрастает до ∆ ′.

Среднеквадратическое отклонение ошибки квантования для i–ro

шага

зависит не только от шага

и расположения в нем i–ro уровня

квантования,

σ

но и от закона

распределения мгновенных значений сигнала в пределах этого

Δ‹I

шага.

σ

=

â

I

• h‹ − ‹ j

<(‹)d‹

(3.30)

T

I′

В данном выражении

ÕT£'

– функция плотности вероятности мгновенных

значений сигнала G.

Считая шаги квантования малыми по сравнению с

<(‹)

<(‹)

диапазоном изменения сигнала,

плотность

в пределах каждого i– го шага

73

<можноh‹ j принять постоянной и равной некоторому среднему значению, например

σ I′ . При таких предположениях минимальная среднеквадратическая ошибка

I достигается при расположении уровня квантования в середине шага:

Δ‹Iã

ã

T

δ

ã

)Δ‹

ã

(3.31)

σ = â<(‹

) •

dδ = <(‹

12

I

I

’äÕTå⁄

I

I

Ú

I

I

′

′

Δ‹I′

(3.32)

δI = <h‹IjΔ‹I

12

Дисперсия полной ошибки квантования σ2 для всей непрерывной шкалы мгновенных значений сигнала определяется как математическое ожидание

дисперсий æÕT′( на отдельных шагах квантования:

σ = K σI		=			K <h‹I′jΔ‹I′	(3.33)
IQ				12 IQ
При равномерном квантовании выражение (3.33) примет вид:
σ =	Δ‹I′			K <h‹I′jΔ‹I′		(3.34)
12				IQ
Так как ∑IQ <h‹I′jΔ‹I′ = 1, то выражение (3.34) примет вид:
	σ		=		Δ‹I′	(3.35)
					12

Таким образом, при квантовании с постоянным шагом и размещении уровней квантования в середине шага (равномерное квантование)

среднеквадратическая ошибка квантования как для равномерного, так и для произвольного распределения мгновенных значений сигнала одинакова:

σ = 2√3	(3.36)
I′

При квантовании сигнала по уровню случайный процесс заменяется

74

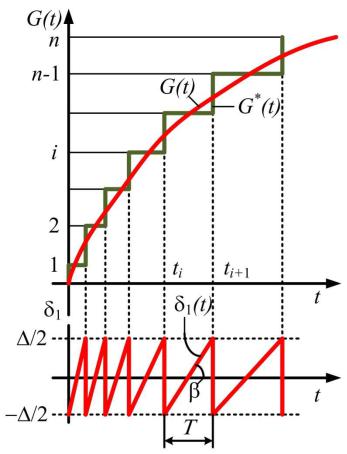
ступенчатой (зависимостью) ‹′( ). Изменяющуюся во времени ошибку квантования δ , также представляющую собой случайный процесс, называют шумом квантования:

		δ			′					(3.37)
При малом шаге квантования и допущении о равномерности
равномерного		‹( )		( )					при условии, что
распределения в нем мгновенных значений сигнала,
случайные процессы			и δ		эргодические, среднеквадратическую ошибку
	квантования σ			можно определить		через				(рис. 3.10). В
пределах каждого шага квантования ∆ зависимость									Iзаменяется прямой
								δ ( )
tgβI, где β – переменный угол наклона прямой.							δI( )

Рис. 3.10. Схема равномерного квантования и среднеквадратичная ошибка

При размещении уровней квантования в середине каждого шага

математическое ожидание ошибки квантования равно нулю, а её

75

среднеквадратическое значение определяется выражением:

σ = é1	$ë
	• ( ∙ tgβ) d	(3.38)

	’$ë
Так как tgβ =		σ = ä√ ,
	$∆, то значение среднеквадратичного отклонения

что соответствует ранее полученному (3.36).

При заданной допустимой среднеквадратической ошибке квантования и отсутствии помех число уровней квантования находим из соотношения:

2√3σ

(3.39)

При неравномерном законе распределения мгновенных значений сигнала квантование с постоянным шагом не является оптимальным по критерию минимума среднеквадратической ошибки σ. Квантуя участки с менее вероятными значениями сигнала с большим шагом, указанное значение среднеквадратической ошибки можно уменьшить. ‹( )

Докажем, что при<(‹)квантовании сигнала , имеющего плотность распределения значений , ‹(с постоянным) шагом ∆, значение которого много меньше диапазона изменения , среднеквадратическая ошибка квантования σ достигает минимума при расположении уровня квантования в середине шага.

Дисперсия ошибки квантования в пределах i-го шага в соответствии с

(2.38) может быть записана в виде:

σ = <h‹I′j	• h‹ − ‹I′j d‹ = <h‹I′j 1		ºh‹I − ‹I′j − h‹I’ − ‹I′j » ,	(3.40)
	ÕT£'	3

где ‹I′ – i-й уровень квантования.

Приравнивая нулю производную этого выражения, находим условие минимума дисперсии ошибки квантования:

76

		I = <h‹I′j ºh‹I − ‹I′j − h‹I’ − ‹I′j » = 0 ,				(3.41)
откуда	получаем равенство:
		Æ‹
		I	I′	I’	I′	(3.42)
При		одинаковых знаках		имеем ‹I	= ‹I’ , что соответствует	случаю

отсутствия квантования (∆ = 0). Приняв разные знаки, получаем выражение:

‹I′ =

T T£'

,

(3.43)

что и требовалось показать.

В реальных условиях на квантуемый сигнал всегда воздействует помеха.

Поэтому целесообразно минимальный шаг квантования выбирать с учётом вероятностных характеристик этой помехи.

Предположим, что помеха аддитивна. Тогда мгновенное значение сигнала

G, попадавшее ранее в i-й шаг квантования и сопоставлявшееся с уровнем квантования ‹I′, в результате действия помехи примет значение ‹ + ξ и может быть поставлено в соответствие другому уровню квантования ‹µ′ . Такой исход приведёт к искажению информации и вероятность его не должна превышать

допустимого значения.	вероятность сопоставления′
Обозначим через <I í условную′			значения
сигнала уровню квантования ‹µ вместо уровня ‹I		при условии, что		‹
<I H < 1.		помехи <I í > 0,
принадлежит i-му шагу квантования.	При наличии			а
Полная вероятность того, что величина ‹ + ξ останется в пределах i-го
шага квантования, может быть определена выражением:
T
<I = <I H ÕT•£' < ‹ d‹			(3.44)
Вероятность <I можно найти также, используя плотность вероятности
² ‹, ξ системы двух случайных величин	‹ и ξ:
77

<I = ï ²(‹, ξ) d‹ dξ ,	(3.45)
ð
где • – область интегрирования.

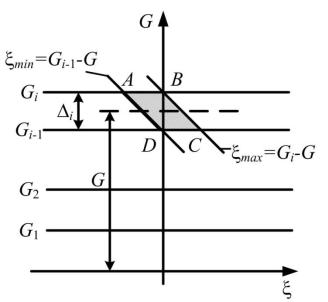
Поскольку учитываются мгновенные значения сигнала, принадлежащие i-му шагу квантования, границами интегрирования по ‹ являются значения ‹I и

‹I’ . Верхняя ξSÒÁ и нижняя ξSI границы интегрирования по ξ определяются

из следующего условия: алгебраическая сумма сигнала и помехи не должны выйти за пределы i-го шага квантования:

SÒÁ		I	(3.46)
SI		I’	(3.47)
Отсюда получаем выражения:	I
SÒÁ			(3.48)
SI	I’		(3.49)

Область интегрирования представлена на рис. 3.11 в виде параллелограмма ABCD.

Рис. 3.11. Область интегрирования для уравнения (3.45)

Пусть помеха некоррелированна с сигналом, тогда справедливо

78

выражение:

<I(H) =	ÕT£'	ñÞT-			,	(3.50)
		¶ÕÕTT£' <(‹) d‹
где < ξ – плотность распределения помехи.
Далее будем рассматривать только случай равномерного квантования
сигнала, мгновенные значения которого в диапазоне от						‹SI до ‹SÒÁ
распределены равномерно:
< ‹ = SÒÁ			SI			(3.51)
Сделаем допущение о равномерном‹ − ‹				распределении значений помех. В

этом случае:

< ξ = , ,	(3.52)
где Ò – амплитуда помехи, симметричной относительно мгновенного значения

сигнала.

При указанных условиях результаты расчета инвариантны относительно

шага квантования и зависят только от соотношения , и = I. Определим <I H

при , < . Область интегрирования представлена на рис. 3.12.

Рис. 3.12. Разбиение области интегрирования для расчёта уравнения (3.50)

В соответствии с разбиением преобразуем выражение (3.50) с учетом того, что знаменатель данного выражения равен ∆/ ‹SÒÁ − ‹SI , к

следующему виду:

79

<I(H) = • 1 •

1 dξ d‹ = • 1 • 1 dξ d‹ +

(3.51)

∆

ñÞT-

,

# ∆

’Ò ,

∆

#

∆

∆

’Ò⁄

1

Ò⁄

1 dξ d‹ + ∆

•

1

’Õ

1 dξ d‹ = 1 −

,

+ •

•

•

Ò⁄

∆

’Ò⁄

,

’Ò⁄

∆

’Ò⁄

,

4

∆

<I(H) = 1 − ;Ò∆

< (H)

, ≥ 2Δ

и <I(H) = Ò,

< , ≤ 2Δ

∆

I

при условиях, что

и

:

Аналогично определим

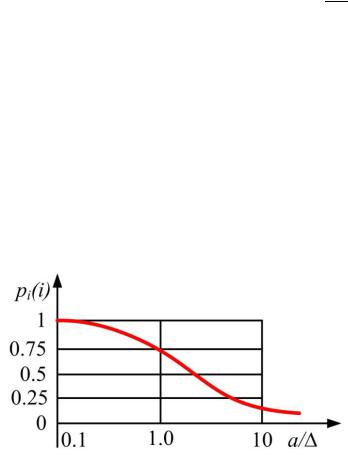
соответственно. На рис. 3.13 представлен график

<I(H) = ² @Ò∆A из

которого,

в частности, следует, что

нецелесообразно

выбирать меньше ,

поскольку

при

Ò

резко возрастает вероятность

неправильного

квантования сигнала.

∆ > 1

,

Рис. 3.13. Распределение вероятности сопоставления значения сигнала с уровнем

′

случая воздействия на сигнал равномерно

квантования ‹I

дляраспределённой помехи

ô

I

(рис. 3.14)

Аналогично рассчитывают зависимость

п

для

∆

случая воздействия на сигнал помехи,

распределенной по нормальному закону:

`’õ(

<

(H) = ² @ A

<(ξ) =

п

(3.52)

σ

п

ξ

п – среднеквадратическое

отклонение помехи .

где

σ √2

80