Методическое пособие Теория информации-2

&	энтропия	= 2 O	(2.47)
	единица времени

При рассмотрении непрерывных сигналов иногда требуется перейти из одной системы координат в другую. Рассмотрим кратко преобразование кратных интегралов при переходе к новой системе координат. Пусть дан интеграл следующего вида:

					• • • ² °, ´, d° d´ d
°, ´,	Требуется	перейти			к новым				координатам g, R, ω, причем		координаты
	являются функциями от g, R, ω:										(2.48)
	Элементарный объём, после преобразования к новым переменным будет
определяться выражением:
		Æg	ÆR		Æω	ÅÅ				°, ´,
	d° d´ d =	ÅÅÆ´	Æ´		Æ´						(2.49)
		Æg	ÆR		Æω	ÅÅ		dg dR dω = ¹Ç cg, R, ωd¹ dg dR d”
		ÅÅÆ	Æ		Æ
		Æg	ÆR		Æω
°, ´,	Величина Ç @s,t,•Á,È,ž A				называется якобианом преобразования от координат
	к координатам g, R, ω и характеризует соотношение масштабов старых и
новых систем координат. Важным свойством якобиана является равенство:
			¹Ç c	g, R, ω			d¹ =		g, R, ω	A¹	(2.50)
									¹Ç @°, ´,
	Тогда после преобразования интеграл будет выглядеть следующим
образом:		d° d´ d			= • • • Ä g, R, ω ¹Ç cg, R, ωd¹ dg dR dω
• • • ² °, ´,											(2.51)
									51

Исходя из вышесказанного распределения вероятности – важной Функция распределения вероятностей удовлетворяет условию:

рассмотрим преобразование функции

<характеристики(° , ° , … , ° ) непрерывного сигнала.

всегда нормирована, т.е.

				(2.52)

где интегрирование производится по всем возможным значениям переменных

	.	переменные					заменяются на новые:			.
Пусть
° , ° , … , °
			распределения вероятностей в новых координатах,
Определим		функцию		° , ° , … , °					´ , ´ , … , ´
обозначив её J(´ , ´ , … , ´ ). По условию нормировки можно записать:
									(2.53)

Тогда, введя в уравнении (2.52) новое значение для элементарного объёма, выраженное в соответствии с (2.49), и приравняв к уравнению (2.53),

получим:

´ , ´ , … , ´		(2.54)
• … • J(´ , ´ , … , ´ ) d´ d´ … d´

Из уравнения (2.54) следует, что функция распределения вероятностей в новых координатах:

(2.55)

Выражение

(2.55)

является

формулой для преобразования функции

´ , ´ , … , ´

распределения вероятностей из одной системы координат в другую.

Рассмотрим, как меняется

энтропия

распределения вероятностей

при

преобразовании

координат

° , ° , … , °

°

´ , ´ , … , ´

.

´

в координаты

´ , ´ , …–

Для

сокращения записи обозначим° , ° , … , °

через

, а

, ´через

.

52

Тогда энтропия в данных системах координат может быть определена уравнениями:

Подставив в уравнение (2.57) выражения для J(´) и

уравнениями (2.49) и (2.50), получим выражение:

°	° ´	´	´ °	°
= − • Ç c´d <(°) log Ç c´d Ç @°A d° − • Ç c´d <(°) log <(°)
		°
= − • <(°) log Ç c´d d° − • <(°) log <(°) d° =
		°
	= − • <(°) log Ç c´d d° + O(°)
Величина	− ¶ <(°) log ºÇ @ÈÁA» d°		в правой	части

(2.56)

(2.57)

d´ в соответствии с

Ç @´°A d° =

(2.58)

выражения (2.58)

представляет собой математическое ожидание (среднее значение) логарифма якобиана преобразования от старых координат к новым. Таким образом,

энтропия при переходе к новым координатам равна энтропии распределения вероятностей при первичной системе координат за вычетом математического ожидания логарифма якобиана преобразования от старых координат к новым.

Рассмотрим изменение энтропии при линейном преобразовании координат в соответствии с формулами:

´ = , ° + , …° + + , °

´ = , ° + , ° + + , °

(2.59)

Якобианы такого преобразования будут иметь вид:

53

Ç @´A = ÅÆ´° ° Æ°… ÅÆ´ Æ°

Æ´° … Æ´° Å

Æ°… … Æ°… Æ´ … Æ´ Å Æ° … Æ°

= Å, ,

,… ,…

…		1
	,
…	…	Å = Ç @°A
…		´
	,

Записывая определитель матрицы коэффициентов преобразования сокращённо, получим выражение:

´Ii

(2.60)

линейного

(2.61)

Следовательно, выражение для энтропии при линейном преобразовании координат примет вид:

= O(°) − logÉ,IiÉ’ • <(°) d° = O(°) + logÉ,IiÉ	(2.62)
´

Стоит отметить, что если при преобразовании координат не происходит изменения масштаба, напримерÇ = 1, при повороте координатной системы или при смещенииO(´) = O(°её) начала, и, следовательно, энтропия не меняется:

.

во втором –	.		<(° , ° , … , ° )
Рассмотрим энтропию двух независимых ансамблей функций. Пусть
функция распределения вероятностей в первом ансамбле есть			, а
При	линейной суперпозиции (рис.	2.6) функция распределения
	J(° , ° , … , ° )

вероятностей в ансамбле сумм имеет вид:

											(2.63)
		’È(
Предположим∙ Jh°	,− что´ , ° средние, … , ° максимальные− ´ j d´ d´								…квадратичныеd´		значения в
исходных ансамблях равны,			соответственно,			5	и	5		, а энтропийные мощности
					54

этих ансамблей – 5Ë и 5Ë .

Рис. 2.6. Линейная суперпозиция ансамбля сумм

Среднее максимальное5Ë квадратичное значение суммы будет 5 , а её энтропийная мощность – . Тогда, при эргодичности и независимости исходных ансамблей справедливы соотношения (2.64) и (2.65):

(2.64)

(2.65)

Равенство (2.64) соответствует утверждению, что при линейном сложении двух некогерентных эргодических ансамблей их среднее максимальное квадратичное значение обладает свойством аддитивности.

Неравенство говорит о том, что при сложении двух некогерентных эргодических ансамблей энтропия на единицу среднего максимального квадратичного значения возрастает или, в крайнем случае, не убывает. Это означает, что в суммарном ансамбле по сравнению с исходными ансамблями связи между символами будут слабее, поскольку, если исходные ансамбли некогерентны, то имеющиеся в них связи не могут быть согласованы друг с другим и, следовательно, при сложении ансамблей эти связи ослабляются.

Кроме того, распределение вероятностей в точках отсчёта в суммарном ансамбле будут стремиться к нормальному. Можно заключить, что при

55

сложении двух некогерентных эргодических ансамблей суммарный ансамбль будет ближе к ансамблю случайных шумов, который характеризуется максимально возможной средней энтропией на величину максимального квадратичного значения.

56

3. Преобразование непрерывных сигналов в дискретные

Хотя поступающую информацию можно хранить, передавать и обрабатывать как в виде непрерывных, так и в виде дискретных сигналов, на современном этапе развития информационной техники предпочтение отдаётся дискретным сигналам. С этой целью каждый непрерывный сигнал подвергается операциям квантования по времени (дискретизации) и по уровню.

Под дискретизацией подразумевают преобразование функции непрерывного времени в функцию дискретного времени, представляемую совокупностью величин, называемых координатами, по значениям которых исходная непрерывная функция может быть восстановлена с заданной точностью.

Под квантованием подразумевают преобразование некоторой величины с непрерывной шкалой значений в величину, имеющую дискретную шкалу значений. Оно сводится к замене любого мгновенного значения одним из конечного множества разрешённых значений, называемых уровнями квантования.

3.1. Общая постановка задачи дискретизации непрерывного сигнала

записано в виде:

(Ì , Ì , … , Ì=)

на

В самом общем случае представление непрерывного сигнала

интервале

времени

совокупностью

значений

может

быть

‹( )

!

=

,

(3.1)

где

–

оператор

дискретного представления сигнала, реализуемый

устройством, называемым дискретизатором.

Аналогично можно

записать

и операцию

восстановления

по

совокупности координат

непрерывной

функции в

виде

δ( ) = ‹( ) − ‹ ( )

воспроизводящей функции

(Ì

, Ì,

, … , Ì

)

текущей погрешностью

приближения

:

‹ ( )

57

						= ,			(3.2)
где		– оператор	восстановления	сигнала,			реализуемый		соответствующим
устройством.
	‚
	С точки зрения математики задача дискретизации сводится к
совместному выбору пары операторов						и	‚	, а также к выбору критериев
оценки		точности	восстановления	сигнала.				Широкое применение нашли
					!

линейные операторы. В этом случае для определения координат сигнала используется следующее соотношение:

			Ìi = • ξi( )‹( ) d = !‹( ),			(3.3)
	ξ ( )		m = 1,2, … , 5	$
						аппроксимирующим
где	i	для		– система весовых функций.
	Воспроизводящая			функция	представляется
полиномом:			‹ ( ) = K Ìi( )φi( ) = ‚ Ì , Ì , … , Ì= ,
						(3.4)
			iQ
где φi для m = 1,2 … 5 –				система базисных функций.
	При одном и том же операторе дискретного представления сигнала ! для

восстановления могут использоваться различные операторы восстановления сигнала ‚. Методы дискретизации в первую очередь разделяются в зависимости от способа получения координат сигнала.

В случае, когда в качестве весовых функций используются базисные функции, т.е. в случае когда ξi = φi , координаты Ì , Ì , … , Ì= сигнала

‹ получаются «взвешенным» интегрированием сигнала на некотором

интервале времени Т. При этом предполагается, что базисные функции ортогональны и обеспечивают сходимость к ‹ при N → ∞ , что даёт возможность ограничить число координат в соответствии с заданной погрешностью восстановления.

58

Предъявляя дополнительные требования к базисным функциям, можно

провести дискретизацию различных моделей сигнала.

	, взятых в		‹( )
	Широкое распространение получили методы дискретизации, при которых
‹h j									(m = 1,2 … 5)
непрерывный сигнал						заменяется совокупностью его мгновенных значений
i		определённые моменты времени						i	, и называемых
выборками или отсчётами.						i i’
	Отрезок времени ∆						между соседними выборками называют
шагом дискретизации.				Если он выдерживается постоянным во всем диапазоне
					= −

преобразования сигнала, дискретизация считается равномерной. Методы равномерной дискретизации получили наиболее широкое применение. Они характеризуются простым алгоритмом, исключающим необходимость фиксировать время отсчётов, что существенно облегчает техническую реализацию. Если отрезки времени между выборками меняются, например, в

зависимости от скорости изменения сигнала или по заданной программе,

дискретизацию называют неравномерной.

В теоретических исследованиях наибольшее распространение получила модель сигнала в виде квазистационарного случайного процесса, каждая реализация которого представляет собой функцию с ограниченным спектром.

Величина шага дискретизации в этом случае ставится в зависимость от наивысшей частоты спектра. Такой критерий выбора отсчётов принято называть частотным.

3.2. Равномерная дискретизация Ðс использованием модели сигнала со спектром, ограниченным частотой

Правило выбора предельного шага при равномерной дискретизации с использованием модели сигнала с ограниченным спектром – теорема Котельникова – было подробно рассмотрено в разделе 2. Поэтому рассмотрим только некоторые аспекты применения данной теоремы.

Процедура теоретического восстановления в этом случае конкретной

59

функции ‹( ), принадлежащей некоторому ансамблю функций, по её отсчётам

сводится к следующему. На передающей стороне в исходной непрерывной

функции

через интервалы времени ∆

связи

определяются мгновенные

значения ‹( ) ∆

и

передаются в

канал

в виде δ– импульсов с

=

−

‹(

)

и бесконечно малой длительностью

, имеющих площади

,

амплитудами

равные

‹( )

3.1а– б). На приёмной стороне

τтакая

последовательность

∆

!

(рис.

! τ

импульсов пропускается через идеальный фильтр нижних частот, у которого

			‹( )
частота среза равна		ф. При длительной передаче сигнал на выходе фильтра
будет	воспроизводить переданный непрерывный сигнал			(рис. 3.1в).

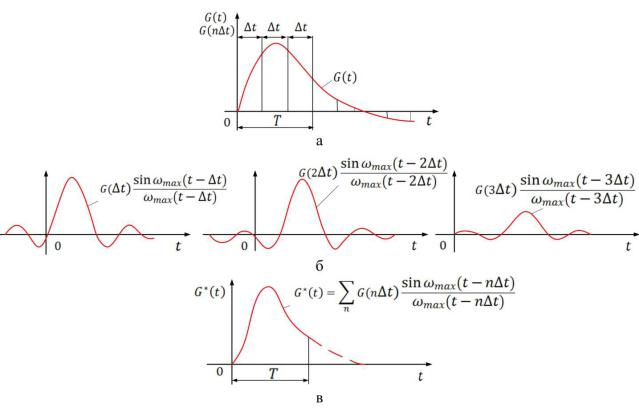
Рис. 3.1. Схематичное представление равномерной дискритезации в соответствии с теоремой Котельникова и востановления непрерывного сигнала: а – исходный непрерывный сигнал; б – значения функции в точках отсчёта;

в – востановленный сигнал

При реализации такой системы дискретизации на практике происходит

искажение сигнала. Реальный сигнал имеет конечную длительность Т и,

60