Методическое пособие Теория информации-2

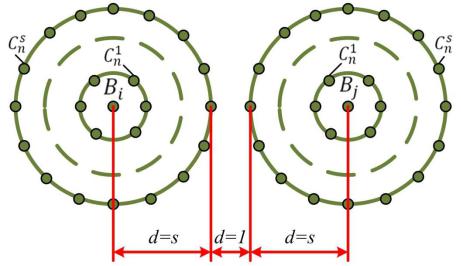
В общем случае для обеспечения возможности исправления всех ошибок кратности до x включительно при декодировании каждая из ошибок должна приводить к запрещённой комбинации, относящейся к подмножеству исходной разрешённой кодовой комбинации (рис. 6.6).

Подмножество каждой из разрешённых n-разрядных комбинаций y (рис. 6.6) складывается из запрещённых комбинаций, являющихся следствием

∙единичных ошибок (они располагаются на сфере радиусом n = 1, и их число равно J );

∙двойных ошибок (они располагаются на сфере радиусом n = 2, и их число равно J>) и т.д.воздействия:

Рис. 6.6. Подмножество разрешённых комбинаций для обеспечения возможности исправления всех ошибок кратности до x включительно

Внешняя сфера подмножества имеет радиус n = x и содержит Jz

запрещённых кодовых комбинаций.

Поскольку указанные подмножества не должны пересекаться,

минимальное кодовое расстояние между разрешёнными комбинациями должно удовлетворять соотношению (6.6).

161

%		(6.6)
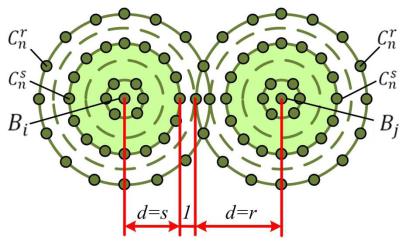
Нетрудно убедиться в том, что для исправления всех ошибок кратности x
и одновременного обнаружения всех ошибок кратности	]	при условии, что

] ≥ x, минимальное кодовое расстояние (рис. 6.7) нужно выбирать из условия:

%	(6.7)

Формулы, выведенные для случая взаимно независимых ошибок, дают завышенные значения минимального кодового расстояния при помехе,

коррелированной с сигналом.

Рис. 6.7. Подмножество разрешённых комбинаций для обеспечения возможности исправления кодом всех ошибок кратности x и одновременного обнаружения всех ошибок кратности ]

В реальных каналах связи длительность импульсов помехи часто превышает длительность символа, что приводит к искажению нескольких расположенных рядом символов комбинации, т.е. к появлению пакетов ошибок.

Длиной пакета ошибок называют число следующих друг за другом символов,

начиная с первого искажённого символа и кончая искажённым символом, за которым следует не менее | неискажённых символов. Основой для выбора |

служат статистические данные об ошибках. Если, например, кодовая комбинация 00000000000000000 трансформировалась в комбинацию

01001000010101000 и | принято равным трём, то в комбинации имеется два

162

пакета длиной 4 и 5 символов (пакеты ошибок выделены жирным начертанием).

Для пакета ошибок при той же корректирующей способности минимальное кодовое расстояние между разрешёнными комбинациями может

быть меньше.

Отметим, что каждый конкретный корректирующий код не гарантирует исправления любой комбинации ошибок. Корректирующие коды предназначены для исправления комбинаций ошибок, наиболее вероятных для

заданного канала связи и наиболее опасных по последствиям.

Если характер и уровень помехи отличаются от предполагаемых,

эффективность применения корректирующего кода резко снизится.

Применение корректирующего кода не может гарантировать безошибочного приёма сообщения, но даёт возможность повысить вероятность получения на

выходе правильного результата.

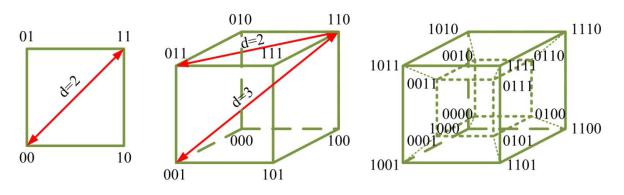
Любая n-разрядная двоичная кодовая комбинация может быть интерпретирована как вершина n-мерного единичного куба, т.е. куба с длиной

ребра, равной 1.
При N = 2 кодовые комбинации располагаются в вершинах квадрата
(рис.	6.8); при	N = 3	–	в вершинах единичного куба; при
N = 4 –	в вершинах четырёхмерного куба.

Рис. 6.8. Геометрическая интерпретация блоковых корректирующих кодов

В общем случае n-мерный единичный куб имеет 2 вершин, что равно

163

и центром в вершине, соответствующей данной разрешенной кодовой

наибольшему возможному числу кодовых комбинаций. Кодовое расстояние между отдельными кодовыми комбинациями соответствует наименьшему числу ребер единичного куба, которые необходимо пройти, чтобы попасть от одной комбинации к другой.

Теперь метод декодирования при исправлении одиночных независимых ошибок можно пояснить следующим образом. В подмножество каждой

разрешённой} комбинации относят все вершины, лежащие в сфере с радиусом

B )

>

комбинации. Если в результате действия шума комбинация переходит в точку,

находящуюся внутри сферы } >B ), то такая ошибка может быть исправлена.

Если помеха}смещает точку разрешённой комбинации на границу двух сфер (расстояние >) или дальше (но не в точку, соответствующую другой

разрешённой комбинации), то такое искажение может быть обнаружено. В

условиях независимого искажения символов лучшие корректирующие коды – это такие, у которых точки, соответствующие разрешённым кодовым комбинациям, расположены в пространстве равномерно.

Одной из основных характеристик корректирующего кода является избыточность кода, указывающая степень удлинения кодовой комбинации для достижения определённой корректирующей способности. Если на каждые N

символов выходной последовательности, поступающей из кодера в канал связи приходится P информационных и N − P проверочных символов, то относительная избыточность кода может быть выражена одним из соотношений:

? =	N	(6.8)
? =	P	(6.9)

Величина ? изменяется от 0 до ∞ и характеризует избыточность кода.

164

Коды, обеспечивающие заданную корректирующую способность при минимально возможной избыточности, называют оптимальными.

В связи с нахождением оптимальных кодов оценим, например,

наибольшее возможное число Q разрешённых комбинаций n-значного

двоичного кода, обладающего способностью исправлять взаимно независимые
ошибки кратности до x включительно. Это равносильно отысканию числа
комбинаций, кодовое расстояние между которыми не менее, чем				= 2x + 1.
Общее число различных исправляемых ошибок для		каждой разрешённой
			n
комбинации составляет ∑z	J . Каждая из таких ошибок должна приводить к

запрещённой комбинации, относящейся к подмножеству данной разрешённой

комбинации. Совместно с этой разрешённой комбинацией подмножество
включает	~1 + ∑z	J • комбинаций.
Как	отмечалось, однозначное декодирование возможно только в том

случае, когда названные подмножества не пересекаются. Так как общее число

различных комбинаций n-значного двоичного кода составляет

2 , число

разрешённых

комбинаций

€

не может превышать

>•

, т.е.

получаем

i∑ƒ„U ‚•

верхнюю оценку Хэмминга:

€ ≤ 1 + ∑z

J

(6.10)

В табл. 6.9 приведены значения кодового расстояния n и

соответствующие им значения €.

Таблица 6.9

Значения … для разных кодовых расстояний †

1

2

3

≤ N + 1

5

≤ N> + N + 2

2

≤ 2B

4

≤

N

2P + 1

≤ 1 + J + J> + + JQ

Коды,

для которых

в

приведенном

соотношении для

€ достигается

165

равенство, называют также плотноупакованными.

Однако не всегда целесообразно стремиться к использованию кодов,

близких к оптимальным. Необходимо учитывать другой, не менее важный показатель качества корректирующего кода – сложность технической реализации процессов кодирования и декодирования.

Если информация должна передаваться по медленно действующей,

ненадёжной и дорогостоящей линии связи, а кодирующее и декодирующее устройства предполагается выполнить на высоконадёжных и быстродействующих элементах, то сложность этих устройств не играет существенной роли. Решающим фактором в таком случае является повышение эффективности использования линии связи и поэтому желательно применение корректирующих кодов с минимальной избыточностью.

Если же корректирующий код должен быть применён в системе,

выполненной на элементах, надёжность и быстродействие которых равны или близки надёжности и быстродействию элементов кодирующей и декодирующей аппаратуры (например, для повышения достоверности воспроизведения информации с запоминающего устройства цифровой вычислительной машины), то критерием качества корректирующего кода является надёжность системы в целом, т.е. с учётом возможных искажений и отказов в устройствах кодирования и декодирования. В этом случае часто более целесообразны коды с большей избыточностью, но обладающие преимуществом простоты технической реализации.

Наиболее часто применяются блоковые коды. При использовании блоковых кодов цифровая информация передаётся в виде отдельных кодовых комбинаций (блоков) равной длины. Кодирование и декодирование каждого блока осуществляется независимо друг от друга, то есть каждой последовательности символов сообщения = соответствует блок из N символов.

Самый большой класс разделимых кодов составляют линейные коды, у

которых значения проверочных символов определяются в результате

166

проведения линейных операций над определенными информационными символами.

Линейные коды

Для случая двоичных кодов каждый проверочный символ выбирают таким, чтобы его сумма с определёнными информационными символами была равна нулю. Символ проверочной позиции имеет значение 1, если число единиц информационных разрядов, входящих в данное проверочное равенство,

нечётно, и 0, если оно чётно. Число проверочных равенств (а следовательно, и

число проверочных символов) и номера конкретных информационных разрядов, входящих в каждое из равенств, определяются тем, какие и сколько ошибок должен исправлять или обнаруживать данный код. Проверочные символы могут располагаться на любом месте кодовой комбинации.

При декодировании определяется справедливость проверочных равенств.

В случае двоичных кодов такое определение сводится к проверкам на чётность числа единиц среди символов, входящих в каждое из равенств (включая проверочный). Совокупность проверок даёт информацию о том, имеется ли ошибка, а в случае необходимости и о том, на каких позициях символы искажены.

Любой двоичный линейный код является групповым, так как совокупность входящих в него кодовых комбинаций образует группу.

Систематическими кодами называются блочные N, P коды, у которых P

разрядов (обычно первые) представляют собой двоичный неизбыточный код, а

последующие N − P – контрольные разряды сформированы путём линейных преобразований над информационными.

Построение конкретного корректирующего кода производят исходя из требуемого объёма кода €, т.е. необходимого числа передаваемых команд или дискретных значений измеряемой величины и статистических данных о наиболее вероятных векторах ошибок в используемом канале связи. Вектором ошибки называют n-разрядную двоичную последовательность, имеющую

167

единицы в разрядах, подвергшихся искажению, и нули во всех остальных разрядах. Любую искажённую кодовую комбинацию можно рассматривать теперь как сумму (или разность) по модулю 2 исходной разрешенной кодовой комбинации и вектора ошибки.

Исходя из неравенства 2Q − 1 ≥ € (нулевая комбинация часто не

используется, так как не меняет состояния канала связи) определяем число
информационных P разрядов, необходимое для передачи заданного числа
команд обычным двоичным кодом.
Каждой из 2Q − 1 ненулевых комбинаций -разрядного безызбыточного
кода нам необходимо поставить в соответствие комбинацию из		N символов.
Значения символов в N − P	проверочных разрядах такой	комбинации

устанавливаются в результате суммирования по модулю 2 значений символов в определённых информационных разрядах.

Поскольку множество 2Q комбинаций информационных символов

(включая нулевую) образует подгруппу группы всех -разрядных комбинаций,

то и множество 2Q N-разрядных комбинаций, полученных по указанному правилу, тоже является подгруппой группы N-разрядных кодовых комбинаций.

Это множество разрешённых кодовых комбинаций и будет групповым кодом.

Для построения корректирующего кода надлежит определить число проверочных разрядов и номера информационных разрядов, входящих в

каждое из равенств для определения символов в проверочных разрядах.

Разложим группу 2 всех -разрядных комбинаций на смежные классы по подгруппе 2Q разрешённых N-разрядных кодовых комбинаций, проверочные

разряды в которых ещё не заполнены. Помимо самой подгруппы кода в
разложении насчитывается 2 BQ − 1	смежных классов. Элементы каждого

класса представляют собой суммы по модулю 2 комбинаций кода и образующих элементов данного класса. Если за образующие элементы каждого класса принять те наиболее вероятные для заданного канала связи вектора ошибок, которые должны быть исправлены, то в каждом смежном классе

168

сгруппируются кодовые комбинации, получающиеся в результате воздействия на все разрешённые комбинации определённого вектора ошибки. Для исправления любой полученной на выходе канала связи кодовой комбинации теперь достаточно определить, к какому классу смежности относится комбинация. Складывая её затем (по модулю 2) с образующим элементом этого смежного класса, получаем истинную комбинацию кода.

Ясно, что из общего числа 2 − 1 возможных ошибок групповой код может исправить всего 2BQ − 1 разновидностей ошибок по числу смежных классов.

Чтобы иметь возможность получить информацию о том, к какому смежному классу относится полученная комбинация, каждому смежному классу должна быть поставлена в соответствие некоторая контрольная последовательность символов, называемая опознавателем (синдромом).

Каждый символ опознавателя определяют на приёмной стороне в результате проверки справедливости одного из равенств, которые составляют для определения значений проверочных символов при кодировании.

Ранее указывалось, что в двоичном линейном коде значения проверочных символов подбирают так, чтобы сумма по модулю 2 всех символов (включая проверочный), входящих в каждое из равенств, равнялась нулю. В таком случае число единиц среди этих символов чётное. Поэтому операции определения символов опознавателя называют проверками на чётность. При отсутствии ошибок в результате всех проверок на чётность образуется опознаватель,

состоящий из одних нулей. Если проверочное равенство не удовлетворяется, то в соответствующем разряде опознавателя появляется единица:

…0 …0… …0… … … …1… …0 0 1 0 0 0 (6.11)

1 0 0 0 0

Исправление ошибок возможно лишь при наличии взаимно однозначного соответствия между множеством опознавателей и множеством смежных

169

классов, а следовательно, и множеством подлежащих исправлению векторов ошибок.

Таким образом, количество подлежащих исправлению ошибок является определяющим для выбора числа избыточных символов N − P . Их должно быть достаточно для того, чтобы обеспечить необходимое число опознавателей

(синдромов).

Если, например, необходимо исправить все одинарные независимые ошибки, то исправлению подлежат N ошибок. Различных ненулевых опознавателей должно быть не менее N. Необходимое число проверочных разрядов, следовательно, должно определяться одним из соотношений:

(6.12)

	(6.13)

Если необходимо исправить не только все одинарные, но и все двойные независимые ошибки, соответствующее неравенство принимает вид неравенства:

		(6.14)

Вобщем случае для исправления всех независимых ошибок кратности до x включительно получаем:

			(6.15)

Стоит подчеркнуть, что в приведенных соотношениях указывается теоретический предел минимально возможного числа проверочных символов,

который далеко не во всех случаях можно реализовать практически. Часто проверочных символов требуется больше, чем следует из соответствующего равенства. Одна из причин этого выяснится при рассмотрении процесса

сопоставления каждой подлежащей исправлению ошибки с её опознавателем.

Проведём составление таблицы опознавателей для случая исправления одиночных ошибок. Допустим, что необходимо закодировать 15 команд. Тогда

требуемое число информационных	разрядов равно	четырём	log> 15 3.9	.
	170