Методическое пособие Теория информации-2

средняя информация = O m − OI m = 1 − 0.081 = 0.919 дв. ед.⁄символ.

символ

Полученное значение совпадает с предыдущим. Если процент ошибок возрастает⁄ с 1 до 50 %, то значение O m не меняется, а OI m возрастает до

1 дв. ед. символ. В этом случае количество передаваемой информации оказывается равным нулю. Если процент ошибок возрастает до 100 %, то передаваемая⁄ информация, как и в отсутствии шумов, оказывается равной

1.0 дв. ед. символ. Такой вывод совершенно понятен, так как передаваться может один из двух символов, и если известно, что он всегда передается неверно, то по принятому символу можно вполне достоверно установить переданный.

Ещё раз подчеркнем, что шум уменьшает количество содержащейся в сообщениях информации. Если некоторое сообщение, являющееся шумом,

уменьшает сведения о той или иной ситуации по сравнению с тем, что было известно до приёма сообщения, то оно содержит отрицательную информацию.

Надёжность каналов передачи информации и вопросы подавления шумов будут рассмотрены в 4 разделе данного пособия.

31

2. Непрерывная информация

2.1. Математическое определение непрерывной информации. Теорема

отсчётов во временном представлении

Во многих системах связи сигналы представляют собой не последовательность дискретных символов, а непрерывные функции от времени,

содержащие бесконечное множество точек (спектр). Значения непрерывных сигналов меняются постепенно и, следовательно, значение сигнала в данной точке всегда можно с большей или меньшей степенью точности предсказать по его значениям в предыдущих точках. Интервал времени между независящими друг от друга значениями непрерывного сигнала определяется полосой частот

сигнала.

Теорема отсчётов во временном представлении, называемая также

теоремой Котельникова, формулирует данное свойство непрерывных сигналов следующим образом. Рассмотрим непрерывный сигнал, прошедший через

систему с ограниченной полосой частот и описываемый функцией					. Тогда,
если функция			не содержит составляющих с частотой выше	W Гц, то она
					‹( )
полностью	определяется последовательностью её значений в точках, отстоящих
		‹( )
на расстоянии Œ секунд друг от друга.

Данная теорема формулирует тот факт, что не существует независимых значений непрерывного сигнала, отделённых друг от друга в среднем интервалами времени, меньшими, чем Œ. Таким образом, если ширина полосы

частот велика, то интервал между независящими друг от друга значениями сигнала мал. Напротив, если полоса частот узка, то этот интервал велик.

Приведём доказательство данной теоремы и определим условия, при

которых она выполняется. Пусть Ω					есть спектр функции	, который
	‹( )		комплексную функцию. Тогда непрерывная
может быть		выражен через		(ω)		‹( )
функция		в соответствии с обратным преобразованием Фурье может быть
определена следующим образом:
				32

	‹( ) = 2π			∞		(ω)`	I•&
				’•	Ω			‘ω			(2.1)
				∞
	Если вне диапазона частот выполняется условие Ω(ω) = 0, то:
	‹( ) =			• Ω(ω)`I•&‘ω							(2.2)
		2π ’ “Œ									, где
	Рассмотрим значения времени , удовлетворяющие условию
	– положительные или		отрицательные целые числа. Для						этих		моментов
										= Œ
времени выражение (2.2) примет вид:
	‹ @2 A = 2π			•		Ω(ω)`I• Œ‘ω					(2.3)

(ω)Разложим спектр функции в ряд Фурье на интервале −2π ≤ ” ≤ 2π .

Ω– обычно комплексная функция и в общем виде может быть определена’ “Œ

как:

Ω

,

где ,(ω), N(”)∞– вещественные функции.

I• “

1

∞

’I•;“Œ

!

, ω `

;“Œ

‘ω

,(ω) = K ! `

= 4π ’ •“Œ

Q’

’I• “

• N(ω)`

∞

;“Œ

‚

=

I•;“Œ

‘ω

N ω = K ‚ `

Q’

4π ’ “Œ

∞

Следовательно, можно записать:

∞

(! − H‚ )`

’I•;“Œ

∞

’I•;“Œ

,

Ω

∞

∞

(ω) = ,(ω) − HN(ω) = K

= K • `

•̅

Q’

Q’

где

– коэффициент комплексного ряда Фурье:

(2.4)

(2.5)

(2.6)

(2.7)

33

• = ! − H‚ = 4π ’ •“Œ a,(ω) − HN(ω)b`I•;“Œ‘ω =					(2.8)
=	1	“Œ	Ω	“
		•		(ω)`I•;“Œ‘ω
	4π ’ “Œ

Сопоставив выражения (2.3) и (2.8), можно записать, что:

Тогда

2

(2.9)

‹ @

A

• =

‹ @

A

(ω)

(2.10)

очередь,

заданном отрезке

совокупность

Таким образом, на

2

2

значений

полностью определяет

функцию

Ω

,

которая,

в свою

−2π ≤ ω ≤ 2π

однозначноŒ

определяет функцию

. Итак, существует одна и только

одна функция

со

спектром,

ограниченным частотой

,

которая в

точках

‹( )

отсчёта, отстоящих друг от друга на

принимает

наперёд заданные значения.

Теорема доказана.

Œ

Найдём аналитическое выражение для функции, заданной её значениями

в точках отсчёта. Для этого подставим (2.10) в (2.7):

∞

’I•Œ

Ω

∞

(2.11)

(ω) = 2 KQ’

‹ @2A `

Подставив (2.11) в (2.2), получим:

’I•

I•&

‹( ) =

•

‹ @

A `

˜ `

‘ω =

∞

Œ

(2.12)

2π

’ “Œ 2 ∞ Q’

2

∞

=

1

“Œ

K ‹

@

A

`

‘ω =

•

I•@&’ ŒA

Q’

∞

4π ’ “Œ

2

34

=

∞

@

A

•

`

I•@&’

A

‘ωš

Œ

4π

K ™‹

2

Q’

’ “Œ

∞

Учитывая, что

Œ

›

=

•

`I•@&’ŒA‘ω =

(2.13)1

’ “Œ

H

@ −

A

’ “Œ

2

=

`I “Œ@&’ ŒA − `

’I “Œ@&’ ŒA

=

2 sin(2π − π)

H @ −

A

@ −

A

∞

‹( )

получим выражение для

непрерывной функции

2:

2

‹( ) =

∞

=

4π Q’

2

@ −

2 A

∞

sin(2π − π)

(2.14)

K∞

‹ @

A

A

= K ‹ @

2

2π − π

Q’

Таким образом, непрерывная функция

‹( )

определена

всюду

по

её

•,(2π =

2π

значениям в точках отсчёта.

sin 2π

Функция

(

)

является

базисной

функцией

из

ряда

Котельникова

или

функцией

отсчётов.

Функция

отсчётов

обладает

)

следующими свойствами: принимает значение равное 1 при

и нулевые

значения во всех остальных точках отсчёта,

т.е. при

График данной

=

Œ

. = 0

функции представлен на рис. 2.1.

Спектр функции отсчетов постоянен в пределах полосы пропускания (от

0 до

Гц)

и

тождественно

равен

нулю

вне этой полосы. Пусть дана

произвольная

функция

времени,

спектр

которой

ограничен

частотой

.

¡T¢

’¡£ `

= cos + H sin

1 При выводе использовалась формула Эйлера, связывающая комплексную экспоненту с

sin

=

I

Iž

. В соответствии

тригонометрическими функциями следующим образом:

с данным выражением можно записать, что

T¢.

35

Определим значения этой функции в точках отсчета, отстоящих на расстоянии

Œ друг от друга (рис. 2.2).

Рис. 2.1. График функции отсчётов	•,(2π ) =	“Œ&
		¤¥¦( “Œ&)

Рис. 2.2. График произвольной функции времени, спектр которой ограничен
= ,	−		частотой
			< <			функция мала.		Пусть
2	Предположим, что вне		интервала
							2 + 1
		, тогда в интервале			количество точек отсчёта равняется
	если	отсчёты берутся в центрах		интервалов		отсчёта, и		, если

отсчёты берутся на краях интервалов. Значения функции в этих точках в соответствии с выражением (2.13) определяют саму непрерывную функцию.

36

Функция отсчётов •,(2¨ ) быстро затухает (рис. 2.1), следовательно,

влияние каждого члена в уравнении (2.13) ограничено малым числом

интервалов в окрестности соответствующей точки отсчёта. Таким образом,

если рассматриваемая произвольная функция всё-таки вне интервала			внутри
значима (предположение, сделанное ранее ошибочно), то её значения				< <
этого	интервала, за исключением самых её краёв – окрестностей точек			и , с
большей степенью точности определяются значениями функции в		2		точках
отсчёта.

Стоит отметить, что не может существовать функция, ограниченная во

времени и одновременно обладающая ограниченным спектром, поскольку если функция имеет спектр, строго ограниченный полосою конечной ширины, то её временное представление растягивается на неопределённо большой интервал,

хотя функция может оказаться очень малой. Однако возможно существование функции, которая принимает наибольшие значения (квадратичный эффект функции) в конкретных интервалах времени и полосы частот.

2.2. Теорема отсчетов в частотном‹( ) представлении

Рассмотрим функцию , тождественно равную нулю вне интервала от

до . Спектр данной функции в соответствии с прямым преобразованием Фурье будет иметь вид:

Ω(ω) = • ‹( )`’I•& d

(2.15)

$'

Разложим функцию ‹( ) в

ряд Фурье в интервале от

до

:

∞

‹( ) =

K ª `

I$(’$'

Q’

(2.16)

∞

“ &

Ω

(2.17)

ª =

1

1

c

2¨

d

• ‹( ) `’I$(’$' ‘ =

−

$'

−

−

37

Функция

полностью определяется её разложением в ряд Фурье в

ω = ω

#

ω

#

=

2π

Ω

в точках

−

интервале

‹( )

.

Следовательно, значения спектра

,

где

–

это угловая

частота,

а

n

принимает все

< <

(ω)

отрицательные и положительные2 1

целочисленные значения (включая 0) будут

полностью определять исходную функцию времени

.

частотном представлении

Исходя из вышесказанного, теорема отсчётов в ‹( )

< <

то Ω

‹( )

может быть сформулирована следующим образом. Если Ω

является

(ω)

интервала

,

спектром функции

, тождественно равной нулю вне

(ω)

однозначно определяется последовательностью ее значений в точках,

отстоящих друг от друга на расстоянии

$(’$'

Гц или на расстоянии, равном

∞

(”)

∞

∞

значению угловой частоты ω# = ( “ '.

Спектр Ω

является

комплексной функцией:

$ ’$

(2.18)

Ω

(ω) = • ‹( )`

’I•&

d = • ‹( ) cos(ω ) d − H • ‹( ) sin ω d

’

∞

’

∞

’

∞

Следовательно, Ω

является комплексным числом, для определения

которого

требуется

знание его вещественной и мнимой частей. Как можно

( ω#)

заметить

из

выражения (2.18),

величины Ω

и

Ω

являются

комплексно– сопряжёнными,

следовательно,

нет необходимости в

задании

(− ω#)

(+ ω#)

значений спектральной функции в области отрицательных частот, так как они могут быть однозначно определены по значениям в области положительных

частот. Если длительность сигнала приближенно составляет										,	а его
спектр приближённо ограничен частотой			и если				,	то спектральная
								=	−
функция сигнала весьма точно	определяется				её значениями в точках
				2 1
отсчёта, отстоящих друг от	друга на	расстоянии			$	Поскольку			при		всех
			( + 1) .

частотах, отличных от нуля, задание спектральной функции требует задания её вещественной и мнимой частей, общее число независимых данных,

необходимых для однозначного определения спектральной функции,

38

составляет

2 + 1 ≈ 2

,

т.е.

столько

же,

сколько и

при временном

представлении.

Аналитическое выражение для спектральной функции Ω

, заданной её

значениями в точках отсчёта, будет иметь вид:

(ω)

Ω

∞

Ω

2π

(2.19)

c

d

2

(ω) = K

ω

Q’

− π

∞

При выводе

уравнения

(2.19)

предполагали, что

$

и

$

.

2

Выражение в виде (2.1) определяет функцию

значений

,

в то

для любых= −

=

время как выражение в виде (2.15) –

интервале

. Во втором

только в ‹( )

случае функция определяется через значения её

спектральной функции в точках

< <

отсчёта на оси частот.

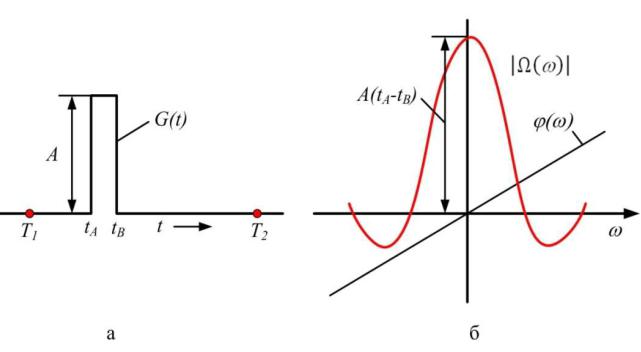
На рис. 2.3−а представлен прямоугольный импульс высотою A и

длительностью <. Данная< функция удовлетворяет условию равенства нулю вне интервала . На рис. 2.3б приведены модуль и фаза спектра функции.

Рис. 2.3. Импульсная функция времени (а) и ее спектральная функция (б)

39

	Для		точек	отсчёта, отмеченных		на	оси	частот	для интервала
			, можно определить значения модуля (с точностью до постоянного
множителя			$(’$'		коэффициентов		комплексного		ряда Фурье,
	< <		)	и фазы		< <		.
представляющие функцию ‹( ) в интервале

2.3. Преобразование отсчётных значений во времени в отсчётные значения

по частоте и обратное преобразование

Определим взаимосвязь между значениями функции в точках отсчёта на оси времени и на оси частот. Для этого еще раз запишем выражения для исходной и спектральной функций в виде ряда Фурье:

(ω) = ,(ω) − HN(ω) =

∞

‹ @

A `

’I•Œ

(2.20)

Ω

∞

2

K

2

‹( ) =

∞

Q’

K

c

d `

I$(’$'

−

−

= −

-Q’

∞ Ω

(2.21)

начало отсчета таким образом, чтобы

$ и

$, где

. Пределы суммирования (±∞) в уравнениях

(2.20)

и (2.21) можно

заменить

= −

=

на

(±WT), поскольку вне этих пределов слагаемые предполагаются

пренебрежимо малыми.

Пусть

” = ®S$ , = \Œ, тогда выражения (2.20) и (2.21) преобразуются в

выражения (2.22) и (2.23), которые являются формулами преобразования отсчётных значений во времени в отсчётные значения по частоте и обратно.

Ω c		d = 2	Q’ŒK $		‹ @2A `’I“SŒ$ = 2		Q’ŒK $ ‹ @2A cos @		A −	(2.22)
		− H	K	‹ @		A sin @πE A = , c2πEd − HN c2πEd
			Œ$		2
		2 Q’Œ$

40