Методическое пособие Теория информации-2

					(	) =	∞			− τ)‚(τ) dτ
							’• ²(		′		(4.80)
					′
²(	− τ)dτ	в		τ			∞
					в					(4.80) определяет возраст импульса
	Величина					уравнении
′			момент времени ′.							Данное уравнение называется интегралом

суперпозиции и представляет собой импульсивный отклик как взвешенную функцию импульсов в предыдущие моменты времени.

На функцию

‚( )

должны налагаться следующие два ограничения:

∙

при

→

, т.е. фильтр не может реагировать на импульс до его

подачи;

‚( )

→ 0

< 0 ‚( )

= 0

∙

при

∞

(ω)

, т.е. отклик на импульс затухает со временем.

передачи

и

обладающего

Квадрат амплитудно-частотной характеристики фильтра,

(ω)

(ω)

(4.81)

функцией передачи

, может быть выражен как произведение функции

комплексно-сопряжённой с ней функцией

.

Тогда, передаточная функция линейных фильтров представляет собой в общем случае отношение двух операторных полиномов:

| (ω)| =

= í

α

α

α

α

(4.82)

(ω–

)

(ω − β )(ω − β

)(ω − β

) …

где

и

)(ω − β

(ω)

(ω) ω

Функция

полиномы с действительными коэффицентами.

представляет

собой

комплексную

функцию

передачи

линейного фильтра с минимальным фазовым сдвигом и с заданной функцией передаточной функцией.

ω = í (ω − αβ )(ω − βα ) … (4.83)

Важное свойство цепи (представляющей собой линейный фильтр) с

минимальным фазовым сдвигом’(ωсостоит) в том, что обратная ей цепь (т.е. цепь с характеристикой передачи ) также физически осуществима.

111

’(ω) =			α	α				(4.84)
Таким образом, если	на вход фильтра				) …		подаётся сигнал	, то по
		í (ω −		)(ω −
						исходный сигнал,		пропустив
выходному сигналу возможно восстановить(ω)								²( )
выходной сигнал через обратный фильтр с характеристикой ’								. Более

(ω)

того, такое восстановление сигнала осуществляется без задержки во времени. В

случае цепей с неминимальным фазовым сдвигом построение физически осуществимой цепи, строго обратной по отношению к данной, невозможно.

4.4.3. Характеристики некоторых линейных фильтров

Рассмотрим характеристики ряда широко применяемых аналоговых непрерывных БИХ– фильтров: Баттерворта, Чебышева, инверсный Чебышева,

Кауэра, Бесселя.

Фильтр Баттерворта имеет амплитудно-частотную характеристику

(АЧХ), квадрат которой определяется соотношением:

•			ω	ωË + 1						(4.85)
					ωс – частота среза;			– порядок фильтра.
где ωË = •с –	относительная частота;
Все производные функции (4.85) по частоте								от первого до
порядка в точке			равны нулю.		Данный	фильтр		называют	фильтром		с
							ωË			(2 −	1)
максимально	гладкой АЧХ.
		ωË
Фильтр Чебышева имеет					АЧХ, которая		в	полосе	пропускания

характеризуется пульсациями одинаковой амплитуды, поэтому его часто называют фильтром равноволновых пульсаций. За пределами полосы пропускания АЧХ этого фильтра монотонно уменьшается, причём уменьшение АЧХ в этой области у фильтра Чебышева происходит более резко, чем у фильтра Баттерворта такого же порядка.

Квадрат АЧХ фильтра Чебышева определяется соотношением:

112

			ωË =
	(ωË)					β
где		–	первого рода -го порядка,				–
			полином Чебышева1 + β		(ωË)

постоянный коэффициент, задающий амплитуду пульсаций АЧХ.

Полином Чебышева -го порядка может быть найден рекуррентного соотношения:

(4.86)

некоторый

на основе

’

’

(4.87)

между

−1 < ° < 1

что в данном

соотношении

,

. В

Стоит отметить,

диапазоне

значения полинома Чебышева

волнообразно#

изменяются

(°) = 1

(°) = °

|°| > 1

уровнями

и

. При этом число полуволн на графике полинома на

порядка полинома. При

всегда имеем

;

при

единицу меньше −1

+1

монотонно и неограниченно возрастает

модуль полинома Чебышева

.

|°| = 1

| (°)| = 1

Инверсный фильтр Чебышева имеет АЧХ, которая монотонно изменяется

в пределах полосы пропускания и пульсирует в полосе заграждения. Эта АЧХ описывается соотношением:

| (ωË)| =	1 + β	ωË 1	(4.88)
		@ωËA

Фильтр Кауэра (эллиптический фильтр) имеет амплитудно-частотную характеристику, пульсирующую как в полосе пропускания, так и в полосе заграждения. Квадрат АЧХ этого фильтра имеет вид:

ωË

=

(4.89)

где

–

рациональная

функция, определяемая при чётных

соотношением:

Ö (ωË)

1 + β Ö (ωË)

Ö (°) =

(°

µ

,

(4.90)

где

í =

.

° − 1)(°

°

− 1) … (°

°µ

− 1)

рациональная функция, определяемая при чётных

При

нечётных

113

соотношением:

Ö (°) =

(°

µ

,

(4.91)

где í =

’)

.

°

− 1)(°

° − 1) … (°

°µ

− 1)

Ö (°)

обладает следующим свойством:

Функция

Параметры

Ö c

°

d

=

Ö (°)

(4.92)

таким

имеют значения больше 0 и меньше 1 и

выбираются

образомµ, что в промежутке

с

(где

с

)

° , ° , … , °

∆

между

нулем и

обеспечиваются

равноволновые пульсации

функции0 ≤ ° ≤ °

° < 1

некоторым значением .

При

этом

в полосе

пропускания

квадрат

АЧХ

Ö

(°)

± ((

эллиптического фильтра (4.89)

пульсирует между значениями

1 и

,

а в

полосе заграждения –

между значениями 0 и

± ((

∆

∆

.

Эллиптический фильтр в сравнении со всеми другими типами фильтров имеет наиболее крутой спад АЧХ при переходе от полосы пропускания к полосе заграждения.

Фильтр Бесселя отличается от других описанных фильтров тем, что имеет хорошую фазово-частотную характеристику (ФЧХ). Проходящий через фильтр сигнал не изменит своей формы, если все гармоники сигнала будут задерживаться в фильтре на одно и то же время. Поскольку фазовый сдвиг измеряется в долях периода рассматриваемой гармоники, то постоянство времени задержки равносильно линейной частотной зависимости фазового сдвига сигнала в фильтре.

Фильтр Бесселя обеспечивает наилучшее приближение реальной ФЧХ к идеальной линейной зависимости. Зависимость времени запаздывания от

114

частоты для фильтра Бесселя имеет такой же характер, как АЧХ для фильтра Баттерворта. Передаточная функция фильтра Бесселя определяется формулой:

‹(<) =		,	(4.93)
где ‚ < – полином Бесселя,	который может быть найден на основе равенств:
	‚ (<)	’
	’		(4.98)
			(4.94)
			(4.96)

Соотношение между АЧХ различных фильтров 4-го порядка представлены на рис. 4.9.

Рис. 4.9. АЧХ фильтров нижних частот 4– го порядка:

1 – Баттерворта; 2 – Чебышева; 3 – Бесселя; 4 – инверсный Чебышева; 5 – Кауэра

Для фильтров Чебышева, инверсного Чебышева и Кауэра АЧХ зависит не только от порядка фильтра, но и от принятых параметров, определяющих пульсации АЧХ. Сравнивая между собой различные типы фильтров, следует иметь ввиду, что фильтры, характеризующиеся более крутым спадом АЧХ в переходной полосе, имеют обычно большее время установления выходного сигнала при скачкообразном изменении входного.

115

5. Модуляция сигналов

Для передачи сигналов на большие расстояния необходимо, чтобы они обладали большой энергией. Известно, что энергия сигнала пропорциональна четвёртой степени его частоты, т.е. сигналы с большей частотой обладают большей энергией. В практике часто сигналы, несущие в себе информацию

(например, речевые сигналы) имеют низкую частоту колебаний и поэтому,

чтобы передать их на большое расстояние необходимо повышать частоту информационных сигналов. Добиваются этого путём «накладывания» информационного сигнала на другой сигнал, который имеет высокую частоту

колебаний.

Модуляция – тип физического кодирования, используемый при передаче

дискретных данных по каналам связи. Сущность модуляции, заключается в следующем. Формируется некоторое колебание (чаще всего гармоническое),

называемое несущим колебанием или просто несущей. Какой-либо из параметров этого колебания (амплитуда, частота, фаза) изменяется во времени пропорционально исходному сигналу. Исходный сигнал называют модулирующим, а результирующее колебание с изменяющимися во времени

параметрами – модулированным сигналом. Спектр результирующего

модулированного сигнала зависит от типа модуляции и скорости модуляции.

Обратный процесс – выделение модулирующего сигнала из модулированного колебания – называется демодуляцией.

Использование модуляции позволяет согласовать параметры сигнала с параметрами каналов передачи сигналов, повысить помехоустойчивость сигнала, увеличить дальность передачи сигнала, организовать многоканальную

передачу сигнала.

В настоящее время всё большая часть информации, передаваемой по разнообразным каналам связи, существует в цифровом виде. Это означает, что

		, , , …
передаче подлежит не непрерывный		(аналоговый) модулирующий сигнал, а
последовательность целых чисел		#	,	которые могут принимать
		116

значения из некоторого фиксированного конечного множества. Эти числа,

называемые символами, поступают от источника информации с периодом , а

hчастота² = 1/, соответствующаяj этому периоду, называется символьной скоростью

$ .

Последовательность передаваемых символов является, очевидно,

дискретным сигналом. Поскольку символы принимают значения из конечного множества, этот сигнал фактически является и квантованным, т.е. его можно назвать цифровым сигналом. В конце данной главы кратко будут рассмотрены вопросы, связанные с преобразованием этого цифрового сигнала в аналоговый модулированный сигнал. В случае цифрового сигнала используют термин манипуляция сигнала.

5.1. Классификация методов модуляции

В качестве несущего сигнала могут использоваться:

∙ гармоническое колебание, при этом модуляция называется аналоговой

или непрерывной;

∙периодическая последовательность импульсов, при этом модуляция называется импульсной;

∙постоянный ток, при этом модуляция называется шумоподобной.

Так как в процессе модуляции изменяются информационные параметры несущего колебания, то название вида модуляции зависит от изменяемого параметра этого колебания (например, амплитуда, частота, фаза).

Виды аналоговой модуляции:

∙амплитудная модуляция (АМ) – происходит изменение амплитуды несущего колебания;

∙частотная модуляция (ЧМ) – происходит изменение частоты несущего колебания;

∙фазовая модуляция (ФМ) – происходит изменение фазы несущего колебания.

117

Частотную и фазовую модуляции относят к классу угловых модуляций.

Виды импульсной модуляции:

∙амплитудно-импульсная модуляция (АИМ) – происходит изменение амплитуды импульсов несущего сигнала;

∙частотно-импульсная модуляция (ЧИМ) – происходит изменение частоты следования импульсов несущего сигнала;

∙фазо-импульсная модуляция (ФИМ) – происходит изменение фазы импульсов несущего сигнала;

∙широтно-импульсная модуляция (ШИМ) – происходит изменение длительности импульсов несущего сигнала.

Рассмотрим более подробно виды аналоговой модуляции.

5.2. Аналоговая модуляция
Рассмотрим гармоническое колебание, которое имеет частоту	,
достаточную для распространения сигнала на большие расстояния,	ωи
изменяется по закону:

(5.1)

Наложить информацию на это колебание можно! путёмωмедленногоφ, по сравнению с периодом, изменения его амплитуды , частоты или фазы . В

зависимости от того, какой параметр изменяют, как уже говорилось ранее,

различают амплитудную, частотную и фазовую модуляцию.

5.2.1. Амплитудная модуляция

Амплитудная модуляция (AM) является наиболее простым и распространённым способом изменения параметров носителя информации. При амплитудной модуляции огибающая4 гармонического колебания (переносчика)

изменяется по закону, совпадающему с законом изменения передаваемого

4 Огибающая – функция, описывающая изменения какого-либо параметра во времени, в данном случае – изменение амплитуды сигнала при постоянной частоте.

118

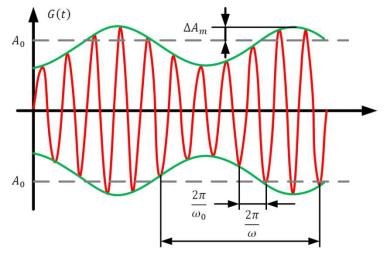
сообщения; частота же и начальная фаза колебания поддерживаются неизменными. Поэтому для амплитудно-модулированного колебания выражение (5.1) можно заменить на:

			#	#	(5.2)
Характер огибающей			определяется видом передаваемого сообщения.
Основным параметром	амплитудно-модулированного колебания является
		!( )

коэффициент модуляции. Если модулирующая функция (информационный сигнал) является гармоническим колебанием, описываемым уравнением:

И

#

И

И

(5.3)

!( )

то изменение амплитудной характеристики модулированного сигнала

можно представить выражением:

#

S

#

И

И

И

(5.4)

сигнала.

∆!S = í!#

где

И –

частота модуляции;

И – начальная фаза модулирующего сигнала;

–

коэффициент пропорциональности;

–

амплитуда

изменения

ω

φ

í

Рис. 5.1. Колебание, модулированное по амплитуде гармонической функцией

Отношение	F =	+	Таким
		∆Þ называется коэффициентом модуляции.

образом, мгновенное значение модулированного колебания можно описать

119

уравнением:

#	И	И	#	#	(5.5)
.		!SI = !#(1 − F)
При неискажённой модуляции		(F ≤ 1)	амплитуда колебания изменяется
!SÒÁ = !#(1 + F)	минимальной				до максимальной
в пределах от

Для определения технических характеристик канала связи необходимо установить связь между спектром модулированного колебания и спектром модулирующей функции (спектром исходного сообщения). Рассмотрим случай тональной (гармонической) модуляции для которого верно выражение:

#	И	И	(5.6)

Преобразуем уравнение (5.5) к виду:

#	#	#	И	И	#	#	(5.7)

Второе слагаемое в правой части выражения (5.7), являющееся результатом модуляции, можно привести к виду:

			= 2 cosa(ω# − ω				) + (φ# − φ		)b +		(5.8)
				F	И	И И	#	#И
			+ F cosa(ω# + ωИ) + (φ# + φИ)b
тогда выражение				(5.7) примет вид:
				2
‹	!# co			ω#	φ#	2	co ω#	ωИ		φ# φИ	(5.9)
			+ F!# cosa(ω# + ωИ) + (φ# + φИ)b
	Первое	слагаемое в (5.9) представляет собой исходное немодулированное
				2

колебание с частотой				. Второе и третье слагаемые соответствуют новым
колебаниям	(	гармоническим),				появляющимся	в	процессе	модуляции
			ω#
амплитуды.	Частоты		этих		колебаний (ω# − ωИ)		и	(ω# + ωИ)	называются
						120