Методическое пособие Теория информации-2

	‹ @	A =		K	Ω c		d `I“Œ-$\ =		(2.23)
= 1 ,(0)	Œ$2			-Q’Œ$			Œ$
	+ 2 K , c2πJd cos @πJ<A					+ 2 K N c2πJd sin @πJ<A
	-Q						-Q

Выражения (2.22) и (2.23) представляют собой линейные алгебраические

уравнения с постоянными коэффициентами.

2.4. Распределение вероятностей для непрерывных величин. Эргодические

ансамбли функций. Когерентность

В теории информации непрерывные сигналы (как и дискретные)

характеризуются вероятностью их появления. Теорию непрерывных сигналов можно рассматривать как предельный случай теории дискретных сигналов.

Согласно теореме отсчётов во временном представлении, рассмотренной ранее,

независимо друг от друга могут быть выбраны значения сигнала только в точках отсчёта, что делает непрерывный сигнал аналогичным конечной последовательности символов. Стоит отметить, что на всякий непрерывный сигнал всегда накладывается шум, вследствие чего количество различимых уровней сигнала становится конечным. Это делает совокупность значений

непрерывного сигнала эквивалентной конечному алфавиту.
Если	– непрерывная случайная величина, то вероятность того, что при
функцией плотности		°	° + d°				(°) d°
некотором	°конкретном испытании значение данной величины окажется
заключённым между		и		, будет равна величине				, называемой
		вероятностей. Поскольку величина					принимает значения
в интервале от – ∞ до +∞, то функция распределения					плотности вероятностей
						°

может быть определена как:

’• (°) d° = 1
∞
	(2.24)
∞
41

функций.

° , ° , … , °			вероятностей функции			переменных
Распределение плотности
	определяется аналогично:			d° = 1
						(2.25)
Величина ° , ° , … , ° в выражении (2.25) является функцией
распределения плотностей		вероятностей,		характеризующей вероятность
одновременного появления		переменных		° , ° , … , ° . В	случае, когда

непрерывные случайные величины независимы, можно записать равенство

(2.25)2.		’• ° d° = =		’• ° d° = 1
’• ° d° =
∞		∞		∞
∞		∞		∞		(2.26)

В случае, когда распределение одной непрерывной величины зависит от распределения другой, говорят о наличии связей между ними.

Совокупность функций, обладающих одним или несколькими характерными свойствами, называется множеством функций. Множество функций, заданное вместе с плотностью вероятности, характеризующей вероятность появления отдельных функций множества, называется ансамблем

Множество синусоидальных функций ² = ! sin ω + φ образуют ансамбль если задано распределение вероятностей !, ω, φ определяющее вероятность, одновременного появления случайных величин !, ω, φ. Если любая

из данных величин для всех функций ансамбля остается неизменной, то такая величина не является случайной. Случайные величины ансамбля функций называют его степенями свободы. Если какая– то из величин ансамбля полностью определяется значениями других величин, то в этом случае она не является не зависимой степенью свободы ансамбля.

				42		∙ °		∙ … ∙		°
2	° , ° , … , °			= °
	Поскольку для независимых случайных величин справедливо:									.

Введём понятие эргодического ансамбля функций. Если можно считать,

что функции ансамбля обладают спектром, ограниченным полосой пропускания , то в соответствии с теоремой Котельникова некоторая частная

функция	данного ансамбля будет определяться			её значениями в точках
отсчёта (количество степеней свободы данного		ансамбля равно				).
			2
Эргодический ансамбль функций времени с				ограниченным спектром
					2

представляет собой ансамбль таких функций, значения которых в точках отсчёта образуют эргодическую систему символов. В эргодическом ансамбле функций полная сумма вероятностей появления функций, значения которых в точках отсчёта образуют 2эргодические последовательности, равна единице.

Количество точек отсчёта в типичной функции эргодического ансамбля должно быть велико. Взаимные связи между отдельными значениями функций

в эргодических ансамблях должны сказываться лишь при конечном расстоянии

между ними. Присущие ансамблю плотности вероятностей не должны зависеть
от времени и, следовательно, от выбора точки отсчёта на временной оси.
Рассмотрим два сигнала		и ‹ .	Если зная сигнал ‹ , можно
информацию			о сигнале	, то эти сигналы
почерпнуть из него какую-либо‹	( )			‹

(по крайне мере частично) зависимы. Такая зависимость между значениями двух сигналов (в точках отсчёта), несущими в себе заключённую между сигналами информацию, называется когерентностью. Таким образом, два сигнала или две части одного сигнала называются когерентными, если между значениями этих сигналов имеется функциональная зависимость. Два сигнала или две части одного сигнала не когерентны, если они функционально не зависимы.

Пусть даны два сигнала, значения которых в точках отсчета:

… ´’, ´#, ´ , ´ , …	(2.27)
Тогда, если плотность вероятностей в некоторой точке °µ зависит от
значений сигнала в одной или нескольких точках	´, то можно сказать, что
43

сигнал

в той или иной мере ограничивает сигнал

. На практике часто в тех

случаях´, когда сигнал

ограничивает

сигнал

´

, °имеет место

и обратная

°

°

влияет на сигнал

°

зависимость: сигнал

´

°

, то сигнал

частично когерентен с сигналом .

Если сигнал

полностью

°

´

´

´

°

,

и, зная величину

определяется сигналом

, можно определить все свойства ,

то сигнал

полностью

когерентен с сигналом .

°

´

´

Общеизвестно, что при сложении «в фазе» двух одинаковых сигналов их

суммарная энергия (квадратичный эффект

) возрастает вчетверо по

сигналов. Напротив, при сложении

сравнению с энергией каждого из исходных¶a‹( )b

d

тех же сигналов «в противофазах» они взаимно уничтожаются и квадратичный эффект суммарного сигнала оказывается равным нулю. В общем случае

суммарный эффект	двух сигналов	‹ ( )	и	‹	будет соответствовать
выражению:
	•a‹ + ‹ b d =					(2.28)
= •·a‹ b + a‹ b ¸ d + • 2 ∙ ‹ ∙ ‹ d

Первый интеграл в правой части выражения (2.28) является суммой квадратичных эффектов каждого из сигналов, а второй интеграл – квадратичный эффект, характеризующий взаимодействие между сигналами.

Если квадратичный эффект взаимодействия равен нулю, то сигналы ‹ и ‹ называют ортогональными.

Отношение

|

|

∙

|

|

d

= •

2 ¶

‹

‹

‹

(2.29)

называется отношением взаимодействия между сигналами

и

‹ .

Величина может

• принимать любые значения, в интервале между –1

и +1.

Определим

выражение

квадратичного эффекта взаимодействия

между

двумя сигналами через значения этих сигналов в точках отсчёта на оси частот.

44

Предположим, что постоянные составляющие в сигналах или хотя бы в одном из них отсутствуют. Тогда можно записать:

‹ ( ) =

∞

, c

d cos c

d + N c

d sin c

d

(2.30)

∞K

Q

‹ ( ) = K

, c

d cos c

d + N c

d sin c

d

(2.31)

Q

Как было рассмотрено ранее, коэффициенты a и b с точностью до

Поэтому

$

‹ ( )

‹ ( )

множителя

совпадают с коэффициентами рядов Фурье для

и .

будет справедливо равенство:

∞

• ‹ ( ) ∙ ‹ ( ) d =

(2.32)

#

= 2 K , c2π d , c2π d + N c2π d N c2π d

Q

‹ ( )

и

‹ ( )

принадлежат к независимым друг от друга

эргодическим

Если сигналы

ансамблям, то квадратичный эффект взаимодействия оказывается

равным нулю:

∞

∞

K , c

d , c

d =

K N c

d N c

d = 0

(2.33)

Q

Q

Квадратичный эффект взаимодействия можно выразить также через значения сигнала в точках отсчёта на оси времени:

					S	2		2
∙	sin(2π − π)		∙	sin(2π − Eπ)				d =	(2.34)
	2π − π			@	2π − Eπ		A
	= 1	K ‹			A ∙ ‹ @
	2			2		2

Таким образом, можно сделать вывод, что при сложении некогерентных

45

сигналов, являющихся типичными функциями эргодических ансамблей в линейной системе, их квадратичные эффекты подчиняются аддитивному закону. Поскольку квадратичный эффект взаимодействия некогерентных сигналов, входящих в эргодические ансамбли, обращается в нуль, то отличие данного эффекта от нуля свидетельствует о зависимости этих сигналов друг от друга при условии, что постоянные составляющие в сигналах отсутствуют.

2.5. Преобразование связей во времени в связи по частоте

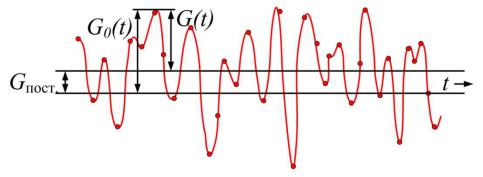
Данный материал будет изложен кратко, без приведения полных математических выкладок. Запишем, как взаимные связи во времени преобразуются в связи между амплитудами частотного спектра. Пусть дан ансамбль функций, ограниченных частотой‹ ( ) W. На рис. 2.4 представлена типичная функция данного ансамбля # . Точками отмечены значения функции в точках отсчёта… ’ , ’ ’ , … , #, , … , µ, … , ….

Рис. 2.4. Типичная функция ансамбля функций, ограниченных частотой W

Если распределение вероятностей величины ‹# @ µ A, представляющее

µ Œ

собой значение функции в точке , зависит от значений функции в

предыдущих или последующих точках, то в ансамбле имеются связи между
значениями функции в различных точках отсчёта. ‹пост. на рис. 2.4 – есть
среднее значение функции ‹# за достаточно длительный период времени .
Определим новую функцию ‹ = ‹# − ‹пост.. При	→ ∞ спектры функций
46

‹( )	и	‹#( )		совпадают	друг с другом		за исключением	значений нулевой
частоты.						‹( )		µ
									в некоторой
	Аналогично, если распределение вероятностей для
точке		не		зависит от	значений			отсчётаŒ		, то связи
							в других точках‹ @		A
отсутствуютµ			и значения		в её точках отсчёта не коррелированны. В этом

‹( )

случае для эргодических ансамблей распределение вероятностей не зависят от

выбора начала отсчёта времени. Поэтому в отсутствии связей распределения

‹ @	A							‹( )
вероятностей во всех точках одинаковы. Если распределение вероятностей для
коррелированны‹(.			)						‹( )
µ		каким– либо образом зависит от значений								в других точках отсчёта,
то вŒ	функции			имеются связи		и значения					в её точках отсчёта
	Для значений функции ‹( ) в точках отсчета справедливо равенство:
				K	‹ @	2	A = 0
				2 Q’Œ$							(2.35)

Спектр мощности может быть записан следующим образом:

	(ω) = 2	∞	‹ @2A `	’i•Œ
Ω		∞
		KQ’

Влияние временных связей на спектр мощности функции выразить следующим уравнением:

¹c d¹ = 4 K º‹ @2A» +

+1 ΩK cos @πJ<A —K ‹ @ A ‹ c + <d˜ +

2 \ 2 2

+1 K cos @πJ<A —K ‹ @ A ‹ c + <d˜ 2 \ 2 2

(2.36)

‹( ) можно

(2.37)

Последние два слагаемых в правой части уравнения (2.37) отличаются

47

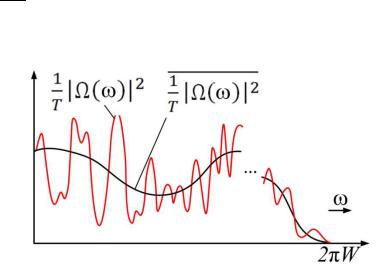
тем, что суммирование в первом случае ведётся по тем значениям p, при которых сказываются временные связи, а во втором – по значениям p, при которых временные¼ @ A¼ связи уже не сказываются. На рис. 2.5 приведен график

функции $ Ω “$- для типичной функции эргодического ансамбля. Точками

на графике отмечены значения спектра мощности в точках отсчёта.

Рис. 2.5. Спектр мощности некоторой функции $ ¼Ω @“$-A¼ и средний по

ансамблю спектр мощности

Из анализа уравнения (2.37) можно сделать следующие выводы:

1.Если взаимные связи между значениями функции в различных точках отсчёта на оси времени отсутствуют, то среднее по ансамблю значение спектра мощности в пределах полосы пропускания W остаётся постоянным.

2.При наличии временных взаимных связей среднее по ансамблю значение спектра мощности меняется с частотой.

3.Для конкретной функции ансамбля| (ω)| взаимные связи во времени не определяют конкретных значений Ω в различных точках отсчёта на оси

частот.

Рассмотрим связи между фазами составляющих частотного спектра.

Разложим типичную функцию эргодического ансамбля						в	спектр и
					отсчёта:
рассмотрим фазу φ- спектральной функции Ω(ω) в q-й точке‹( )
Ω c		d = ¹Ω c		d¹ `i½¾			(2.38)
			48

Поскольку все свойства ансамбля не зависят от выбора точки начала отсчета на временной оси, то все2πфазы для всех функций ансамбля распределены равномерно между 0 и . Запишем спектральную функцию в комплексном виде:

Ω

(2.39)

Так как все фазы равновероятны, то в среднем по ансамблю получим:

, c d			= N c d			= 2	Ω c d			(2.40)

Природа взаимных связей между отдельными спектральными составляющими в эргодических ансамблях функций времени такова, что распределение вероятностей как в отдельных точках отсчёта, так и в группах точек отсчёта оказывается соответствующим эргодической природе ансамбля.

Взаимные связи между фазами спектральных составляющих могут зависеть от частоты этих составляющих.

2.6. Энтропия непрерывного распределения						<(°) одной переменной ° можно
Энтропию непрерывного распределения
определить как:
	O = ∆ÁlimT→# Â− K <(°I) ∆°I loga<(°I)∆°IbÃ						(2.41)
		I			от – ∞ до +∞ разбит на малые
где весь интервал возможных значений
интервалы		. При вычислении	энтропии непрерывного				распределения
				°
	логарифмы по основанию e.
применяют ∆°I
виду: Выражение (2.44) при условии равенства интервалов ∆°I							преобразуется к
O = ∆ÁlimT→#	Â− K <(°I) ∆°I loga<(°I)bà + ∆ÁlimT→# Â− K <(°I) ∆°I loga∆°Ibà (2.42)
	I					I
			49

∆ÁT→# I

I

I

I

= − • <(°) log <(°) d° − lim

loga∆° b K <(° )∆° =

(2.43)

∆ÁT→#

I

I

I

I

= − • <(°) log <(°) d° − lim loga∆° b • <(°) d° =

∆ÁT→#

I

Ib

=

− ¶ <

°

log <

°

T

d° − ∆Álim→# loga∆°

∆Álim→# loga∆°

→

Заметим, что

T

Ib

∞,

но для непрерывных сообщений одно и

то же бесконечное слагаемое фигурирует дважды: со знаком (+) и со знаком (–).

Таким образом, данное слагаемое обращается в ноль и энтропию непрерывного распределения можно записать, как:

O = − • < ° log < ° d°

(2.44)

Для n переменных энтропию можно записать следующим образом:

O = • … • < ° , … , ° log < ° , … , ° d° … d°

(2.45)

Энтропия непрерывного распределения обладает теми же свойствами, что и энтропия дискретного распределения. Для эргодического ансамбля с ограниченным спектром введём понятие энтропии на степень свободы. Под числом степеней свободы понимается число независимых переменных, т.е.

количество точек отсчёта. Вследствие наличия взаимных связей степеней свободы может быть меньше, чем точек отсчёта.

энтропия

∞

1

O =

степень свободы =

(2.46)

= − →lim

• … • <

log <

° , … , °

° , … , °

d° … d°

где ° , ° , … , ° –

значения сигнала в точках отсчёта.

Поскольку = 2

,

то можем выразить энтропию на единицу времени

следующим образом:

50