Методическое пособие Теория информации-2

следовательно, при представлении его в частотной области обладает неограниченным спектром. Однако в силу свойств реальных источников сигналов и ограниченности полосы пропускания реальных каналов спектр сигнала с той или иной степенью точности можно считать ограниченным некоторой предельной частотой W. Обычно W определяется на основе энергетического критерия. Спектр ограничивается областью частот от 0 до W, в

которой сосредоточена подавляющая часть энергии сигнала (80–95 %). Такое

ограничение спектра, естественно, приводит к искажению сигнала.

Пример. Аппроксимировать прямоугольный импульс длительностью

и

амплитудой

рядом

Котельникова,

ограничивая его спектр частотой

Затем восстановить сигнал по отсчётам Котельникова.

SÒÁ

.

!

“

>

ω

Определим= $

интервал дискретизации из соотношения

.

Тогда

∆

∆ =

ωSÒÁ = “&

. Импульс аппроксимируется тремя отсчётами в моменты времени

. В данные моменты времени значения восстановленного сигнала

совпадают с значением исходного сигнала, т.е. будут равны

амплитуде

−

,

0,

!

(импульс прямоугольный).

,

†

Найдём

значения сигнала

в

промежуточных

точках

,

и

.

; , ;

;

SÒÁ

sin 2π

@1 + 1 A

∆

∆

1

sin ω

∆

1

‹

c

d = K ‹

−

= ‹ c−

d

2π

1

4

1

2

+

4

ω

SÒÁ

−

2

− 0A

−

A

@4

+ 2

A

+‹ 0

sin 2π @1

+ ‹ c1

d

sin 2π @1

1

=

2π

1

4

− 0A

2π

1

4

1

2

@4

sin @−

2

@4

− 2

A

= ! ™

sin 3π

+

sin π

+

πA

3π2

π 2

@−

π

2

š 1.061 ∙ !

2

2

2A

61

‹c3 d 0.552 ∙ !

‹( 4 ) 0

‹c54 d −0.144 ∙ !

‹c32 d 0

= 0 Исходный сигнал симметричен относительно момента времени

, той же симметричностью будет обладать и восстановленный сигнал. На рис. 3.2 показан исходный и восстановленный сигналы.

Рис. 3.2. Иллюстрация к примеру: прямоугольный импульс и его восстановленное

значение

Относительная точность восстановления сигнала γ может быть определена из соотношения:

						∞	Ω		= (ω)
		′			γ = #Œ			(ω) dω
					¶		Ω			′	(3.5)
	–(ω)					∞
где				–	энергия отброшенных высокочастотных составляющих сигнала;
(ω)			полная энергия сигнала.
		Таким образом, восстановление ограниченного во времени сигнала по
								62

отсчётам, полученным по теореме Котельникова при условии принудительного ограничения спектра сигнала, возможно только приближённо. Ошибка возникает не только за счёт принудительного ограничения спектра, но и за счёт конечного числа отсчётов в интервале2 времени Т, которых в соответствии с теоремой Котельникова будет . Эта составляющая является следствием пренебрежения вкладом бесконечного числа функций отсчёта,

соответствующих выборкам за пределами интервала Т .

Кроме того, процедура восстановления сигнала в данном случае вносит весьма существенную дополнительную погрешность. Она возникает потому,

что невозможно обеспечить создание импульсов бесконечно малой длительности, как невозможно осуществить их передачу по реальным каналам связи. Максимум выходного сигнала, соответствующего реакции идеального фильтра низких частот, запаздывает на время, равное бесконечности. Таким образом, за конечное время Т каждая функция отсчета, а следовательно, и их сумма, представляющая собой исходный непрерывный сигнал, будут сформированы лишь приближённо и тем более приближенно, чем меньше Т.

3.3. Дискретизация по критерию наибольшего отклонения
В процессе дискретизации непрерывная функция		,	имеющая
ограниченных производных, аппроксимируется	многочленом n– й степени. В
		‹( )		( + 1)

зависимости от выбранного способа восстановления он может быть интерполирующим или экстраполирующим. Задача обеспечения минимальной погрешности при восстановлении сигнала на практике не ставится. Обычно

указывается её допустимое значение

.

Погрешность восстановления δε#

функции

многочленом

( )

на

каждом участке аппроксимации

определяетсяÕ

остаточным членом

:

( )

∆

‹( )

‹

δÕ

Ö ( )

(3.6)

Ö( ) Следовательно≤ ε , шаг дискретизации должен быть выбран из условия

#. Выбор аппроксимирующего многочлена более высокой степени при

63

малой допустимой погрешности ε# обеспечивает меньшее число отсчётов,

однако при этом существенно возрастает сложность технической реализации метода. Поэтому обычно ограничиваются многочленами нулевой, первой и второй степеней (ступенчатая, линейная и параболическая аппроксимации соответственно). В качестве интерполирующих многочленов чаще других используются многочлены Лагранжа, а в качестве экстраполирующих – многочлены Тейлора.

3.3.1. Дискретизация с использованием интерполирующих многочленов

Лагранжа

Интерполирующий многочлен Лагранжа при равномерной дискретизации может быть записан следующим образом:

				‹ ( ) = ( ) =	×(λ − m) K(−1)i				i	,	(3.7)
где				+.	! iQ#	iQ#		λ − m
		∆
	λ =	&’&
			&							можно записать
	Тогда остаточный член Ö многочлена Лагранжа
следующим образом:						F±
											(3.8)
где F± –				Ö = |‹ − | ≤ + 1 ! ›×µQ# − µ › ,
				максимальный во всём интервале преобразования модуль + 1
производной сигнала ‹ .
	Определим шаг равномерной дискретизации на основе интерполирующих

многочленов Лагранжа нулевой степени. Значение восстанавливающей
функции ‹ в любой момент времени t на каждом j– м интервале i’ ≤ t ≤ i
принимается равным отсчёту	‹hij (рис. 3.2).
Соотношение (3.8) позволяет получить выражение для остаточного члена:
#		#	(3.9)
		64

Рис. 3.2. Схема равномерной дискретизации сигнала на основе интерполирующих

многочленов Лагранжа нулевой степени

Максимальное значение− =остаточного члена пропорциональноε шагу дискретизации, т.е. при # ∆ . Оно не должно превышать #. Отсюда вытекает условие, определяющее шаг дискретизации:

		∆					(3.10)
Если проводить	восстановление			сигнала			по двум отсчетам,
			F			‹( )
пользуясь функциями:
‹ ( ) =		i	2	i’	,		(3.11)
где ƒ i’ ; i„, то при		том		шаге дискретизации погрешность
			же

восстановления сигнала уменьшится вдвое (рис. 3.3).

Рис. 3.3. Схема восстановления дискретизированного сигнала по двум отсчетам при

его интерполяции многочленом Лагранжа нулевого порядка

65

Определим шаг равномерной дискретизации сигнала с помощью интерполирующих многочленов Лагранжа первой степени. В этом случае значение остаточного члена принимает вид:

#

Максимальное значение2!для остаточного члена

#

Тогда:

| − #|

= | − | =

&'’&+ = ∆ .

условии, что фиксированное значение

равноудалено от

Ö

Ö SÒÁ( ) ≤ 2 Ù

# 4

#

Ù =

8

∆

(3.12)

( ) достигается при и , т.е.

(3.13)

Учитывая неравенство (3.13), получаем ограничение на шаг

дискретизации:

∆ ≤ Ú

i’

i

„

F#

i

‹( )

i’

j

(3.14)

прямой

ƒ

;

‹h j

‹h

При восстановлении

исходного сигнала

на

каждом интервале

времени

используются два отсчёта

и

. Они соединяются

линией (рис. 3.4).

Рис. 3.4. Схема восстановления дискретизированного сигнала по двум отсчётам при

его интерполяции многочленом Лагранжа первого порядка

66

Сравнивая рис. 3.3 и 3.4 можно заметить, что при интерполяции

дискретизированного сигнала многочленом Лагранжа первой степени

погрешность восстановления ниже.

3.3.2. Дискретизация с использованием экстраполирующих многочленов

Тейлора

Экстраполирующий многочлен Тейлора определяется выражением:

‹( #) + ‹′( #)( − #) +

‹ ( #)( − #) + +

‹( )( #)( − #) +

‹( )2!

# с!ошибкой:

(3.15)

′′

и экстраполирует функцию

в окрестности точки

Ö ( ) = ‹( ) − ( ) =

#

#

( − #)±,

(3.16)

где

0 < Ü < 1

.

( + 1)!

Максимальная ошибка (максимальное значение остаточного члена)

определяется неравенством:

# ±

Ö

≤

(3.17)

Определим

шаг

равномерной дискретизации сигнала на основе

‹

( )

( + 1)!

многочлена Тейлора нулевой степени. Значение восстанавливающей функции

в любой

момент

времени

t на каждом

j– м интервале

i’ ≤ t ≤

i,

принимается равным

#

i’

(рис. 3.5).

Значение остаточного‹( ) = члена‹h

jдостигает

максимума в конце

интервала

(при = i):

# SÒÁ

i

i’

∆

(3.18)

В этом случае ограничение на шаг дискретизации следующее:

∆

F 67

(3.19)

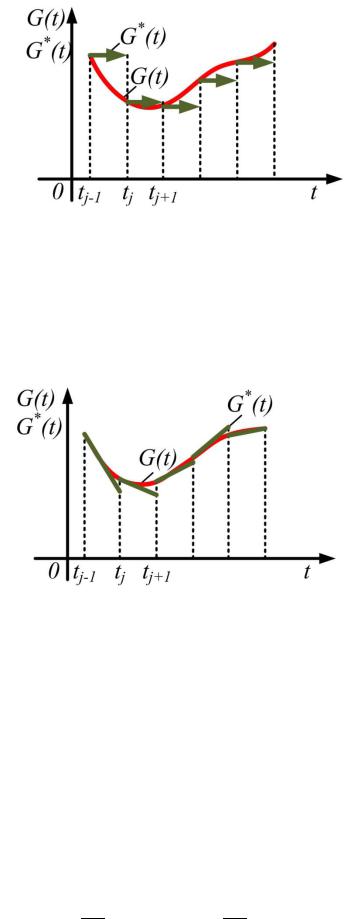
Рис. 3.5. Схема равномерной дискретизации сигнала на основе многочлена Тейлора

нулевой степени

Определим шаг равномерной дискретизации сигнала с помощью

многочлена Тейлора первой степени (рис. 3.6).

Рис. 3.6. Схема равномерной дискретизации сигнала на основе многочлена Тейлора

первой степени

При восстановлении сигнала

‹(в)

помимо отсчета

‹( #)

используется

значение первой производной

′

момент времени

.

Значение

#

#

i’

остаточного члена определяется неравенством:

=

‹

(

)

h

i’j

(3.20)

:

Максимум значения остаточного члена достигается при условии

SÒÁ ≤

2!

∆

= i

2

h i − i’ j =

2

(3.21)

68

Из неравенства (3.21) получаем ограничение на шаг дискретизации:

∆ ≤ Ú
		#	(3.22)
Восстановление сигнала	происходит без задержки во времени
		F

(рис. 3.6). Однако по сравнению с интерполяционным методом для него требуется вдвое большее число отсчётов.

3.4. Адаптивная дискретизация сигнала

Если ранее рассмотренные методы и алгоритмы дискретизации были рассчитаны на все множество возможных реализаций сигнала и потому опирались на предельные значения его динамических характеристик, то при адаптивной дискретизации ориентируются на динамические характеристики конкретной реализации сигнала, что позволяет получить минимальное число выборок, обеспечивающих восстановление этой реализации с заданной точностью.

В основе принципа адаптивной дискретизации лежит непосредственноеε слежение за текущей погрешностью восстановления сигнала #. Наиболее

широкое применение на практике получили алгоритмы дискретизации сигнала с адаптацией по длине интервала аппроксимации. В процессе последовательного ‹наращивания( ) интервала аппроксимации‹ ( ) производится сравнение сигнала с воспроизводящей функцией , формируемой с учётом текущих значений динамических характеристик εсигнала. Когда погрешность восстановления достигает заданного значения #, наращивание интервала прекращается и производится отсчёт. Интервалы времени между отсчётами при этом оказываются произвольными.

В качестве воспроизводящих функций наиболее часто используются степенные алгебраические полиномы нулевой и первой степеней:

‹ ( ) = K ,i i	(3.23)
iQ#69

		‹ ( ) = K ,i( − #)i,	(3.24)
где ,i		iQ#
	действительные коэффициенты.
	При–	этом возможны как интерполяционные,	так и экстраполяционные

способы адаптивной дискретизации сигнала. Интерполяционные способы не нашли широкого применения, поскольку их реализация связана с запоминанием сигнала на интервале аппроксимации и выполнением большого числа вычислительных операций. Поэтому ограничимся рассмотрением примеров адаптивной дискретизации сигнала на основе экстраполяции. ‹( )

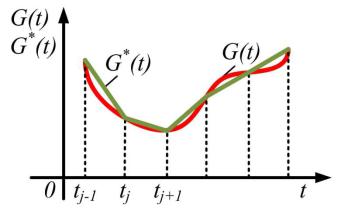
Проведём адаптивную дискретизацию реализации сигнала ,

изображенного на рис. 3.7, с использованием степенного алгебраическогоε полинома нулевой степени. Наибольшее допустимое отклонение равно #.

Рис. 3.7. Адаптивная дискретизация сигнала с использованием степенного

алгебраического полинома нулевой степени

На момент

i

начала каждого интервала аппроксимирующий полином

(

)

#

)

i

i

Õ

= ‹(

j

δÕ

#

ε

#

(3.25)

− ‹h

и

вычисляем

( ) = ,

принимаем

равным

разность

δ

с

. Установление равенства

‹

, которую сравниваем‹h

j

соответствует

моменту

i±

окончания

интервала и

проведения

очередного

отсчёта. Результаты

дискретизации отображены на рис. 3.7.

70