Методическое пособие Теория информации-2

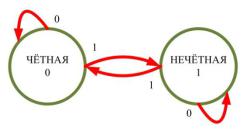
Предположим, что вероятность ошибки в каждой двоичной позиции равна и что ошибки в различных позициях независимы. Тогда, при N g,

вероятность одиночных ошибок равна N , а вероятность двойных

B gV

ошибок равна > , что приблизительно соответствует половине квадрата

вероятности одиночной ошибки. Таким образом, оптимальная длина

проверяемого сообщения зависит как от требуемого уровня надёжности, так и от вероятности появления единичной ошибки в любой позиции.

Подсчёт числа единиц производят следующим образом: в первых N − 1

позициях сообщения каждое число делится на 2 (основание) и заменяется остатком (0 или 1), затем результат помещается в -ую позицию. Для реализации

подсчёта применяют конечный автомат с двумя состояниями

(рис. 6.3). Автомат начинает работу в состоянии 0 и меняет его каждый раз при появлении 1. Состояние автомата в конце сообщения даёт окончательную чётность.

Рис. 6.3. Автомат для вычисления чётности

Стоит отметить, что на практике наиболее часто осуществляют проверку на нечётность (подсчёт числа нулей), чтобы сообщение (состояние из всех нулей) не считалось бы верным.

При разбиении сообщения на блоки, состоящие из N − 1 проверяемых символов и одного добавляемого символа, к последнему блоку при необходимости добавляют нули. Такое кодирование приводит к избыточности,

равной B = 1 + B. Для снижения избыточности требуется применять длинные последовательности символов, а для повышения надёжности –

151

короткие. Таким образом, выбор оптимальной длины кодируемой последовательности является точкой компромисса.

Простые коды для обнаружения пакета ошибок

Ошибки (шум) в принятых сообщениях часто группируются в пакеты, а

не в отдельные изолированные позиции. Пусть экспериментально получена максимальная длина пакета ошибок, который должен быть обнаружен.

Примем допущение, что длина пакета ошибок совпадает с длиной слова. В

этих условиях необходимо выбрать код с обнаружением ошибок и вместо вычисления проверок на чётность по битам провести вычисление проверки на чётность по словам. Работа со словами приводит к независимым кодам, по одному для каждого двоичного символа в слове.

Длина кодируемой последовательности символов P должна удовлетворять условию 0 ≤ P ≤ , тогда в случае перекрывания пакетом конца одного слова и начала другого, ошибки будут обнаружены.

Пример. Сообщение Fall 1980 можно закодировать кодом ASCII для исправления пакетов ошибок следующим образом:

F	=	106
a	=	141
l	=	154
l	=	154
space =		040

=	01 000 110	1	=	061	=	00 110 001
=	01 100 001	9	=	071	=	00 111 001
=	01 101 100	8	=	070	=	00 111 000
=	01 101 100	0	=	060	=	00 110 000

=00 100 000

Для данного пакета проведём побитовое сложение по модулю 22.

Контрольная сумма BEL=00 000 111. Таким образом, закодированное сообщение будет иметь вид Fall 1980 BEL, где BEL – это символ кода ASCII

для 00 000 111.

2 Побитовое исключающее ИЛИ (или побитовое сложение по модулю два) – это бинарная операция, действие которой эквивалентно применению логического исключающего ИЛИ к каждой паре битов, которые стоят на одинаковых позициях в двоичных представлениях операндов. Другими словами, если соответствующие биты операндов различны, то двоичный разряд результата равен 1; если же биты совпадают, то двоичный разряд результата равен 0.

152

Буквенно-цифровые или взвешенные коды

Предыдущие коды для обнаружения ошибок предполагали наличие простого белого шума. Однако существует ряд ошибок, возникающих из-за человеческого фактора, например, замена 0 и символа о, перестановка соседних

цифр при записи чисел и др.

Достаточно часто встречаются ситуации, в которых полный набор исследуемых символов равен 26 символам латинского алфавита, 10 цифровым значениям (арабская запись чисел) и пробелу, что в сумме дает 37 символов.

Для таких небольших наборов может быть применён следующий метод

кодирования. Символы сообщения снабжаются весами 1,2,3,…, начиная с

проверочного символа. Затем берётся остаток от деления суммы на 37 так,

чтобы проверочный символ мог быть выбран таким образом, чтобы вся сумма была сравнима с 0 по модулю 37. При этом суммирование проводят путём

нарастающего цифрования.
	Пример. Пусть 0=0, 2=2, .., 9=9, A=10, B=11, …,		Z=35, пробел=36.
Требуется провести кодирование сообщения A6 7. Проведем взвешенное
суммирование (табл. 6.8).
				Таблица 6.8
	Вычисление взвешенной суммы
	Символ кодируемого сообщения	Сумма		Сумма сумм
	A = 10	10		10
	6 = 6	16		26
	пробел = 36	52		78
	7 = 7	59		137
	x=x (дополнительный символ проверки)	59+x		196+x

		9Ci	=	5 11 +
		cj
Остаток	от деления	11 +		должен делиться на 37 без	остатка,
следовательно,	11 + = 37 = 26,			что соответствует символу	Q. Тогда

исходное сообщение будет кодироваться следующим образом: A6 7Q.

Проведём проверку правильности сообщения:

153

A	10Х5=50
6	6Х4=24
пробел	36Х3=108
7	7Х2=14
Q	26Х1=26
Σ	222=37Х6=0 по модулю 37

Данные коды наиболее часто применяются для проверки правильности номеров кредитных карт, ISBN книг и в других аналогичных ситуациях.

6.2.2. Корректирующие коды

Построение кода для передачи информации по каналу с помехами достигается ценой введения избыточности. Это означает, что если применяя для передачи информации код, у которого используются не все возможные комбинации, а только некоторые из них, можно повысить помехоустойчивость приёма. Такие коды называют избыточными или корректирующими.

Корректирующие свойства избыточных кодов зависят от правил построения этих кодов и параметров кода (длительности символов, числа разрядов,

избыточности и др.).

В настоящее время известно большое количество корректирующих кодов,

отличающихся как принципами построения, так и основными характеристиками. Рассмотрим их простейшую классификацию, дающую представление об основных группах, к которым принадлежит большая часть известных кодов.

Классификация корректирующих кодов

Все известные в настоящее время корректирующие коды могут быть разделены на две большие группы: блочные и непрерывные. Блочные коды

характеризуются тем, что последовательность передаваемых символов разделена на блоки. Операции кодирования и декодирования в каждом блоке производятся отдельно. Отличительной особенностью непрерывных кодов

154

является то, что первичная последовательность символов, несущих информацию, непрерывно преобразуется по определённому закону в другую последовательность, содержащую избыточное число символов. Здесь процессы кодирования и декодирования не требуют деления кодовых символов на блоки.

Разновидностями как блочных, так и непрерывных кодов являются разделимые и неразделимые коды. В разделимых кодах всегда можно выделить информационные символы, содержащие передаваемую информацию, и

контрольные (проверочные) символы, которые являются избыточными и служат исключительно для коррекции ошибок. В неразделимых кодах такое разделение провести невозможно.

Наиболее многочисленный класс разделимых кодов составляют линейные коды. Основная их особенность состоит в том, что контрольные символы образуются как линейные комбинации информационных символов. В свою очередь, линейные коды могут быть разбиты на два подкласса:

систематические и несистематические. Все двоичные систематические коды являются групповыми. Последние характеризуются принадлежностью кодовых комбинаций к группе, обладающей тем свойством, что сумма по модулю 2

любой пары комбинаций снова даёт комбинацию, принадлежащую к этой группе. Линейные коды, которые не могут быть отнесены к подклассу систематических, называются несистематическими.

Основными характеристиками корректирующих кодов являются избыточность кода, кодовое расстояние, число обнаруживаемых и исправляемых ошибок, корректирующие возможности кодов. Рассмотрим их.

Основные характеристики корректирующих кодов

Как уже неоднократно отмечалось, способность кода обнаруживать и исправлять ошибки обусловлена наличием избыточных символов. Пусть на ввод кодирующего устройства поступает последовательность из

P информационных двоичных символов, а на выходе ей соответствует последовательность из N двоичных символов, причем N > P. В этом случае

155

всего может быть 2Q различных входных последовательностей и 2				различных
выходных последовательностей. Из общего числа			2	выходных
последовательностей только 2Q последовательностей соответствуют входным.
Будем называть их		разрешёнными кодовыми комбинациями.		Остальные
2 − 2Q	возможных	выходных последовательностей	для передачи не

используются. Их будем называть запрещёнными кодовыми комбинациями.

Искажение информации в процессе передачи сводится к тому, что некоторые из передаточных символов заменяются другими – неверными.

Каждая из 2Q разрешённых комбинаций в результате действия помех может трансформироваться в любую другую. Всего может быть 2Q ∙ 2 возможных

∙2Q случаев безошибочной передачи;

∙2Q ∙ 2Q − 1 случаев перевода в другие разрешённые комбинации, что

соответствует необнаруживаемым ошибкам;

2Q ∙ 2 − 2Q случаев перехода в неразрешённые комбинации, которыеслучаев. В это число входит:

могут быть обнаружены.

Часть обнаруживаемых ошибочных кодовых комбинаций от общего числа возможных случаев передачи соответствует:

обн. =	2Q ∙ 2	= 1 − 2	(6.3)

В качестве примера рассчитаем обнаруживающую способность кода,

каждая комбинация которого содержит всего один избыточный символ, т.е.

N = P + 1. Общее число выходных последовательностей составит 2Qi , что вдвое больше общего числа кодируемых входных последовательностей. За подмножество разрешенных кодовых комбинаций можно принять, например,

подмножество 2Q комбинаций, содержащих четное число единиц (или нулей).

Тогда, при кодировании к каждой последовательности из P информационных символов добавляется один символ (0 или 1), – такой, чтобы число единиц в кодовой комбинации было чётным. Искажение любого чётного числа символов

156

переводит разрешенную кодовую комбинацию в подмножество запрещенных комбинаций, что обнаруживается на приемной стороне по нечётности числа единиц (см. выше коды с обнаружением ошибок раздел 6.2.1). Часть обнаруженных ошибок в этом случае составит >.

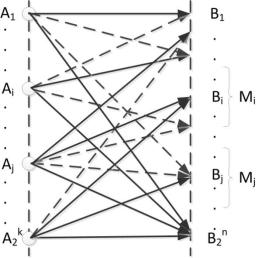
Рассмотрим случай исправления ошибок. Любой метод декодирования можно рассматривать как правило разбиения всего множества запрещённых кодовых комбинаций на 2Q непересекающихся подмножеств l , каждое из которых ставится в соответствие одной из разрешённых комбинаций. При получении запрещённой комбинации, принадлежащей подмножеству l ,

принимают решение, что передавалась разрешённая комбинация m (рис. 6.4).

Ошибка будет исправлена в тех случаях, когда полученная комбинация действительно образовалась из m , т.е. в 2 − 2Q случаях.

Рис. 6.4. Схематичное представление перехода передаваемых комбинаций в

разрешённые (сплошные стрелки) и неразрешённые (штриховые стрелки)

комбинации:

А – передаваемые комбинации; В – полученные комбинации; М – непересекающиеся

подмножества

Всего случаев перехода в неразрешённые комбинации 2Q ∙ 2 − 2Q .

Таким образом, при наличии избыточности любой код способен исправлять

157

ошибки. Отношение числа исправляемых кодом ошибочных кодовых комбинаций к числу обнаруживаемых ошибочных комбинаций равно:

2Q ∙ 2 − 2Q	= 2Q	(6.4)

Способ разбиения на подмножества зависит от того, какие ошибки должны исправляться данным конкретным кодом. Большинство разработанных до настоящего времени кодов предназначено для корректирования взаимно независимых ошибок определённой кратности и пакетов ошибок.

Взаимно независимыми ошибками будем называть такие искажения в передаваемой последовательности символов, при которых вероятность появления любой комбинации искажённых символов зависит только от числа искажённых символов ] и вероятности искажения одного символа .

Количество искажённых символов в кодовой комбинации называют

кратностью ошибки. При взаимно независимых ошибках вероятность искажения любых ] символов в n-разрядной кодовой комбинации может быть определена:

где – вероятность	S		(6.5)
	искажения одного символа; DS – число ошибок
порядка ]; n – количество разрядов кодовой комбинации.
Если учесть, что	1, то в этом случае наиболее вероятны ошибки

низшей кратности. Их следует обнаруживать и исправлять в первую очередь.

Таким образом, при взаимно независимых ошибках наиболее вероятен переход в кодовую комбинацию, отличающуюся от данной наименьшим числом символов.

Степень отличия любых двух кодовых комбинаций характеризуется так называемым кодовым расстоянием n., которое выражается числом символов, в

которых комбинации отличаются одна от другой. Чтобы получить кодовое расстояние между двумя комбинациями двоичного кода, достаточно

158

подсчитать число единиц в сумме этих комбинаций по модулю 2.

Пример.		*	*
			*	*	*,	n = 3
	*		*

Кодовое расстояние может быть различным. Так, в первичном натуральном безызбыточном коде это расстояние для различных комбинаций может различаться от единицы до N, равной разрядности кода.

Число обнаруживаемых ошибок определяется минимальным расстоянием между разрешёнными кодовыми комбинациями. Это расстояние называется

хэмминговым и определяется как минимальное расстояние, взятое по всем парам кодовых разрешённых комбинаций кода.

В безызбыточном коде все комбинации являются разрешёнными, т.е. n% = 1. Достаточно только исказиться одному символу, и будет ошибка в сообщении.

Чтобы код обладал свойствами обнаруживать одиночные ошибки,

необходимо ввести избыточность, которая обеспечивала бы минимальное расстояние между любыми двумя разрешёнными комбинациями было не менее двух.

Пример. Возьмем разрядность кода N = 3. Возможные комбинации натурального кода образуют следующее множество:

000, 001, 010, 011, 100, 101, 110, 111.

Любая одиночная ошибка трансформирует данную комбинацию в другую разрешённую комбинацию. Ошибки здесь не обнаруживаются и не исправляются, так как n% = 1.

Разобьём данный код на два подмножества. Пусть подмножество разрешённых комбинаций образовано по принципу четности числа единиц.

Тогда подмножества разрешённых и запрещённых комбинаций будут такие: 000, 011, 101, 110 – разрешённые комбинации;

159

001, 010, 100, 111 – запрещённые комбинации.

Минимальное расстояние между любыми двумя разрешёнными
комбинациями в данном случае			% = 2 и ни одна из разрешённых кодовых
комбинаций при одиночной	ошибке не переходит в другую разрешённую
		n

комбинацию, поскольку искажение помехой одного разряда (одиночная

ошибка) приводит к переходу комбинации в подмножество запрещённых комбинаций. Такой код обнаруживает все одиночные ошибки.

В общем случае при необходимости обнаруживать ошибки кратности ],

минимальное кодовое расстояние должно быть, по крайней мере, на единицу больше ], т.е. n% = ] + 1. В этом случае никакая ошибка кратности ] не в состоянии перевести одну разрешённую комбинацию в другую.

Для исправления одиночной ошибки каждой разрешённой кодовой комбинации необходимо сопоставить подмножество запрещённых кодовых комбинаций. Чтобы эти подмножества не пересекались, минимальное кодовое

расстояние должно быть не менее трёх.

Пример. Пусть, как и в предыдущем примере, N = 3. Примем разрешённые комбинации 000 и 111 (кодовое расстояние между ними n = 3).

Разрешённой комбинации 000 поставим в соответствие подмножество

запрещённых комбинаций 001, 010, 100. Эти запрещённые комбинации

образуются в результате возникновения единичной ошибки в комбинации 000.

Аналогично разрешённой комбинации 111 необходимо поставить в

соответствие подмножество запрещённых комбинаций 110, 011, 101. Если

сопоставить эти подмножества запрещённых комбинаций, то очевидно, что они
не пересекаются (рис. 6.5).				100
	r			001
		111		011v
Разрешённые комбинации	s000			010w	Запрещённые комбинации
	p			110u

Рис. 6.5. Подмножества разрешённых и запрещённых комбинаций

160