Методическое пособие Теория информации-2

следовательно, вероятность того, что при броске двух костей суммарное количество очков будет равно семи, составляет + + + + + = .

Введём математическое определение информации, основываясь на вероятностном подходе. Пусть имеет место передача сообщения от источника к приёмнику о том, что произошло некое событие. Тогда, количество информации, содержащейся в сообщении будет равно:

полученная информация

вероятность у приёмника данного события

= log после приёма сообщения (1.3)

вероятность у приёмника данного события до приёма сообщения

В случае отсутствия шумов (приёмник принимает информацию безошибочно) вероятность события после приёма информации о нём равна единице и предыдущее выражение принимает вид:

полученная информация в отсутствии шумов
= −log	вероятность у приёмника данного события		(1.4)
	до приёма сообщения

При определении количества информации наиболее часто используют двоичное, реже десятичное основание логарифма. Одна двоичная единица

(дв. ед.) информации соответствует сообщению о том, что произошло одно из двух равновероятных событий.

1.2. Экспоненциальный закон количества сообщений. Закон больших чисел

Пусть существует алфавит, содержащий символов. Тогда количество сообщений, представляющих собой последовательность из символов такого алфавита, можно определить по формуле:

количество сообщений	(1.5)
Пример. Пусть алфавит состоит из символов А, В и С. Количество
сообщений, представляющих собой последовательность из двух	символов
11

данного алфавита будет равно 3 = 9. Сами сообщения будут выглядеть, как:

АА АВ АС ВА ВВ ВС СА СВ СС

При расчёте количества возможных сообщений можно измерять длительность сообщения не количеством входящих в него символов , а во временных единицах. При этом, время, требуемое для передачи каждого из

символов, может различаться , , … , . В этом случае число возможных сообщений при условии, что длительность сообщения велика по сравнению со временем, требуемым для -кратной передачи самого длинного символа,

может быть рассчитано следующим образом:

количество сообщений							# ,	(1.6)
где ! и "# – константы, зависящие от количества символов								и от длительности
символов.
"# является наибольшим действительным корнем уравнения:
	Х&' + Х&( + + Х&* = 1							(1.7)
Если длительность всех символов одинакова и равна #, то уравнение
преобразуется к виду:
"#&+ = 1								(1.8)
"# = &+								(1.9)
В этом случае коэффициент ! = 1 и с учетом (1.6) имеем:
количество сообщений = &+							=	(1.10)

Кроме неравной длительности символов при построении кодов возможны

фиксированные ограничения, которые уменьшают количество различных возможных сообщений заданной длительности. Фиксированные ограничения имеют конечную длительность, т.е. при данных ограничениях некоторый символ или комбинация символов в последовательности ограничивают выбор лишь конечного числа последующих символов. В качестве примера

12

фиксированного ограничения можно привести телеграфный код, содержащий четыре символа: точка, тире, промежуток между буквами и промежуток между словами. Этот код построен таким образом, что вслед за любым промежутком должна обязательно следовать точка или тире.

Если на код наложены только фиксированные ограничения, то для последовательности большой длительности количество возможных сообщений будет определяться формулой:

где , и	количество сообщений	,	(1.11)
	– константы, зависящие от количества,		длительности символов и

характера фиксированных ограничений.

Таким образом, можно сделать вывод, что в общем случае возможное

число различных сообщений длительности с увеличением длительности

сообщения растёт по экспоненциальному закону.

Кроме фиксированных ограничений на коды могут налагаться вероятностные ограничения. Для их изучения требуется рассмотреть закон больших чисел.

Пример. Вероятности выпадения при подбрасывании монеты «герба»

(далее будем обозначать Г) или «решки» (далее будем обозначать Р) равны .

Подбрасывание монет являются событиями не зависимыми и, следовательно,

вероятность того, что все монеты упадут «гербом» вверх равняется произведению вероятностей и может быть определена как -. Вероятность выпадения одних «гербов» мала, но все-таки существует и значительно отличается от вероятности выпадения «герба» при подбрасывании одной монеты.

Рассмотрим два случая – одновременное подбрасывание четырёх и двадцати монет. Возможные комбинации (16 комбинаций) для случая с

четырьмя монетами приведены в табл. 1.1. Вероятность выпадения каждой из

∙ ∙ ∙ =

приведенных в табл. 1.2 16-ти комбинаций равна . В табл. 1.2

13

приведены данные о числе комбинаций, в которых выпало от 4 до 0 «гербов», а

также вероятность их появления.

Таблица 1.1

Возможные комбинации при подбрасывании четырёх монет

ГГГГ	ГРГГ	РГГГ	РРГГ
ГГГР	ГРГР	РГГР	РРГР
ГГРГ	ГРРГ	РГРГ	РРРГ
ГГРР	ГРРР	РГРР	РРРР

Таблица 1.2

Вероятность комбинаций с различным числом выпавших «гербов»

Число выпавших «гербов»	4	3	2	1	0
Количество возможных комбинаций	1	4	6	4	1
Вероятность выпадения данного	16	16	16	16	16
числа «гербов»

Из табл. 1.2 можно сделать вывод, что выпадение двух «гербов» и двух

«решек» более вероятно, чем выпадение любой другой комбинации.

Рассмотрим вариант с подбрасыванием 20 монет. В этом случае число возможных комбинаций будет равняться 2# = 1 048 576. Число комбинаций,

в которых выпадет 5Г «гербов» и 5Р «решек», можно рассчитать в соответствии с теорией сочетаний по формуле:

=	5 ! ∙ 5 !	(1.12)
	Г Р

Количество различных комбинаций , при которых выпадают от 0 до 20

«гербов» при подбрасывании 20 монет, и вероятность их выпадения представлены в табл. 1.3.

Анализ данных, приведенных в табл. 1.3 позволяет заметить, что приблизительно в 74 % всех возможных случаев при подбрасывании 20 монет

14

выпадает от 8 до 12 «гербов». Таким образом, в 74 % случаев количество выпавших «гербов» отличается от 10 не более чем на 20 %.

Таблица 1.3

Количество различных комбинаций n, при которых выпадают

от 0 до 20 «гербов» при подбрасывании 20 монет

		7 = :	Г89!		!	Вероятность
NГ	NР			Р		выпадения NГ
			! ∙ :			«гербов»
0	20		1			0.000001
1	19		20			0.000019
2	18		190			0.00018
3	17	1 140				0.0011
4	16	4 845				0.005
5	15	15 504				0.015
6	14	38 760				0.037
7	13	77 520				0.074
8	12	125 970				0.120
9	11	167 960				0.160
10	10	184 756				0.176
11	9	167 960				0.160
12	8	125 970				0.120
13	7	77 520				0.074
14	6	38 760				0.037
15	5	15 504				0.015
16	4	4 845				0.005
17	3	1 140				0.0011
18	2		190			0.00018
19	1		20			0.000019
20	0		1			0.000001
Итого:		1 048 576				1.000

Из приведенного примера с 4 и 20 монетами, наглядно видно, что при увеличении числа монет вероятность того, что приблизительно всех монет упадет «гербом» вверх, заметно возрастает. Сильно увеличивая число монет,

можно найти такое число их, при котором в 99.9(9) % случаев количество

15

выпавших «гербов» и «решек» будет отличаться от половины всех монет не более чем на 0.0001 %, т.е. вероятность выпадения «гербов» составит .

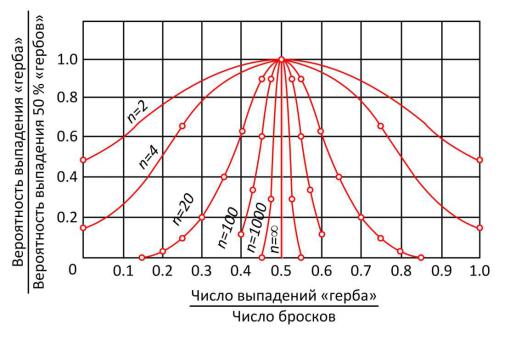
На рис. 1.2 показано, как изменяется вероятность выпадений «герба» с

увеличением количества подброшенных монет.

Рис. 1.2. Нормированный график, иллюстрирующий изменение вероятности

выпадений «герба» с увеличением числа испытаний

Пример. Пусть существуют последовательности из 20 символов, каждый из которых принимает значение «А» или «В». Вероятность появления в последовательности символа «А» равна ;, а символа «В» – ;. Появление любого из символов в последовательности никак не связано с появлением остальных символов.

Общее возможное число различных последовательностей как и в предыдущем примере будет равно 2# = 1 048 576. Вероятность появления той или иной последовательности будет зависеть от количества содержащихся в ней символов «А» (5 ), символов «В» (5 ) и может быть выражена через произведение вероятностей в соответствии с (1.13).

16

< = < => ∙ < =? = @;A > ∙ @;A ?.		(1.13)
В табл. 1.4 представлены данные о вероятности появления
последовательностей из 20 символов, содержащих	5	символов «А» и 5

символов «В», расположенных произвольно.

Таблица 1.4

Количество и вероятность появления различных последовательностей из

20 символов, включающих NA символов «А» и NB символов «В»,

расположенных произвольно

NА	NВ	А89! В	:C		:D	последовательности,
		7 = : ! ∙ : !	B = BC	∙ BD		Вероятность
						появления
						содержащей NА и NВ
0	20	1	9.095·10– 13			9.095·10– 13
1	19	20	2.728·10– 12			5.457·10– 11
2	18	190	8.185·10– 12			1.555·10– 9
3	17	1 140	2.456·10– 11			2.799·10– 8
4	16	4 845	7.367·10– 11			3.569·10– 7
5	15	15 504	2.210·10– 10			3.426·10– 6
6	14	38 760	6.630·10– 10			2.570·10– 5
7	13	77 520	1.989·10– 9			1.542·10– 4
8	12	125 970	5.967·10– 9			7.517·10– 4
9	11	167 960	1.790·10– 8			3.007·10– 3
10	10	184 756	5.370·10– 8			9.922·10– 3
11	9	167 960	1.611·10– 7			2.706·10– 2
12	8	125 970	4.833·10– 7			6.089·10– 2
13	7	77 520	1.450·10– 6			1.124·10– 1
14	6	38 760	4.350·10– 6			1.686·10– 1
15	5	15 504	1.305·10– 5			2.023·10– 1
16	4	4 845	3.915·10– 5			1.897·10– 1
17	3	1 140	1.175·10– 4			1.339·10– 1
18	2	190	3.524·10– 4			6.695·10– 2
19	1	20	1.057·10– 3			2.114·10– 2
20	0	1	3.171·10– 3			3.171·10– 3
Итого:		1 048 576				1.000
			17

Наибольшее значение имеет вероятность появления последовательностей,

содержащих 15 символов «А», что составляет ; от общего числа символов, и 5

символов «В», что составляет ; от общего числа символов. Если увеличивать

количество символов в последовательности, то вероятность появления

последовательностей, в которых будет содержаться почти точно ; символов

«А» и ; символов «В», будет быстро приближаться к единице.

Рассмотренные примеры являются частными случаями математического явления, называемого законом больших чисел. Это явление состоит в том, что в последовательности независимых испытаний, в каждом из которых с некоторой вероятностью может появиться некоторое событие, относительная частота появления события сколь угодно мало отклоняется от вероятности появления этого события с вероятностью, сколь угодно близкой к единице, если последовательность испытаний достаточно длинна.

Последовательность, в которой процентное содержание отдельных событий соответствует заданным вероятностям их появления, называют

типичной последовательностью для данного процесса. В последовательностях конечной длины истинное распределение событий обычно отклоняется от того,

которое задается вероятностями их появлений.

1.3. Коды с вероятностным ограничением. Языки

Передача информации между людьми происходит посредством того или иного языка. Одна из важнейших особенностей всех языков, отличающая их от искусственно построенных кодов, состоит в том, что возникающие в языках ограничения управляются вероятностными законами. Известно, что частота повторения определенных букв в каждом языке – величина постоянная и легко определяемая. Распределение букв очень сильно зависит от типа текста: проза,

разговорный язык, технический язык и т.д. В качестве примера в табл. 1.5

приведены данные о частоте повторения букв русского алфавита.

18

						Таблица 1.5
	Средняя частота повторения букв в русском языке
Буква	Частота	Буква	Частота	Буква		Частота
	повторения		повторения			повторения
а	0.062	л	0.035	ц		0.004
б	0.014	м	0.026	ч		0.012
в	0.038	н	0.053	ш		0.006
г	0.013	о	0.090	щ		0.003
д	0.025	п	0.023	ы		0.016
е, ё	0.072	р	0.040	ъ, ь		0.014
ж	0.007	с	0.045	э		0.003
з	0.016	т	0.053	ю		0.006
и	0.062	у	0.021	я		0.018
й	0.010	ф	0.002	разделитель		0.174
к	0.028	х	0.009

В целом, частоты букв и их сочетаний, частоты слов и их сочетаний и другие подобные характеристики, взятые вместе, описывают структуру языка.

При этом, различная вероятность появления тех или иных букв и их сочетаний уменьшает количество отличающихся друг от друга сообщений заданной длины. Это свойство языков очень ценно, так как оно повышает надёжность сообщений, снижает возможность их ложного толкования.

Сообщения, изложенные на том или ином языке, являются довольно близким приближением к эргодическим сообщениям. Эргодической называется такая система символов, в которой появление символов является случайным, а

заметное влияние предшествующих символов на последующие простирается только на такое их число, максимальное значение которого является конечным.

Согласно данному определению, в эргодическом сообщении взаимную связь между символами, отстоящими достаточно далеко друг от друга, можно рассматривать как случайную.

Для эргодических сообщений справедлив закон больших чисел.

Достаточно длинная последовательность, являющаяся отрывком эргодического

19

сообщения, характеризует вероятности отдельных символов и связи между символами, присущие самому эргодическому сообщению.

Число различающихся между собой последовательностей символов заданной длительности, на которые наложены вероятностные ограничения и которые удовлетворяют условиям эргодичности, растёт с увеличением длительности по экспоненциальному закону. Можно показать, что возможное число различающихся между собой эргодических последовательностей из E

символов F E равно:

	,	(1.14)
где ! – постоянная, не зависящая от длины последовательности; –		переменная
зависящая от вероятности появления	H– го элементарного сообщения (<I) и от

среднего количества символов в элементарном сообщении, характеризующаяся
переменной J:
= − J KI <I log <I	(1.15)
K <I log <I = < log < + < log < + + <I log <I + + < log < ,	(1.16)
I
где – общее число элементарных сообщений.

Выражение (1.14) справедливо для эргодической последовательности,

которая может быть разложена на отдельные группы символов – элементарные сообщения. Величина J больше, чем наибольшее расстояние, на котором ещё

проявляются взаимные связи между символами.

Если оперировать не длиной сообщения, а их длительностью, то возможное количество эргодических сообщений F длительности

составит:

F = ! ∙ 2M ,	(1.17)
где N – средняя длительность элементарных сообщений.
Выражение (1.17) справедливо только при достаточно больших значениях
. Данный закон аналогичен закону (1.11).
20