Методическое пособие Теория информации-2

Первый способ организации частотной манипуляции – когда все посылки,

соответствующие одному закону передаваемого символа, имеют одинаковую начальную фазу, то есть являются идентичными. При этом можно заранее сформировать наборы отсчётов для всех возможных дискретных символов.

Тогда осуществление частотной манипуляции сводится к последовательной передаче заранее рассчитанных последовательностей отсчётов,

соответствующих поступающим символам. Однако если используемые частоты манипуляции не кратны символьной скорости, сформированный таким образом ЧМн– сигнал будет содержать разрывы (скачки) на стыках символов.

Вследствие этого спектр сигнала будет иметь всплески на частотах, кратных символьной скорости.

Второй способ организации частотной манипуляции – непрерывная генерация колебаний всех необходимых частот и осуществление переключения между этими сигналами в соответствии с поступающими символами. Данный способ также не гарантирует отсутствие скачков на стыках символов, но вследствие того, что начальные фазы посылок меняются от символа к символу,

скачки возникают не на всех стыках и их величина оказывается различной. В

результате возникающие из-за скачков всплески спектра в данном случае выражены слабее.

Третий способ организации частотной манипуляции – когда поступающие для передачи символы управляют скоростью линейного нарастания текущей фазы, а частотно-манипулированный сигнал формируется путём вычисления косинуса этой текущей фазы. При этом фазовая функция (а

значит, и сам ЧМн-сигнал) оказывается непрерывной (не имеющей скачков).

Данный способ сложнее в реализации, но он даёт наиболее компактный спектр сигнала. ЧМн-сигнал, полученный таким образом, называется частотно– манипулированным сигналом с непрерывной фазовой функцией.

Для повышения помехоустойчивости ЧМн желательно, чтобы посылки,

соответствующие разным символам, были некоррелированы, т.е. имели

131

нулевую взаимную корреляцию. Минимальное значение расстояния между соседними частотами манипуляции, при котором посылки, соответствующие разным символам, оказываются некоррелированными, составляет половину символьной скорости:

				SI							(5.21)
			∆²SI =			=					(5.22)
	²$				2			2
где		– символьная скорость.
		Двухпозиционная (двоичная) ЧМн, частоты которой выбраны согласно
(5.21) и (5.22), получила название минимальной частотной манипуляции.
		При квадратурной манипуляции каждому из возможных значений
дискретного символа			ставится в соответствие пара величин – амплитуды

синфазной и квадратурной составляющих либо (что эквивалентно) амплитуда и
•µ
начальная фаза несущего колебания:
µ	µ	#	µ	#	(5.23)
					(5.24)
µ		µ	#

Параметры• аналогового колебания, сопоставленные дискретному символу(, µ+, удобноmN ) представлять в виде комплексного числа в алгебраической форме µ µ . Совокупность этих комплексных чисел для всех возможных значений дискретного символа называется сигнальным созвездием.

Стоит отметить, что кроме рассмотренных в данном разделе видов модуляции существуют и ряд других, основанных на их комбинациях.

132

6. Кодирование информации для передачи сообщения по каналу

связи

Как уже отмечалось ранее (раздел 4), для передачи сообщения по каналу связи его необходимо представить в форме, пригодной для передачи по данному каналу, т.е. провести кодирование сообщения. Термин «кодирование» можно определить, как операцию идентификации символов или групп символов некоторого кода с символами или группами символов другого кода.

Существует ряд задач, решаемых при помощи кодирования:

1.Преобразование дискретных сообщений из одних систем счисления в другие (из десятичной в двоичную, восьмеричную и т.п., из непозиционной в позиционную, преобразование буквенного алфавита в цифровой и т.д.).

2.Кодирование сообщений может производиться с целью сокращения объёма информации и повышения скорости её передачи или сокращения полосы частот, требуемых для передачи. Такое кодирование называют экономным, безызбыточным, или эффективным кодированием, а также сжатием данных.

3.Кодирование в канале, или помехоустойчивое кодирование информации может быть использовано для уменьшения количества ошибок, возникающих при передаче по каналу с помехами.

4.Кодирование с целью засекречивания передаваемой информации. При этом элементарным сообщениям из начального алфавита ставятся в соответствие последовательности цифр или букв из специальных кодовых таблиц, известных лишь отправителю и получателю информации.

Основание кода может быть любым – двоичным, четверичным,

восьмеричным, десятичным и т.д., однако наибольшее распространение получили двоичные коды. В данном разделе будут рассмотрены методы кодирования информации при ее передаче по дискретному каналу без помех, а

так же методы построения корректирующих кодов для передачи информации по каналу связи с помехами.

133

6.1. Кодирование информации при передаче по дискретному каналу

без помех

6.1.1. Общие принципы построения кодов. Кодовые таблицы и кодовые

деревья. Равномерные и неравномерные коды

Самым простым способом представления или задания кодов являются кодовые таблицы, ставящие в соответствие сообщениям соответствующие им коды (табл. 6.1).

			Таблица 6.1
	Пример кодовой таблицы
Кодируемый	Код с основанием 10	Код с основанием 4	Код с основанием 2
символ
А	0	00	000
Б	1	01	001
В	2	02	010
Г	3	03	011
Д	4	10	100
Е	5	11	101
Ж	6	12	110
З	7	13	111

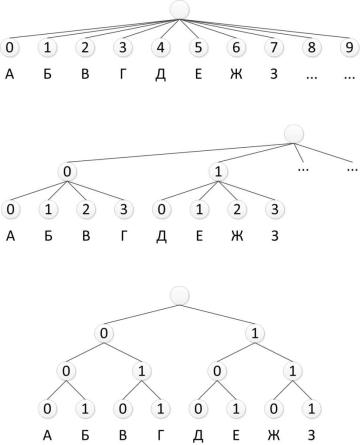
Другим наглядным и удобным способом описания кодов является их представление в виде кодового дерева (рис. 6.1).

Для того чтобы построить кодовое дерево для данного кода, начиная с некоторой точки – корня кодового дерева, проводятся ветви (0 или 1). На вершинах кодового дерева находятся буквы алфавита источника, причём каждой букве соответствуют своя вершина и свой путь от корня к вершине. К

примеру, букве А соответствует код 000, букве В – 010, букве Е – 101 и т.д. (рис. 6.1в).

Код, полученный с использованием кодового дерева, изображённого на рис. 6.1в, является равномерным трёхразрядным кодом. Равномерные коды очень широко используются в силу своей простоты и удобства процедур кодирования-декодирования: каждой букве соответствует одинаковое число бит; декодирование производится после принятия определённого числа бит

134

путём поиска соответствия кодовой таблице.

а

б

в

Рис. 6.1. Кодовые деревья к табл. 6.1:

а – код с основанием 10; б – код с основанием 4; в – код с основанием 2

Наряду с равномерными кодами могут применяться и неравномерные коды, когда каждая буква из алфавита источника кодируется различным числом символов. Неравномерные коды подразделяют на приводимые (или непрефиксные) и префиксные.

Приводимые коды не обеспечивают однозначного декодирования и не могут на практике применяться без специальных разделяющих символов. В

качестве примера такого кода можно привести: А – 1; Б – 0;

В – 11; Г – 10; Д – 01; Е – 00. В этом случае нельзя однозначно декодировать сообщение АББА – 1001, поскольку точно такой же код будут иметь сообщения ГД и АЕА.

Префиксные коды относятся к неравномерным кодам, которые допускают

135

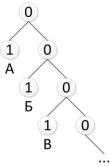
однозначное декодирование. Для построения таких кодов необходимо, чтобы всем буквам алфавита соответствовали лишь вершины кодового дерева,

например, такого, как показано на рис. 6.2. Здесь ни одна кодовая комбинация не является началом другой, более длинной, поэтому неоднозначности декодирования не будет.

Рис. 6.2. Пример кодового дерева префиксного кода

Приём и декодирование неравномерных кодов – процедура гораздо более сложная: усложняется аппаратура декодирования и синхронизации, поскольку поступление элементов сообщения (например, отдельных символов) становится нерегулярным. Так, при приёме сообщений, декодированных при помощи кодового дерева, изображенного на рис. 6.2, приняв первый 0, декодер ищет соответствие некоему символу в кодовой таблице. Поскольку соответствия с каким-либо символов в данном случае нет, то происходит ожидание поступления следующего символа. Если следующим символом будет 1, тогда декодирование первой буквы завершится – это будет Б; если же вторым принятым символом снова будет 0, то декодер будет ожидать поступления третьего символа и т.д.

Несмотря на указанные недостатки, неравномерные коды дают преимущество при кодировании не равновероятных сообщений. Рассмотрим пример, иллюстрирующий данное преимущество.

Пример. Пусть производится кодирование сообщений из алфавита объёмом = 8 с помощью произвольного -разрядного двоичного кода.

Вначале рассмотрим источник сообщения, который выдаёт некоторый

136

текст с алфавитом от А до З и одинаковой вероятностью букв = 1/8.

Кодирующее устройство кодирует эти буквы равномерным трёхразрядным кодом, приведенным в табл. 6.1. Определим основные информационные характеристики источника с таким алфавитом.

Энтропия источника равна:

	= −	log = 3 символ. .
			дв ед
Избыточность источника равна:
Избыточность кода:
	1 − log = 0
	1 −	= 0,

где = 3 – среднее число символов в коде.

Таким образом, при кодировании сообщений с равновероятными буквами

избыточность выбранного (равномерного) кода будет равна нулю.

Пусть теперь вероятности появления символов в сообщении будут

разными:
Символ:	А	Б	В	Г		Д	Е	Ж	З
Вероятность:	0.6	0.2	0.1	0.04	0.025 0.015			0.01	0.01
						дв ед
Энтропия источника составит				= 1.78		символ. .	, а избыточность кода

при том же равномерном трехразрядном кодировании будет равна 0.41, что соответствует тому, что в среднем 4 символа из 10 не несут никакой информации.

В связи с тем, что при кодировании не равновероятных сообщений равномерные коды обладают большой избыточностью, было предложено использовать неравномерные коды, длительность кодовых комбинаций которых была бы согласована с вероятностью выпадения различных букв.

137

Такое кодирование называется статистическим.

Неравномерный код при статистическом кодировании выбирают так,

чтобы более вероятные буквы передавались с помощью более коротких комбинаций кода, а менее вероятные – с помощью более длинных. В результате уменьшается средняя длина кодовой группы в сравнении с использованием равномерного кодирования.

Операция кодирования тем более эффективна (экономична), чем меньшей длины кодовые слова сопоставляются сообщениям. Поэтому за характеристику эффективности статистических неравномерных кодов принимают среднюю длину кодового слова, определяемую следующим образом:

= = μ			(6.1)
где – вклад сообщения	в среднюю длину кодового слова; μ – длина
кодового слова, сопоставляемая	сообщению ;		– вероятность появления
сообщения .
Рассмотрим два известных способа		построения статистических
кодов – это методики Шеннона-Фано и Хаффмана.
6.1.2. Методика построения статистического кода Шеннона-Фано
Для построения этого кода все сообщения			выписываются в порядке

убывания их вероятностей. Записанные таким образом сообщения затем разбиваются на две по возможности равновероятностные подгруппы. Всем сообщениям первой подгруппы присваивают цифру 1 в качестве первого кодового символа, а сообщениям второй подгруппы – цифру 0. Аналогичное деление на подгруппы продолжается до тех пор, пока в каждую подгруппу не попадает по одному сообщению. Пример построения кода по методике Шеннона-Фано представлен в табл. 6.2.

Энтропия найденного кода равна = 2.75 дв.ед. ; средняя длина

символ

138

кодового		слова	–	= 2.84.							При			этом			среднее		число	нулей
# 0 = ∑		%'&	= 1.29, а вероятность их появления 0 = ) +*																= 0.455.
																			Таблица 6.2
			Пример построения кода Шеннона-Фано
																			Вклад	в
Сообщение		Вероятность			Разбиение												Длина		среднюю
		,		сообщения на										Код				-	слова
		сообщения															кодового		длину
					подгруппы												слова		кодового
/		0.35		1		1						1	1				2		0.70.
		0.15		1		0						1	0				2		0.30
0
		0.13		0		1	1					0	1	1			3		0.39
1
		0.09		0		1	0					0	1	0			3		0.27
2
		0.09		0		0	1	1				0	0	1	1		4		0.36
3
		0.08		0		0	1	0				0	0	1	0		4		0.32
4
		0.05		0		0	0	1				0	0	0	1		4		0.20
5
		0.04		0		0	0	0		1		0	0	0	0	1	5		0.20
7		0.02		0		0	0	0		0		0	0	0	0	0	5		0.10
6

Аналогично среднее число единиц равно 1.55, а вероятность их появления – 0.545. Таким образом, полученный код близок к оптимальному.

Методика Шеннона-Фано не всегда приводит к однозначному построению кода. Ведь при разбиении на подгруппы можно сделать большей по вероятности как верхнюю, так и нижнюю подгруппы. От этого недостатка свободна методика Хаффмана.

6.1.3. Код Хаффмана

Для получения кода Хаффмана все сообщения выписывают в порядке убывания вероятностей. Две наименьшие вероятности объединяют скобкой и одной из них присваивают символ 1, а другой – 0. Затем эти вероятности складывают, результат записывают в промежутке между ближайшими вероятностями. Процесс объединения двух сообщений с наименьшими вероятностями продолжают до тех пор, пока суммарная вероятность двух оставшихся сообщений не станет равной единице. Код для каждого сообщения

139

строится при записи двоичного числа справа налево путём обхода по линиям вверх направо, начиная с вероятности сообщения, для которого строится код.

Пример построения кода Хаффмана приведен в табл. 6.3.

											Таблица 6.3
		Пример построения кода Хаффмана
Сообщение	Вероятность
					Объединение сообщений							Код
	сообщения
	0.35		0.35	0.35		0.35	0.35	0.35		0.37	0.63	11
/	,					0.17	0.20	0.28				101
	0.15		0.15	0.15						0.35	0.37
0	0.13		0.13	0.13		0.15	0.17	0.20		0.28		100
1	0.09		0.09	0.11		0.13	0.15	0.17				010
2	0.09		0.09	0.09		0.11	0.13					001
3	0.08		0.08	0.09		0.09						000
4	0.05		0.06	0.08								0110
5	0.04		0.05									01111
7	0.02											01110
6

Для лучшего понимания поясним кодирование , 8 и 9 сообщений.

Вероятность 9 = 0.02 . Это одна из двух складываемых наименьших вероятностей. Присваиваем коду значение 0, т.к. 9 < ; , а суммарная вероятность становится равной 0.06. Вероятность 0.6 входит в следующую сумму, однако, теперь из двух суммируемых вероятностей она наибольшая,

поэтому присваиваем коду справа налево единицу, получая 10. После суммирования вероятность пары становится равной 0.11 и участвует в суммировании через один столбец, причём из пары она наибольшая. В связи с этим присваиваем коду ещё одну единицу, получая 110. Суммарная вероятность данной пары равняется 0.20 и участвует в суммировании через один столбец, причём из пары она наибольшая. В связи с этим присваиваем коду ещё одну единицу, получая 1110. Суммарная вероятность данной пары равняется 0.37 и участвует в последнем суммировании через один столбец,

причём из пары она наименьшая. В связи с этим присваиваем коду ноль,

получая итоговый код 01110.

140