Математика Сизов 2011

r				5		co s			4						1 r					2		d rd						co s											2				4 r				3	2 r					5		1		r		7	1 r						2		d rd
S 2																															S 2																								4
		•				2			cos4 d													2 1 cos 2 2																						1 2						2cos 2								1 cos 4															•
																												2										d						4			1													2					d
							0															0																							0
																									1			3		sin 2														1								2			3	,
																									4			2																8	sin 4							0			4
																			остальные														интегралы															решены								ранее.
						•																																																																		•
			200											8					3						100												220																50			100					2						220
								5																							5																			5
				21							105								4							63											315																7				63				35
																																																																			315
			550					5			202
				63							315							.
x2 z2 x2dS2 x4dxdy																																							x r cos , r 2,0 2 ,
																																												z			0, dxdy rdrd
S2																						S2
																																													2										2										r6						2
																																																													3
r4 cos4 rdrd r5 cos4 drd cos4 d r5dr																																																																								8 .
		S2																						S2																					0										0						4					6					0
I						550				5					202								8								550							5			2722
	y																																															88,43 ед. момента инерции.
						63									315																63											315
I z							x2 y2										x2 dS x2 y2																							x2 dS1 x2 y2 x2 dS2 .
						S																				S1																								S2
x2 y2 x2dS1																					x2									y2 x2												1 x2								y2 dxdy
S1																								S2
						переход												к					полярным																	r2r2 cos2																1 r2 rdrd
										координатам																																S2
		2												2
																																	200												8
cos							2	d r									5								2
																				1 r						dr														5										.
																																		21											105
		0												0
x2 y2 x2dS2																			x2									y2 x2dxdy r2r2 cos2 rdrd
S2																						S2																								S2
	2										2														r	6		2				32
		cos2 d r 5 d																																			.
																												0					3
		0									0														6
I				200											8								32							200										1112
									5																										5											100,123									ед. момента инерции.
z						21																		3						21										105
												105

212

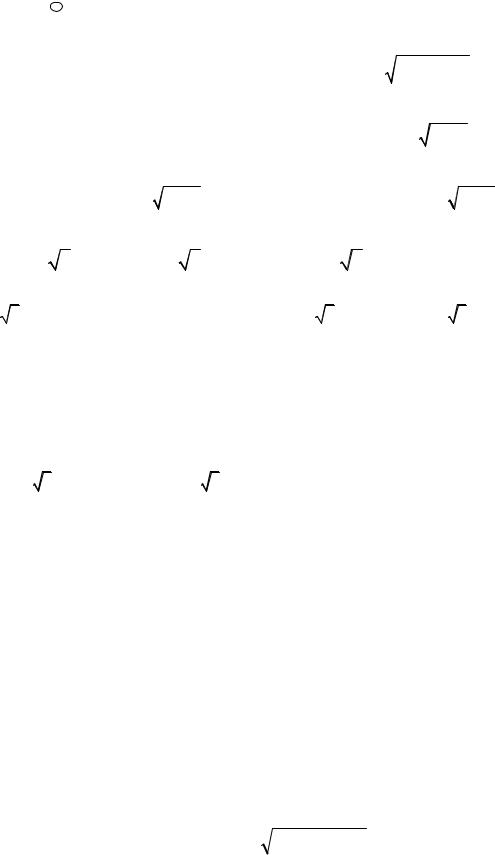
Io x2 y2 z2 x2dS x2 y2 z2 x2dS1 x2 y2 z2 x2dS2

									S																												S1																									S2
	2			y			2	z				2				2													2	y						2						2				1				2		y			2		2					2					2					2	dxdy
x													x dS1 x																																	2		x								x									1 x					y
S																						S
1																							2
			переход										к				полярным																										2					2				1	r	2		2				2					2			1 r				2	rdrd
							координатам																															r														2						r			cos
																																						S
					3				5				1			7				2														2				2					2					2						2					3					5		1			7						2
			4r			r								r											1 r																																4r			r							r				1		r			dr
													4			cos																			drd cos															d																4
S																																											0											0
2
				10												2							200															8									1				1840											16
		4								5																							5																									5
						3																	21															105									4					63										315
														15
						40					200						460							8										8								4							700									196								100								28
				5																																																		5																	5						.
						3						21					63							15							105									315										63								315										9						45
x				y			z					x dS2 x y																							x dxdy r cos rdrd r cos drd
	2					2				2 2														2										2				2											4				2														5				2
S2																			S2																											S2																			S2
2										2													6				2							32 .
cos2 d r5dr r
0										0											6						0							3
			100				5					28							32							100										5					508																	ед. момента инерции.
I0				9								45							3											9												45			113,46

14.1.5. Задание на контрольную работу

Вычислить массу, координаты центра масс и моменты инерции относительно координатных осей и начала координат материальной оболочки, которая представляет собой полую тонкостенную конструкцию, выполненную из композитного материала с

поверхностной плотностью		x, y, z	кг	. Оболочка имеет вид тела,
			3
		м
ограниченного поверхностями S1, S2, S3.
1.	x, y, z x2 y2 , S1 : z x2 y2 1, S2 : z 5 .
2.	x, y, z z2 ,	S1 : y 2 z 2 x2 ,			S2 : x 2.
3.	x, y, z x2 y2 , S : x2 y2			4z2 , S		2	: z 1, z 0.
		1
4.	x, y, z x2 y 2 , S1 : z 16 x2 y 2 , S2 : z 0.

5.x, y, z x2 y2 , S1 : 4 x2 y2 1 z 0, S2 : z 0.

6.x, y, z x2, S1 : x2 y2 z 1, S2 : z 0.

213

7.	x, y, z y2	, S : x2	z 2	1 y2 , S	2	: y 3, y > 0.
		1		9

8.x, y, z z, S1 : z 14 x2 y2 , S2 : z 1.

9.x, y, z y2 , S1 :1 z x2 y2 , S2 : z 0.

10.x, y, z z2 , S1 : x2 y2 4, S2 : z 2, S3 : z 2.

14.2. Поверхностный интеграл II рода

14.2.1. Определение

Поверхностный интеграл II рода от векторной функции (поля)

F x, y, z

по

ограниченному

куску

гладкой

двухсторонней

поверхности называется предел интегральной суммы:

lim

n

F x

, y

, z

i

ni S

i

F x, y, z ndS

i

,

где

n

i

i

max S 0 i 1

F(x, y, z) Fx (x, y, z)i Fy (x, y, z) j Fz (x, y, z)k – непрерывная

векторная

функция (поле) определённая

на

ограниченном

куске

гладкой двухсторонней поверхности σ (рисунок 14.4),

F

zy dydz

Si

–

площадь

i-ой

z

ni

элементарной

площадки, на

которые

разбит весь

кусок

поверхности

σ,

( i 1, n ).

xz dzdx

Si

Элемент

Si,

как бесконечно

малый

участок

кривой

поверхности σ, можно с

y

точностью до малых высшего

xy dy dx

порядка считать плоским,

x

n – количество элементарных

площадок,

Рис. 14.4.

F xi , yi , zi

–

значение

функции F в точке (xi,yi,zi), принадлежащей элементарной площадке

Si,

ni – единичный нормальный вектор к поверхности σ в точке (xi,yi,zi). Скалярное произведение векторов F xi , yi , zi ni есть высота

цилиндра с основанием Si			(рис. 14.4),
		xi , yi , zi ni Si	– объём указанного цилиндра.
	F

214

Если		x, y, z	– скорость			жидкости, протекающей через
	F
поверхность σ, то					xi , yi , zi	ni Si – количество жидкости,
				F

протекающей через элементарную площадку Si в единицу времени

м3

с или расход жидкости, ещё проще – поток жидкости. Тогда

интегральная сумма – приближенное значение, а её предел – точное

значение потока вектора F через всю поверхность.

Физический смысл поверхностного интеграла II рода – это есть количество жидкости, протекающей в единицу времени (расход, поток) через поверхность σ в направлении вектора n . Поэтому поверхностный интеграл II рода называют потоком векторного поля F через поверхность σ.

П F ndS.

Электротехнический смысл поверхностного интеграла II рода :

	если		плотность	А		электрического тока	i A , то
		J
				2
				м

i J ndS

есть ток, протекающий через сечение проводника с поверхностью . Скалярное произведение векторов F n образует скалярную

функцию f (x, y, z) и тогда поверхностный интеграл II рода преобразуется в поверхностный интеграл I рода.

14.2.2. Вычисление поверхностного интеграла II рода

При определении потока вектора F через поверхность σ как правило задают: вектор F , поверхность σ (уравнение) и сторону двухсторонней поверхности σ, через которую проходит поток. Последнее условие обычно кратко формулируется направлением единичного нормального вектора n к внутренней или внешней стороне поверхности σ: нормаль внутренняя или внешняя. От этого условия зависит знак потока вектора F , что отличает поверхностный интеграл II рода от поверхностного интеграла I рода.

Расчёт потока вектора сводится к вычислению двойного интеграла.

Пусть векторное поле F Fx x, y, z i Fy (x, y, z) j Fz (x, y, z)k. Поверхность σ задана уравнением z g x, y или x, y,z z g x, y 0.

Требуется найти поток П вектора F через поверхность σ, нормаль внешняя (внутренняя).

215

Воспользуемся формулами (14.1), приведёнными в 14.1.2, для единичного нормального вектора n к поверхности σ:

n grad cos i cos j cos k , grad

а также формулами (14.2,14.4,14.6),устанавливающие связь направляющих косинусов cosα, cosβ, cosγ вектора n с элементами интегрирования dx, dy, dz, dS:

dxdy cos dS , dydz cos dS , dxdz cos dS . (14.8)

Тогда поток П вектора F равен:

П Fnds

Fx (x, y, z)i Fy x, y, z j Fz x, y, z k cos i cos j cos k dS

Fx x, y, z cos dS Fj x, y, z cos dS Fz x, y, z cos dS

Fx x, y, z dydz Fy x, y, z dxdz Fz x, y, z dxdy.

По последнему виду интеграла поток вектора ещё называют поверхностным интегралом по координатам.

При расчёте потока вектора эту формулу нужно понимать так:

П F nds

Fx

yz

		y			z	(14.9)
x, y, z dydz		F	x, y, z dxdz		F	x, y, z dxdy .
	xz			xy

Здесь σyz, σxz, σxy есть проекции поверхности σ на соответствующие координатные плоскости (рисунок 14.4). Обязательным условием применения формулы (14.9) для расчёта потока вектора является однозначность проектирования поверхности σ на координатные плоскости.

Если это условие нарушается, нужно поверхность σ разделить на куски σ1, σ2,…σm, удовлетворяющие этому условию и расчёт потока вектора производить по каждому из этих кусков поверхности, а затем суммировать (см. раздел10, свойство 3).

Например, для расчёта потока вектора через поверхность S1 (рисунок 14.3) по формуле (14.9) нужно данную поверхность разделить на 4 части (по октантам) и в каждой из них вычислить три двойных интеграла, т.е. требуется вычислить всего 12 интегралов. При этом необходимо правильно выбрать знак + или – перед интегралом.

216

Ниже приводится формула, позволяющая, например, для данного случая (рисунок 14.3) рассчитать поток вектора только по одному двойному интегралу.

Перепишем формулы (14.8) в следующем виде:

dS dydz	, dS	dxdz	, dS dxdy	,	(14.10)
cos		cos	cos

Подставим формулы (14.10) в общую формулу для потока вектора:

dydz

F n

.

cos

yz

dxdz

F ndS

F n

(14.11)

cos

xz

dxdy

F

n

.

cos

xy

Для расчета потока вектора нужно выбрать любую из формул, удовлетворяющую условию однозначности проектирования поверхности σ на любую из координатных плоскостей.

Замечание. Элемент интегрирования dS есть площадь бесконечно-малой элементарной площадки, которая всегда положительная. Чтобы сохранить это обстоятельство в расчётной формуле при замене dS на соответствующие элементы интегрирования dx, dy, dz (положительные бесконечно-малые длины) и направляющие косинусы cosα, cosβ, cosγ по формулам (14.10), данные косинусы должны быть взяты по модулю.

Правила расчёта потока вектора

По условиям задачи построить чертёж (рисунок) поверхности σ и по нему определить координатную плоскость, на которую поверхность σ проектируется однозначно. Этим самым выбирается одна из трёх формул (14.11) и область интегрирования сформированного в дальнейшем двойного интеграла.

Если поверхность σ однозначно проектируется на несколько координатных плоскостей, то от выбора одной из них может зависеть эффективность (простота) расчёта. Иногда могут встретиться случаи, когда неудачный выбор координатной плоскости приводит к неберущемуся интегралу, а удачный выбор разрешает все проблемы.

По заданному уравнению поверхности σ найти единичный, нормальный вектор n к этой поверхности по формуле (14.1).

Здесь же определяются конкретные значения для направляющих косинусов, которые могут быть как числами, так и аналитическими выражениями (формулами).

217

Определить знак + или – для единичного, нормального вектора n , найденного по формуле (14.1). Для чего:

По условию задачи (нормаль внешняя или внутренняя) на рисунке построить вектор n ;

По рисунку определить знак того направляющего косинуса, который находится в выбранной формуле (14.1). Угол (α, β или γ) этого косинуса будет острым или тупым и сохраняться при перемещении вектора n по всей поверхности σ, а значит и знак этого косинуса будет сохраняться по всей этой поверхности;

Выбрать знак + или – перед аналитическим выражением вектора n (14.1) таким, чтобы знак направляющего косинуса, определённого в предыдущем пункте, совпадал со знаком этого косинуса в формуле для n .

Подставить значения F и n в формулу (14.11), произвести скалярное перемножение этих векторов, привести интеграл к двойному интегралу и рассчитать его. Если в подынтегральном выражении встречается переменная, не участвующая в интегрировании, то её нужно выразить через переменные интегрирования, используя уравнение поверхности σ. При необходимости двойной интеграл можно вычислить в полярной системе координат.

14.2.3. Некоторые приложения поверхностного интеграла II рода

Поверхностный интеграл II рода непосредственно применяется для вычисления потока вектора и электрического тока, о чём говорилось в 14.2.1. В тоже время, в формулах Остроградского-Гаусса и Стокса он нашёл применение, как в самом анализе, так и в его приложениях, в частности, в теории поля.

Формула Остроградского

Для векторной функции F Fx x, y, z i Fy (x, y, z) j Fz (x, y, z)k непрерывной вместе с частными производными первого порядка от координатных функций в пространственной области V, ограниченной замкнутой поверхностью S, имеет место следующая формула:

dF			dFy		dF
	x				z	dxdydz Fx dydz Fy dxdz Fz dxdz , или
V	dx		dy		dz		S

dF

dFy

dF

divFdV F ndS,

где divF

x

z .

dy

V

S

dx

dz

218

Интеграл от дивергенции векторного поля F по некоторому объёму равен потоку вектора через замкнутую поверхность, ограничивающую данный объём.

Формула Стокса

Для векторной функции F x, y, z Fx (x, y, z)i Fy (x, y, z) j Fz (x, y, z)k

непрерывной вместе с частными производными первого порядка от координатных функции в пространственной области V, содержащей гладкую поверхность σ, ограниченную контуром γ имеет место следующая формула:

dF

dFy

dF

dF

dFy

dF

Fx dx Fy dy Fz dz

dydz

x

dxdz

x

dxdy

z

z

dy

dz

dz

dx

dx

dy

или

rot

F

dl

F

ndS ,

						i				j
					d				d
		rot
	где		F
					dx				dy
					Fx				Fy

k d

dz Fz

dF

zdy

	dFy			dF
					x
	dz	i			dz

	dF			dFy
	z
	dx	j			dx

dF

x k dy

Циркуляция вектора F вдоль контура равна потоку ротора этого вектора через поверхность, натянутую на этот контур.

14.2.4. Типовые примеры решения поверхностных интегралов II рода

Пример 1. Вычислить поток векторного поля F через кривую поверхность тела V, заданного ограничивающими его поверхностями, нормаль внешняя.

F 3xi 2y j zk ,

V : x2 z2 y2 , y 1, y 4 .

Решение. Кривая поверхность тела V (рисунок 14.5) есть боковая поверхность усечённого конуса σ. Она однозначно проектируется на плоскость y = 0 в виде кольца. По формуле (14.11) определяем расчётную формулу:

	П		n			dxdz			.
		F
Рисунок 14.5.						cos
	xz

По формуле (14.1) определяем единичный нормальный вектор n к поверхности σ:

219

x2 z2

y2, y x2

z2 , y

x2 z2 0,

d i d

d

grad

j

k

dx

dy

dz

2x

i

2z

,

x2

1

z2

2 x2

z2

2.

j

k

grad

2 x2 z2

2 x2 z2

x2 z2

x2 z2

x2 z2

grad

x

1

z

i

.

n

j

k

grad

2 x

2

2

2

2 x

2

2

z

z

Выбираем знак «-» для вектора n . В формуле (14.11) для данного случая стоит cosβ. В формуле (14.1) он имеет конкретное

	значение: cosβ=	1	со знаком «+» . Но на рисунке 14.5 вектор n и
		2

ось Oy составляют тупой угол, значит cosβ отрицательный. Чтобы

привести cosβ в формуле (14.1) в соответствие с рис.14.5, вектор n нужно взять со знаком «-».

Окончательно:

x

i

1

z

.

n

j

k

2 x2 z2

2

2 x2 z2

Формируем расчётный интеграл.

П

ndS

n

dxdz

F

F

cos

xz

x

1

z

dxdz

3xi 2 y j zk

i

j

k

2 x

2

2

2

2 x

2

2

1

z

z

xz

2

3x2

z2

3x2

2

2

z2

2y

dxdz

2 x

z

dxdz

2

2

2

z

2

2

z

2

2

z

2

xz

x

z

2 x

x

xz

x

x

3x

2

2

z

2

z

2

5x

2

3z

2

dxdz

x

2

z

2

dxdz

x

2

z

2

xz

xz

=∙│∙ xz есть кольцо: внутренняя окружность r1 = 1, внешняя

окружность r2= 4. Перейдём к полярным координатам: x = rcosφ, z = rsinφ, 0≤φ≤2π, 1≤r≤4, dxdy = rdrdφ .|˙ =

	2		4	5r2 cos2 3r2 sin2								2		4	r2 2cos2 3
d										rdr d														rdr
				r2 cos2 r2 sin2														r
	0		1									0		1
	2		2cos2 3 d		4 r2dr				2	21 cos 2					3 d				r3				4
												2					3
	0				1				0														1
	2				64		1			63			1					2
												4		sin 2						168 .
			4 cos 2 d		3		3			3			2					0
	0

220

Пример 2. Даны векторное поле F и плоскость p, которая совместно с координатными плоскостями образует пирамиду V. Пусть σ – основание пирамиды, принадлежащее плоскости p, λ – контур ограничивающий σ. Вычислить:

а) поток векторного поля F через полную поверхность пирамиды в направлении внешней нормали к её поверхности непосредственно;

б) тот же поток с использованием формулы Остроградского;

в) циркуляцию векторного поля F по замкнутому контуру λ непосредственно;

г) ту же циркуляцию – с использованием формулы Стокса.

F = (2z-3x-4y) j , p = 4z-3x-4y-4 = 0.

Решение.
	z
ABC	C 1
	A
n	-	4
	nAOC	3
B	nBOC 0	y
nAOB

x

Рисунок 14.6.

2а) Поток векторного поля F через полную поверхность пирамиды V (рис. 14.6), имеющей 4 грани равен сумме потоков через эти грани:

П F ndS .

ABC AOC AOB BOC

Для				ABC dS поверхность	АВС
	F		n
ABC
однозначно	проектируется на				все

координатные плоскости, поэтому можно выбрать любую из трёх формул (14.11).

Пусть	dS		dxdy			Тогда
			cos		.

ABC dS =

ABC

dxdy

F

n

F

n

cos

ABC

AOB

p

3i 4

4

grad

j

k

n ABC

Выбираем знак «+».Тогда

grad p

32 42

42

cosγ =

4

0

в формуле и cosγ>0 на рис.14.6, т.к. γ

41

4

3

4

= nABC Oz – острый . Окончательно: nABC

i

j

k

41

41

41

.

221