
- •Математическая экономика
- •230700 «Прикладная информатика»
- •Содержание
- •Предисловие
- •1.Модельповедения потребителя
- •Предпочтения потребителей
- •1.2. Функция полезности
- •1.3. Поверхности и кривые безразличия
- •1.4. Предельный анализ и эластичность
- •Перекрестная эластичность спроса по цене
- •Эластичность спроса по доходу
- •Предельная норма замещения
- •1.5. Модель поведения потребителя
- •1.6. Геометрическая интерпретация задачи максимизации полезности
- •1.7. Аналитическое решение задачи максимизации полезности
- •I способ. Приведение функции к одной переменной
- •II способ. Использование функции Лагранжа
- •1.8. Эффект компенсации. Уравнение Слуцкого
- •2. Модель поведения производителей
- •2.1. Производственная функция
- •2.2. Реакция производителей на изменение условий
- •2.3. Функции издержек
- •Задача на минимизацию издержек
- •2.4. Модели установления равновесной цены Дискретная паутинообразная модель рынка с запаздыванием предложения
- •Модель спроса и предложения Гудвина
- •Паутинообразная модель
- •Модель Эванса
- •3. Модели поведения фирмы на конкурентных рынках
- •3.1. Построение модели
- •3.2. Несовершенная конкуренция
- •3.3. Совершенная конкуренция
- •3.4. Монополия
- •3.5. Задача на максимизацию прибыли
- •4. Модель Леонтьева многоотраслевой экономики
- •4.1. Балансовые соотношения
- •4.2. Линейная модель многоотраслевой экономики
- •4.3. Продуктивные модели Леонтьева
- •Вопросы для самоконтроля
- •Список литературы
- •Математическая экономика
- •230700 «Прикладная информатика»
- •650992, Г. Кемерово, пр. Кузнецкий, 39
1.6. Геометрическая интерпретация задачи максимизации полезности
Если
на каком-то потребительском наборе
(x1,
x2),
бюджетное ограничение
![]() будет выполняться в виде строго
равенства, то мы можем увеличить
потребление какого-либо из продуктов
и тем самым увеличить функцию полезности.
Следовательно, набор
будет выполняться в виде строго
равенства, то мы можем увеличить
потребление какого-либо из продуктов
и тем самым увеличить функцию полезности.
Следовательно, набор![]() ,
максимизирующий функцию полезности,
должен обращать бюджетное ограничение
в равенство, то есть
,
максимизирующий функцию полезности,
должен обращать бюджетное ограничение
в равенство, то есть![]() .
Графически это означает, что решение
.
Графически это означает, что решение![]() задачи потребительского выбора должно
лежать на бюджетной прямой (см. рис. 7),
которую удобнее всего провести через
точки пересечения с осями координат,
где весь доход тратится на один продукт
задачи потребительского выбора должно
лежать на бюджетной прямой (см. рис. 7),
которую удобнее всего провести через
точки пересечения с осями координат,
где весь доход тратится на один продукт![]() и
и![]() .
.
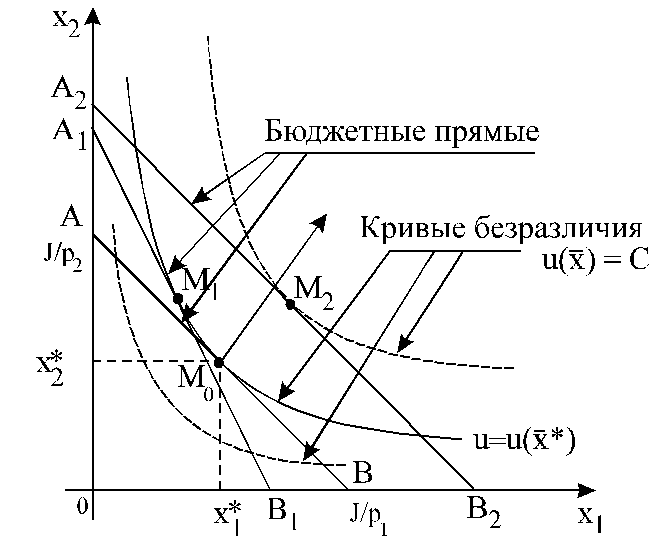
Рис. 8. Геометрическая интерпретация к определению
функции спроса исходя из модели поведения потребителя
Следовательно, при графическом решении задачи максимизации полезности, будем решать задачу вида:

![]()
Для построения графиков выполняем следующие шаги.
Строим бюджетную прямую
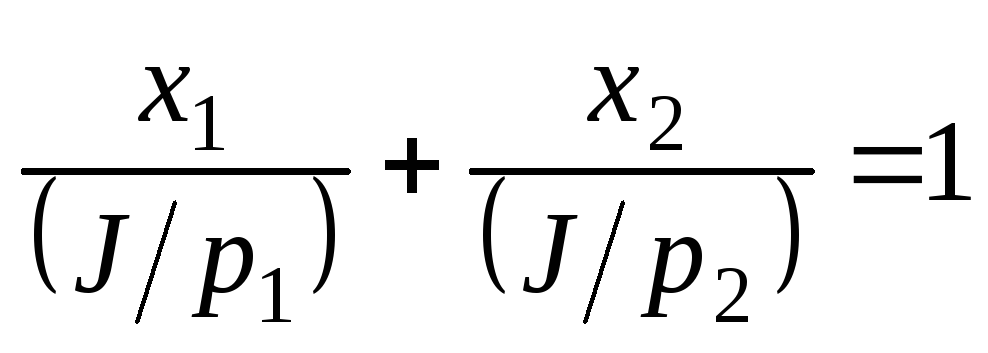 ,
на графике это прямаяAB,
которая проходит через точки
,
на графике это прямаяAB,
которая проходит через точки
 и
и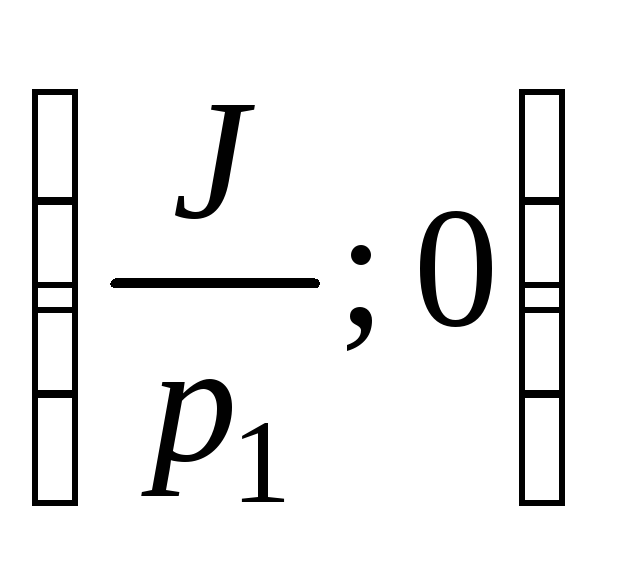 ;
;Строим кривые безразличия
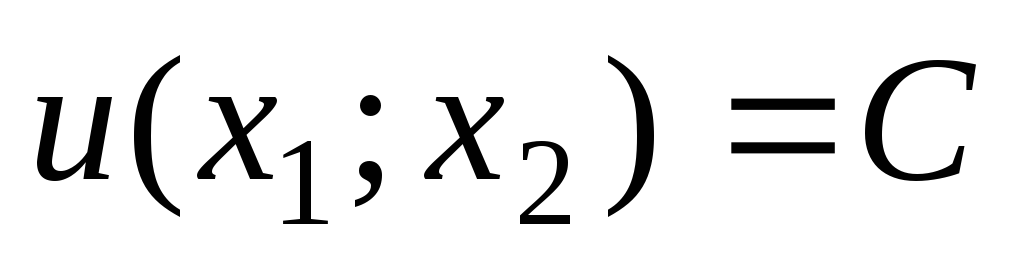 .
.Определяем точку
 на бюджетной прямойAB,
в которой кривая безразличия
на бюджетной прямойAB,
в которой кривая безразличия
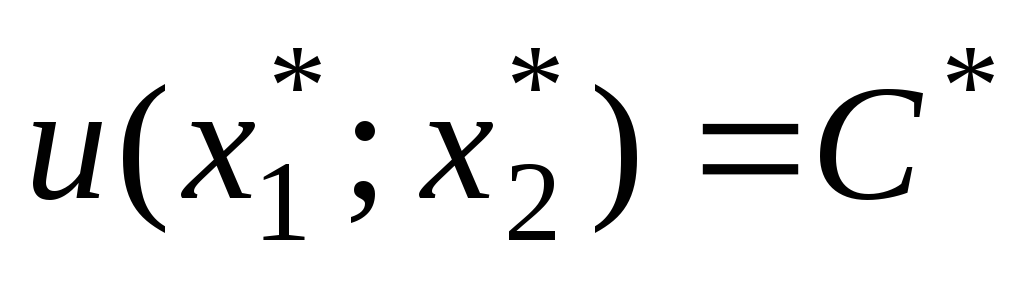 касается ее и получает в этой точке
максимально возможное значение C*.
касается ее и получает в этой точке
максимально возможное значение C*.
В
случае строгой вогнутости
![]() такая точка всегда единственна и
совпадает с точкой касания кривой
безразличия
такая точка всегда единственна и
совпадает с точкой касания кривой
безразличия![]() с бюджетной прямой
с бюджетной прямой![]() .
.
Выводы.
1. Треугольник AOB–ограничение множества выборов потребителя (бюджетное множество; бюджетное ограничение).
2.
Точка
![]() -
точка касания кривой безразличия и
бюджетной прямой есть оптимальное
решение задачи.
-
точка касания кривой безразличия и
бюджетной прямой есть оптимальное
решение задачи.
3. Линии AB и A1B1 соответствует одному и тому же размеру дохода, но разным ценам на товары x1 и x2.
4. Линия A2B2 (A2B2//AB) соответствует большему размеру дохода.
Пример
8. Найти
геометрическое решение задачи
максимизации индивидуальной функции
полезности
![]() при наличии бюджетных ограничений:
при наличии бюджетных ограничений:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
если
![]() ,
,![]() .
.
Решение.
1.
Из
![]() при p1
= 1, p2
= 3 и J
= 5 получаем:
при p1
= 1, p2
= 3 и J
= 5 получаем:
![]() –это
бюджетная прямая.
–это
бюджетная прямая.
Запишем
ее уравнение в отрезках
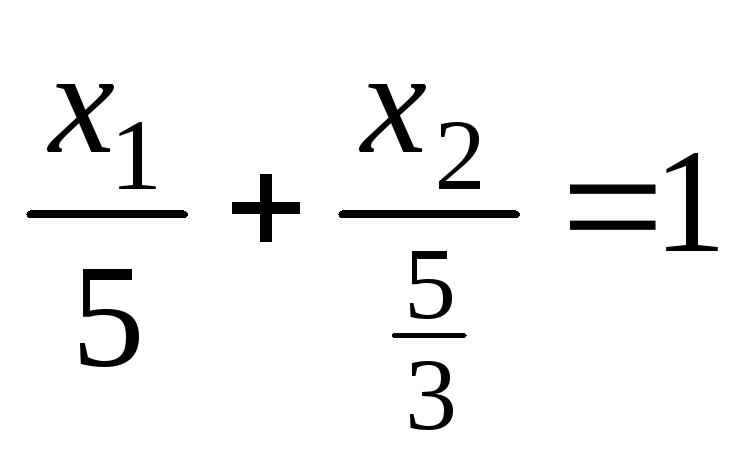 .
.
2. Построим на системе координат (см. на рис. 9)
а) бюджетную прямую АВ;
б)
кривую безразличия
![]() ,
то есть
,
то есть![]() .
.
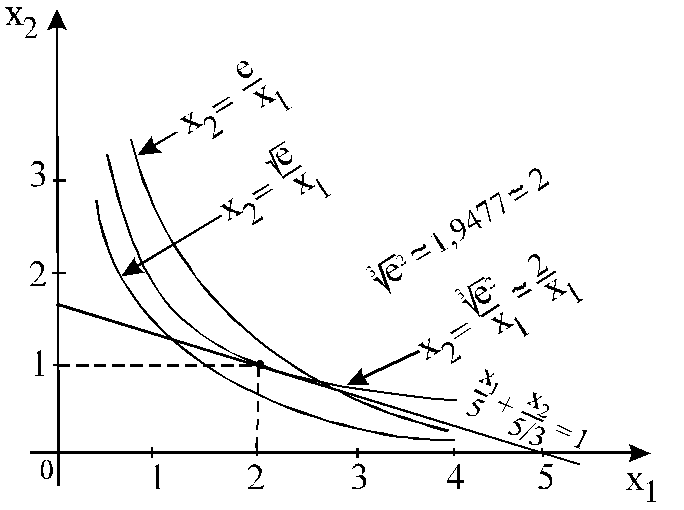
Рис. 9. Графическое решение примера 7
3. Решим систему уравнений графически
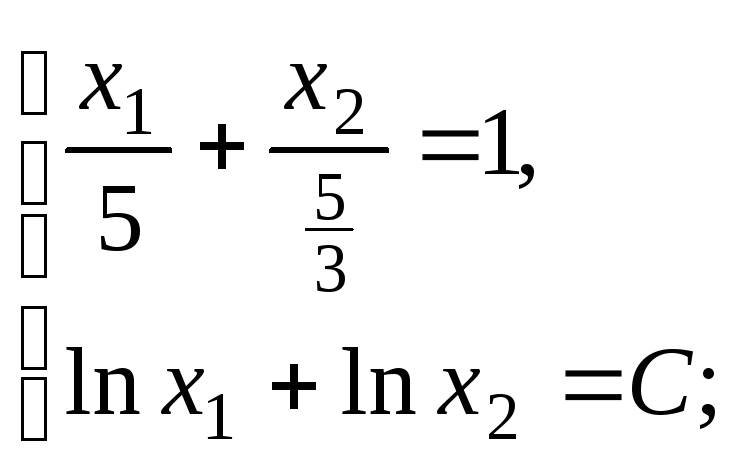
![]() ,
,
![]() ,
,![]() –гипербола.
–гипербола.
1)
![]() при С
= 1; 2)
при С
= 1; 2)
![]() при
при
![]() ;
;
3)
![]() при
при
![]() .
.
Ответ: x1 2; x2 1.
1.7. Аналитическое решение задачи максимизации полезности
Задачу потребительского выбора можно заменить задачей на условный экстремум
![]() (22)
(22)
при условии
![]()
Для решения этой задачи на условный экстремум применим метод Лагранжа.
Выписываем функцию Лагранжа
![]() ,
(23)
,
(23)
где - неопределенный множитель Лагранжа.
Экономический смысл этого множителя: если цены pi и доход J меняются в одно и то же число раз , то функция полезности, а значит, и решение задачи потребительского выбора не изменится.
Далее находим ее первые частные производные по переменным x1, x2 и , приравниваем эти частные производные к нулю:
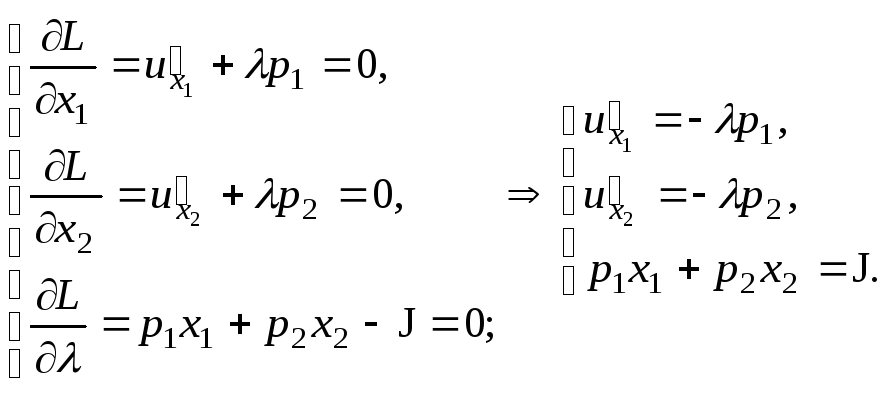
Исключив из полученной системы трех уравнений с тремя неизвестными неизвестную (разделив поэлементно первое уравнение на второе), получим систему двух уравнений с двумя неизвестнымиx1и x2:
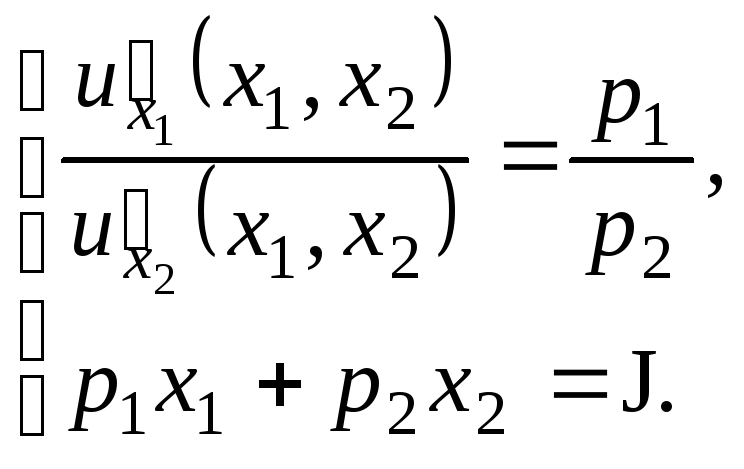
Решение
![]() этой системы есть критическая точка
функции Лагранжа. Подставим решение
этой системы есть критическая точка
функции Лагранжа. Подставим решение![]() в левую часть равенства
в левую часть равенства
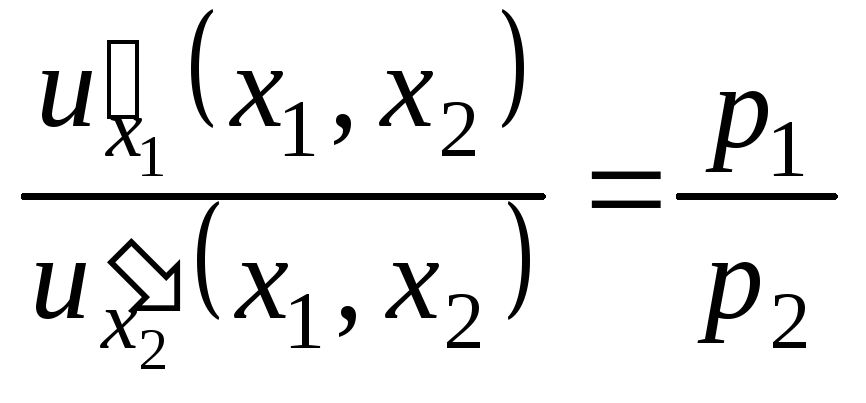 .
.
Получим,
что в точке
![]() локального рыночного равновесия
индивидуума отношение
локального рыночного равновесия
индивидуума отношение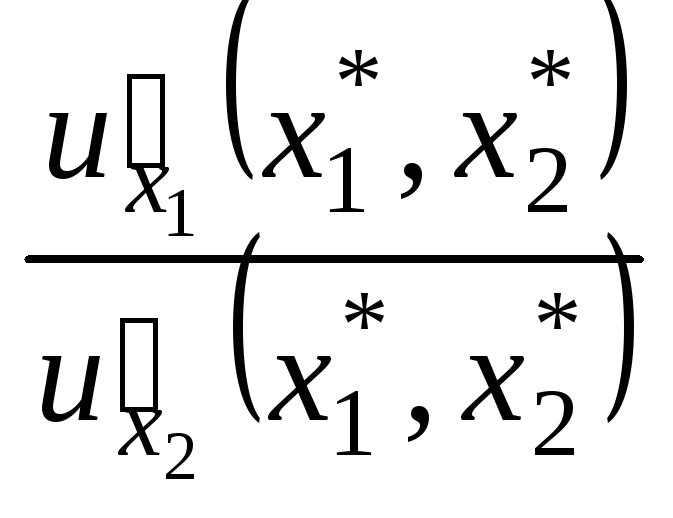 предельных полезностей
предельных полезностей![]() и
и![]() продуктов равно отношению рыночных
ценp1и
p2на эти
продукты:
продуктов равно отношению рыночных
ценp1и
p2на эти
продукты:
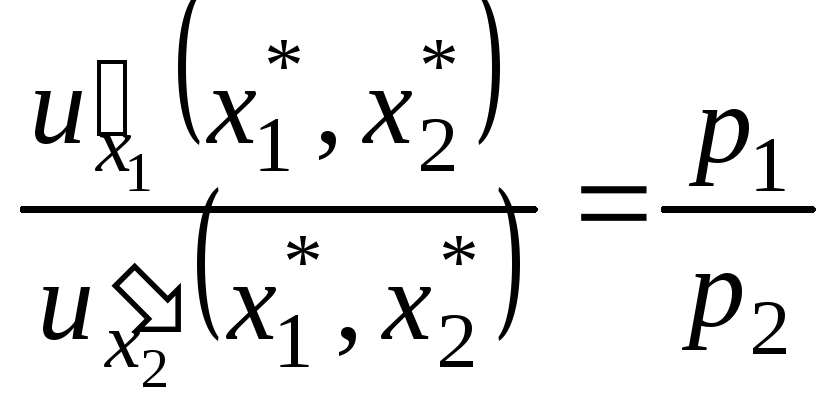 .
(24)
.
(24)
В
связи с тем, что отношение
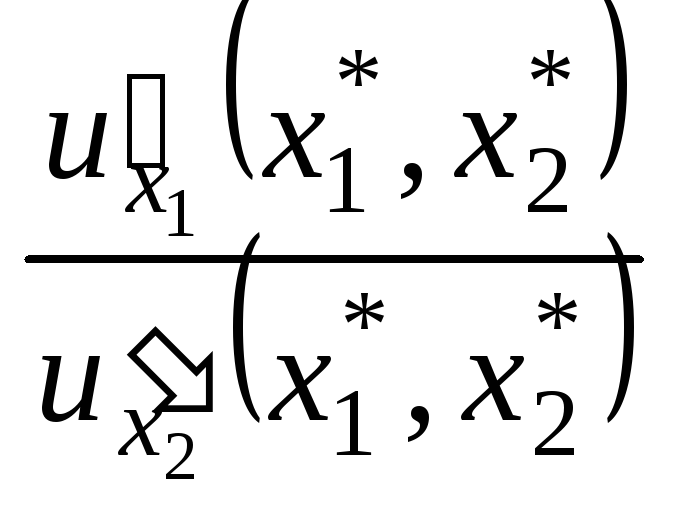 равно предельной норме замены первого
продукта вторым в точке локального
рыночного равновесия
равно предельной норме замены первого
продукта вторым в точке локального
рыночного равновесия![]() ,
из (24) следует, что эта предельная норма
равна отношению рыночных цен
,
из (24) следует, что эта предельная норма
равна отношению рыночных цен![]() на продукты. Приведенный результат
играет важную роль в экономической
теории.
на продукты. Приведенный результат
играет важную роль в экономической
теории.
А именно,
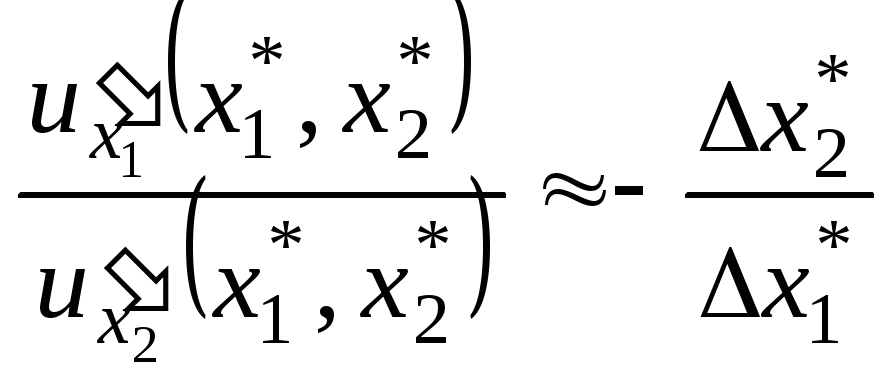 ;
;
![]() ,
(25)
,
(25)
то есть
отношение (со знаком минус) конечных
(относительно небольших) изменений
![]() к
к![]() объемов продуктов в локальном рыночном
равновесии
объемов продуктов в локальном рыночном
равновесии![]() приближенно равно отношению рыночных
ценp1 и
p2на
продукты.
приближенно равно отношению рыночных
ценp1 и
p2на
продукты.
Равенство (25) позволяет давать приближенные оценки отношению рыночных цен, если известны конечные изменения объемов продуктов относительно потребительского набора, приобретенного потребителем, то есть набора, который естественно следует толковать в качестве оптимального для потребителя.
Пример
9.Найти аналитическое решение задачи
максимизации индивидуальной функции
полезности![]() при наличии бюджетного ограничения
при наличии бюджетного ограничения
![]() ,
если
,
если
![]() иJ=5.
иJ=5.
Решение.
Известны:

Требуется
найти значения
![]() .
.
