Неустановившееся истечение газа из сосуда конечного объема через малое отверстие. Предположим, что площадь

	n
n	na

va = va na

n

Рис. 2.3. Опорожнение сосуда с газом

проходного сечения отверстия мала по сравнению с поперечным сечением сосуда (рис. 2.3). В этом случае можно пренеб-

речь движением	газа	внутри
сосуда (v ≈ 0 )	и	принять,

что параметры газа в сосуде

зависят только от	времени:
ρ(x ,y,z ,t) ≈ ρ0 (t) .	Здесь ин-

декс 0 соответствует неподвижному газу в сосуде (или, как принято говорить, состоянию торможения). Предположим, что в сечении выходного отверстия а −а , площадь которого равна F , параметры течения распределены равномерно. В частности, плотность и скорость газа равны ρa и va (см. рис. 2.3). Тогда исходя из (2.1) получим

V	dρo	+ρ v F = 0 ,	V	dρ0	= −Q ,	(2.10)
	dt	a a a		dt

где Q = ρava Fa – расход газа в выходном отверстии. Уравнение (2.10) выражает закон сохранения массы при опорожнении сосуда.

2.2. Уравнение количества движения

Уравнение количества движения представляет собой математическую запись закона об изменении количества движения (второго закона Ньютона). Согласно этому закону, скорость измене-

ния количества движения K жидкости в движущемся объеме V , состоящем из одних и тех же частиц, равна главному вектору всех внешних сил, действующих на рассматриваемую массу жидкости, т.е.

dK	= R .	(2.11)
dt

Количество движения жидкости в объеме V в момент времени t , по определению, равно: K = ∫∫∫ρvdV . Главный вектор

V

139

всех внешних сил R , действующих на жидкость в объеме V в любой момент времени t , складывается из суммы объемных и поверхностных сил.

Объемные силы – это силы, аддитивные по объему жидкости (или, что то же, по массе, так как масса аддитивна по объему). Они действуют на любую частицу жидкости, находящуюся внутри объема. Суммарная объемная сила, действующая на жидкость в объе-

ме V , может быть представлена в виде ∫∫∫ρFdV , где F – сила,

V

действующая на единицу массы жидкости. Последнюю называют также плотностью массовых сил. Сила ρF действует на единицу

объема жидкости, и ее называют плотностью объемных сил . Поверхностные силы – это силы, действующие на жидкость в

объеме V со стороны жидкости вне V по поверхности S , ограничивающей объем. Суммарная поверхностная сила, действующая на единичную площадку поверхности S , называется напряжением. Напряжение на элементарной площадке dS , ориентация которой в пространстве задана вектором единичной внешней нормали n , обозначим πn . В механике жидкости и газа напря-

жение πn можно представить в виде суммы двух составляющих: связанной с давлением p и равной −pn , и составляющей τn ,

обусловленной вязкостью. Вторая составляющая включает в себя, в частности, напряжение трения, которое направлено по касательной к dS . Величина давления p не зависит от ориентации

площадки в данной точке. Давление действует по нормали к dS в направлении, противоположном вектору n . Суммарная сила

давления, действующая на поверхность S ,		равна: − ∫∫pndS , а
		S
суммарная сила,	обусловленная вязкостью,	∫∫τn dS . Как полное
		S
напряжение πn ,	так и вязкое напряжение	τn зависят в данной

точке потока от ориентации нормали n , что подчеркивается индексом n . В отличие от плотности массовых сил F (отметим,

что вектор F зависит в общем случае только от координат рассматриваемой точки в потоке и времени), напряжения в жидкости

140

векторного поля не образуют, так как зависят как от положения рассматриваемой точки, так и от ориентации в ней вектора n . Напряжения описываются более сложным математическим объектом, а именно тензором второго ранга.

Возвращаясь к закону изменения количества движения и подставляя в правую часть (2.11) сумму объемных и поверхностных сил, получим

	dK	= ∫∫∫ρFdV − ∫∫ pndS + ∫∫τn dS .			(2.12)
	dt
		V	S	S

Используем формулу (1.34) для вычисления производной по времени в левой части (2.12):

ddtK = ∫∫∫V ∂∂ρtv dV + ∫∫S ρvvn dS .

Подставляя это соотношение в (2.12), получим уравнение закона изменения количества движения в интегральной форме в окончательном виде:

∫∫∫				→
	∂ρv dV + ∫∫ρvvndS = ∫∫∫ρF dV − ∫∫pndS + ∫∫τn dS , (2.13)
V	∂t	S	V	S	S

которое представляет собой математическую формулировку второго закона Ньютона в механике жидкости и газа.

Используя формулы (1.35) и (1.42), перейдем от интегральной формы записи этого закона к дифференциальной:

∂ρv

+

ρvvx

+

∂ρvvy

+

∂ρvvz

= ρF − p +

∂ τx

+

∂ τy

+

∂ τz

.

∂t

∂x

∂y

∂z

∂x

∂y

∂z

Расписывая подробно производные от произведений в левой части и учитывая уравнение неразрывности (2.3) и выражение для полной производной по времени (1.17), получим уравнение количества движения в дифференциальной форме в окончательном виде:

ρ

dv

= ρF

− p +

∂ τ

x

+

∂ τy

+

∂ τ

z

,

(2.14)

dt

∂y

∂z

∂x

где p =

∂p →

+

∂p →

+

∂p →

∂x

i

∂y

j

∂z

k – градиент давления.

141

Векторы τx ,τy ,τz описывают напряжения на площадках с

нормалями i , j и k . Запишем выражения для этих векторов через их проекции на оси координат x ,y,z :

→	→	→	→
τx	= τxx i	+ τxy j	+ τxz k
→	→	→	→
τy = τyx i		+ τyy j	+ τyz k
→	→	→	→
τz	= τzx i	+ τzy j	+ τzz k

Девять величин τxx ,τxy и т.д. в совокупности представляют

собой компоненты тензора вязких напряжений. Рассматривая закон изменения момента количества движения для среды без внутренних моментов, каковой является вода, воздух и вообще большинство обычных жидкостей и газов, можно строго доказать, что τxy = τyx ; τxz = τzx ; τyz = τzy . Эти равенства означают,

что тензор вязких напряжений симметричен.

Во многих случаях поле плотности массовых сил потенци-

ально, т.е. вектор F можно представить в виде градиента неко-

→

торой скалярной функции F = − Φ . Функция Φ называется потенциалом массовых сил (знак «минус» перед Φ введен для удобства дальнейших выкладок и не влияет на свойство потенци-

альности). В случае сил тяжести Φ = gz							( z – вертикальная ко-
ордината			–	направлена вверх		от поверхности Земли)		и
→	= −	∂Φ →		→
F		∂z	k = −g k .
	Если			вязкие	напряжения	не	учитываются,	т.е.

τx = τy = τz = 0 , то жидкость называется идеальной или невяз-

кой. В этом случае уравнение количества движения принимает, вместо (2.14), существенно более простой вид:

ρdv	→	− p .	(2.15)
	= ρF
dt

Это уравнение впервые было получено Леонардом Эйлером и называется его именем. В проекции на оси x , y и z оно за-

пишется так:

142

ρ

dvx

= ρF

x

−

∂p ,

ρ

dvy

= ρF

−

∂p

,

ρdvz

= ρF

− ∂p .

∂y

dt

∂x

dt

y

dt

z

∂z

Если течение установившееся и одномерное и массовые силы

не учитываются, т.е. принимается

∂

=

∂

=

∂

=vy =vz = 0 и

∂t

∂y

∂z

Fx = 0 , то из уравнения Эйлера в проекции на ось x ,

опуская

индекс у vx , можно получить следующую очень простую форму записи уравнения количества движения:

						ρvdv = −dp .				(2.16)
		Иногда выражение					для полной производной	dv		в (2.15)
								dt
	удобно			использовать в			форме Громеки – Лэмба	(см.		(1.18))
	dv	=	∂v	+	v 2	+ Ω×v ,	где Ω = ×v ≡ rot v . В этом случае
	dt		∂t		2

уравнение количества движения при потенциальности массовых сил запишется в виде

∂v			v 2			p
	+ Ω×v = −	Φ +			−		.	(2.17)
∂t			2			ρ

Рассмотрим некоторые примеры записи уравнения количества движения в конкретных ситуациях. Будем исходить из интегральной формы (2.13).

Течение газа через скачок уплотнения. Рассмотрим устано-

вившееся течение газа через поверхность разрыва (см. рис. 2.2). Будем считать газ идеальным и пренебрежем объемными силами. Если записать в этом случае уравнение (2.13) для элементарного цилиндра с основаниями 1–1 и 2–2, содержащего внутри себя поверхность разрыва, а затем перейти к пределу при стремлении к нулю высоты цилиндра, то получим следующее соотношение, которое представляет собой уравнение количества движения на скачке уплотнения и связывает параметры до и после скачка:

ρ2 (+v2n )v2	+ ρ1 (−v1n )v1 = −(p2 − p1 )n .	(2.18)
правая грань 2−2	левая грань 1−1

Это векторное соотношение, записанное в проекциях на на-

→

правления нормали к скачку n и касательной τ, примет вид

143

ρ v 2	− ρ v 2		= p − p	2	,	(2.19)
2 2n	1 1n		1
	v2τ	=v1τ .				(2.20)

Из второго равенства, кстати, следует, что касательная составляющая скорости при перетекании газа через скачок уплотнения не терпит разрыва.

Уравнение количества движения для газового эжектора.

Запишем уравнение количества движения для течения в газовом эжекторе с цилиндрической камерой смешения (рис. 2.4). Обозначим площади сечений 1–1, 2–2 и 3–3 соответственно F1 , F2 и

F3 . Будем считать параметры газа в этих сечениях равными не-

которым средним значениям. Пренебрегая объемными силами и трением газа о стенки, получим из уравнения (2.13) соотношение

ρ1v1( −v1 )F1 + ρ2v2 ( −v2 )F2 + ρ3v32F3 = p1F1 + p2F2 − p3F3 , (2.21)

которое и выражает закон изменения количества движения в рассматриваемом течении.

2			3
ρ2 v2	p2		ρ3
2
1	ρ1 v1	p1	v3
			p3
2			3

Рис. 2.4. Газовый эжектор

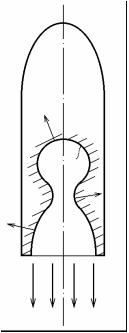
Величина реактивной силы ракетного двигателя. Вос-

пользуемся теперь уравнением (2.13) для получения величины реактивной силы ракетного двигателя (рис. 2.5). Считая течение установившимся, запишем (2.13) для массы газа, заключенной в произвольный момент t в объеме камеры и сопловой части, который ограничен стенками w и выходным сечением a −a сопла:

∫∫ρvvndS + ∫∫ ρvvndS =

	w	a−a
= −∫∫pn dS + ∫∫τndS − ∫∫			pn dS + ∫∫ τndS .	(2.22)
w	w	a−a	a−a
		144

		Слагаемое	∫∫ρvvndS характери-
			w
		зует подвод	продуктов	сгорания
		внутрь этого объема. Оно может опи-
		сывать впрыск топлива и окислителя в
n		камеру сгорания в случае жидкостного
		ракетного двигателя или же приток
		продуктов сгорания с поверхности то-
w		плива в случае ракетного двигателя на
	n	твердом топливе. Однако в обоих слу-
		чаях это слагаемое является,		как пра-

nвило, несущественным из-за малого значения нормальной составляющей скорости vn подводимой массы. По-

a	a	этому примем		∫∫ρvvndS = 0 .
				w
	na	Силы вязкости в выходном сече-
		нии сопла, описываемые слагаемым
Рис. 2.5. К определению		∫∫ τndS ,	пренебрежимо		малы по
величины реактивной силы		a−a
		сравнению	с	силами	давления

∫∫ pn dS , поэтому положим ∫∫ τndS = 0 .

a−a

a−a

Учитывая сделанные упрощающие допущения, перепишем уравнение количества движения (2.22):

∫∫ ρvvndS = −∫∫pn dS + ∫∫τndS − ∫∫ pn dS .				(2.23)
a−a	w	w	a−a

Здесь два первых слагаемых в правой части представляют собой суммарную силу (сумму сил давления и вязких сил трения), действующую на газ со стороны стенок камеры и сопловой части. Согласно третьему закону Ньютона сила, действующая со

стороны газа на стенки двигателя (обозначим ее Pп ), равна по величине указанной выше силе, но противоположна ей по знаку. Сила Pп и есть реактивная сила двигателя, обусловленная воздействием истекающих газов на его стенки. Поскольку в силе Pп

145

не учитывается воздействие окружающей среды, то она представляет собой реактивную силу в пустоте и ее называют пустотной тягой двигателя. В силу сказанного выше пустотная тяга равна:

Pп = +∫∫pn dS − ∫∫τndS .		(2.24)
w	w

Это соотношение можно переписать с учетом (2.23) в виде

Pп = − ∫∫ ρvvndS − ∫∫ pn dS .		(2.25)
a−a	a−a

Чтобы учесть влияние окружающей среды на величину реактивной силы, введем в рассмотрение наружное давление pн , т.е.

давление в среде, в которую истекает струя ракетного двигателя. Это давление приложено к каждому элементу поверхности двигателя в направлении, противоположном направлению внешней нормали n . Таким образом, чтобы учесть воздействие наружного

давления на двигатель, нужно к значению пустотной тяги Pп добавить слагаемое −∫∫pнn dS . В результате реактивная сила с

w

учетом окружающей среды будет равна:

P = Pп − ∫∫pнn dS = ∫∫( p − pн )n dS − ∫∫τndS .			(2.26)
w	w	w
Используя далее очевидное соотношение
∫∫pнn dS = −∫∫pнn dS − ∫∫ pнn dS = 0 ,
S	w	a−a

получим формулу для определения величины реактивной силы:

P = − ∫∫ ρvvndS − ∫∫ ( p − pн )n dS .		(2.27)
a−a	a−a

Если двигатель является односопловым и параметры газового потока на срезе сопла можно считать постоянными по сечению, то выражение для реактивной силы принимает очень простой вид, который часто используется в расчетах:

P = −Qva −(pa − pн )na Fa ,	(2.28)
где Fa – площадь выходного сечения сопла,	Q = ρava Fa . Знак

«минус» в первом слагаемом свидетельствует о том, что реактив-

146