ШАГ 3. ПЛОСКОСТЬ. ТОЧКА И ЛИНИИ В ПЛОСКОСТИ
3.1.Задание плоскости на чертеже. Точка в плоскости
Воснованиях планиметрии (геометрии на плоскости) плоскость – это то пространство, та среда, где выполняются аксиомы и «разыгрывается» основанная на них геометрия.
Положение плоскости в пространстве однозначно определяется тремя точками, не лежащими
на одной прямой (рис. 3.1). Это самый общий способ задания плоскости α( A, B,C) .
Если через две точки (скажем, B и C ) провести прямую l , то она будет лежать в этой плоскости, а плоскость будет задана прямой l и точкой A (т.е. α(l, A) ), что иллюстрируется рис. 3.2.
Проведем еще одну прямую m , проходящую через точки A и C (рис. 3.3). Плоскость будет задана двумя пересекающимися прямыми l и m ( α(l, m) ).
Плоскость может быть задана и двумя параллельными прямыми. Такое задание плоскости мы получим, если через точку A проведем прямую n , параллельную прямой l ( α(l, n) рис. 3.4).
Соединив точки A, B, C отрезками прямых линий (рис. 3.5), получим плоскость α , заданную треугольником ABC, что записывается как α( ABC) .
Остановимся на очень важном свойстве плоскости, часто использующемся при решении задач и называемом свойством принадлежности, – точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.
Если рассмотреть плоскость, заданную прямой l и точкой A, то какую бы точку мы ни взяли на прямой l, она будет принадлежать данной плоскости. На рис. 3.6 точки K, L, M принадлежат прямой l, а следовательно, все они лежат в плоскости α( A,l) . (Напоминаем, что точка принад-
лежит прямой, если ее проекции лежат на одноименных проекциях прямой. )
Решим простейшую задачу. Плоскость задана пересекающимися прямыми a и b; задана фронтальная проекция точки C, лежащей в этой плоскости. Необходимо построить горизонтальную проекцию этой точки. Исходные данные задачи приведены на рис. 3.7,а.
В данном случае фронтальная проекция точки C лежит на фронтальной проекции прямой b. Точка C будет принадлежать плоскости, если будет лежать на прямой b, принадлежащей этой плоскости. Чтобы это условие выполнилось, необходимо, чтобы горизонтальная проекция точки C лежала на горизонтальной проекции прямой b. Опустив линию проекционной связи и обозначив полученную проекцию точки, мы завершим решение данной задачи (рис. 3.7,б).
Усложним рассмотренную задачу – построим недостающую проекцию точки, принадлежащей плоскости. Исходные данные приведены на рис. 3.8,а. Здесь точка D не лежит ни на одной из прямых, задающих плоскость β(a,b) . Следовательно, нам надо построить вспомогательную прямую,
лежащую в плоскости β и проходящую через точку D.
Такое построение приведено на рис. 3.8,б. Здесь мы через фронтальную проекцию точки D провели фронтальную проекцию вспомогательной прямой m так, чтобы эта прямая пересекала прямые a и b. Отметим точки пересечения прямой m с прямыми a и b. Это точки 1 и 2. Их фронтальные проекции лежат на фронтальных проекциях пересекающихся прямых, задающих плоскость (рис. 3.8,в).
Поскольку точка 1 лежит на прямой a, а точка 2 – на прямой b, легко можно построить горизонтальные проекции указанных точек, а соединив их, получить горизонтальную проекцию пря-
мой m (рис. 3.8,г).
Теперь для решения задачи необходимо сделать последний шаг: зная фронтальную проекцию точки D, принадлежащей вспомогательной прямой m, построить горизонтальную проекцию этой точки. Это легко сделать с помощью линии проекционной связи (рис. 3.8,д). Решение готово.
3.2. Следы плоскости
След плоскости – это прямая линия, по которой плоскость пересекается с плоскостью проекций. Поскольку плоскостей проекций у нас три, то соответственно и следов тоже три: горизонтальный ( h0α ), фронтальный ( f0α ) и профильный ( p0α ). Это иллюстрируется рис. 3.9.
Очевидно, что след плоскости – это прямая частного положения, так как она принадлежит одновременно как рассматриваемой плоскости, так и одной из плоскостей проекций. Из последнего следует, что у всех точек следа одна из координат равна нулю.
29
p2 |
C" |
|
|
|
A" |
C" |
|
|
|
|
|||
A" |
B" |
C |
a(A,B,C) |
|
|
B" |
|
|
|
||||
|
A |
B |
|
|
x |
|
|
|
|
|
|
|
|
|
A' |
C' |
|
|
A' |
C' |
|
|
|
|
|||
|
B' |
|
p1 |
|
|
B' |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Рис. 3.1 |
|
|
l" |
A" |
l" |
C" |
|
A" |
|
|
|
|
|
||||
x |
B" |
|
|
x |
|
|
|
|
|
|
|
||
A' |
l' |
C' |
|
A' |
|
l' |
|
|
|
||||
|
B' |
|
Рис. 3.2 |
|
|
|
|
|
|
|
|
|
|
A" |
m" |
C" |
|
|
|
m" |
|
|
|
|
|
||
|
l" |
|
|
|
l" |
|
|
|
|
|
|
||
x |
B" |
|
|
x |
|
|
|
|
|
|
|
||
A' |
m' |
C' |
|
|
|
m' |
|
|
|
|
|
||
|
l' |
|
|
|
l' |
|
|
B' |
|
Рис. 3.3 |
|
|
|
|
|
|
|
|
||
|
n" |
l" |
|
|
|
|
|
|
|
n" |
|
|
|
A" |
|
C" |
|
|
|
|
|
|
|
|
|
||
|
B" |
|
|
|
|
l" |
x |
|
|
x |
|
|
|
|
|
|
|
|
||
|
n' |
l' |
|
|
|
|
|
|
|
n' |
|
|
|
A' |
|
C' |
|
|
l' |
|
|
B' |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.4 30
A" 
C"
B"
x
C'
A'
B'
Рис. 3.5
a"
C"
b"
b'
a'
à
Рис. 3.7
31
M" l"
A" L" K"
x
l'
A' M' L'
K'
Рис. 3.6
a"
C"
b"
b'
C'
a'
á
a"
D"
b"
b'
a'
a
a"
m"
1"
D"
2"
b"
b'
a'
â
a"
m"
1"
D" |
|
|
2" |
|
b" |
|
b' |
|
2' |
D' |
a' |
m' 1' |
|
ä |
|
Рис. 3.8 |
|
m"
D"
á
m"
1"
D"
m' 1'
ã
a"
b"
b'
a'
a"
2"
b"
b'
2'
a'
32
Z
foa p3
poa
p2
x
hoa |
y |
|
p1 |
Рис. 3.9
Рассмотрим в качестве примера фронтальный след плоскости. Он принадлежит фронтальной плоскости проекций, следовательно, у всех его точек координата y равна нулю, поэтому фронтальная проекция следа совпадает с самим следом (т.е. f0α ≡ f0′′α ), а горизонтальная – с осью X
(рис. 3.10). Если на фронтальном следе взять какую-либо точку, то ее проекции, естественно, будут расположены на соответствующих проекциях следа (например, точка 1).
Дополним рис. 3.10 изображением горизонтального следа h0α (рис. 3.11). Горизонтальная проекция этого следа совпадает с самим следом ( h0α ≡h0′α ), а фронтальная – с осью X (это потому, что у
всех точек следа координата z=0). Показанная на рисунке точка 2 принадлежит горизонтальному следу. Оба следа пересекаются в одной точке на оси X. Эта точка называется точкой схода следов.
f0a f0a
1 1
x |
1' |
f0a |
|
Рис. 3.10 |
|
f0a f0a
1 1"
x |
1' |
2" |
f0a h0a |
точка схода следов
2 2' |
h0a h0a |
Рис. 3.11 |
|
33
Прежде чем рассмотреть несколько примеров на построение точек, принадлежащих следам, отметим следующее.
1.Если точка принадлежит горизонтальному или фронтальному следу, то одна ее проекция лежит на соответствующем следе (совпадает с самой точкой), а вторая проекция – на оси X.
2.Следы плоскости, как и любая прямая в плоскости, предполагаются бесконечными.
На рис. 3.12 проиллюстрированы проекции точек, принадлежащих следам плоскости. Плоскость β, следы которой изображены на рис. 3.12,в, называется плоскостью со сливающимися следами.
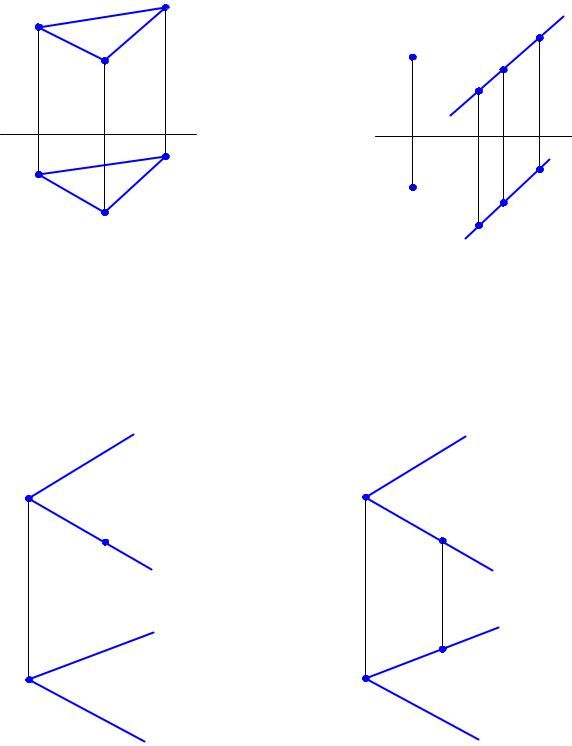
Задание плоскости следами (а это частный случай задания плоскости пересекающимися прямыми) является самым наглядным для представления положения плоскости в пространстве. В самом деле, возьмите чертеж с изображением следов плоскости (рис. 3.13,а) и согните его под прямым углом так, чтобы линия сгиба проходила по оси X, как на рис. 3.13,б. Положение плоскости в пространстве стало достаточно наглядным.
Мы рассмотрели построение проекций точек, принадлежащих следам плоскости. Теперь возьмем какую-либо точку, не лежащую на следе. Пусть задана фронтальная проекция точки A, принадлежащей плоскости α(h0α, f0α) (рис. 3.14,а). Вспомним, что точка принадлежит плоскости,
если она принадлежит прямой, лежащей в этой плоскости. Поэтому для решения задачи через точку A необходимо провести вспомогательную прямую l, лежащую в плоскости α . Проведем фронтальную проекцию этой прямой (рис. 3.14,б). Прямую l надо провести так, чтобы она пересекала оба следа плоскости (тогда легче построить вторую проекцию этой прямой), поэтому фронтальная проекция должна пересечь фронтальный след и ось X. Тогда и получатся две точки на следах: точка 1 на фронтальном следе и точка 2 – на горизонтальном. Построим горизонтальные проекции точек 1 и 2 (рис. 3.14,г) и соединим их. Получим горизонтальную проекцию вспомогательной прямой l. Положение горизонтальной проекции точки A определится с помощью линии проекционной связи (рис. 3.14,д). Задача решена.
Обратите внимание на рис. 3.14,е. Здесь построены проекции точек B и C. Обе эти точки лежат на прямой l. Таким образом, все указанные точки (и 1, и 2, и A и вновь построенные B и C) принадлежат плоскости α .
На рис. 3.15 приведено решение аналогичной задачи. Здесь через точку A проведена вспомогательная прямая 1 - 2, причем точка 1 лежит на фронтальном, а 2 – на горизонтальном следе. Естественно, что решение будет выглядеть абсолютно одинаково, если при заданной фронтальной
проекции точки A построить горизонтальную, или наоборот. |
|
|||
|
|
f0a |
|
f0a |
|
|
A" |
|
|
x |
B" |
A' |
x |
C" |
h0a |
B' |
|
h0a |
C' |
|
|
|
|
|
|
|
à |
|
á |
D" f0b
F'
x |
E" |
G' |
|
|
F" D'
G"
E'
h0b
âРис. 3.12
34
|
|
f0a |
|
|
f0a |
|
|
|
|
|
|
|
|
a |
|
||
|
|
|
|
|
|
|
||
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
h0a |
|
|
|
|
h0a |
|
|
|
|
|
|
|
a |
|
Рис. 3.13 |
á |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
f0a |
|
|
l" |
f0a |
||
|
|
A" |
|
|
|
A" |
|
|
x |
|
|
x |
|
|
|
|
|
|
|
h0a |
|
|
á |
|
h0a |
|
|
à |
|
|
|
|
|
||
|
l" |
f0a |
|
|
l" |
|
f0a |
|
|
1" |
|
|
|
1" |
|
|
|
|
|
A" |
|
|
|
A" |
|
|
x |
|
2" |
x |
|
1' |
|
2" |
|
|
|
h0a |
|
|
|
|
2' |
|
|
|
|
|
|
|
h0a |
||
|
â |
|
|
|
ã |
|
||
|
|
|
|
|
|
|||
|
l" |
f0a |
|
l" |
|
|
|
|
|
|
B" |
|
f0a |
|
|||
|
1" |
|
|
|
|
|||
|
|
|
|
1" |
|
|||
|
|
A" |
|
|
|
|
||
|
|
|
|
A" |
|
|||
x |
1' |
2" |
|
B' |
|
|||
x |
1' |
2" |
||||||
|
|
A" |
|
|||||
|
|
2' |
|
|
A" |
C" |
||
|
ä |
h0a |
|
|
|
2' |
||
|
|
f0a |
e |
|
C' |
h0a |
||
|
A" |
|
|
l' |
||||
|
|
Рис. 3.14 |
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
35 |
|
|
|
|
|