22. ПЕРЕМЕННЫЕ И ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ОПЕРАЦИИ В MATHCAD
22.11. Стандартные математические функции
Основная нагрузка, если можно так выразиться, в процессе решения практически любой задачи ложится на ядро из стандартных математических функций, которые приведены и кратко описаны в табл. 22.2.
Таблица 22.2
|
Функция |
Описание |
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
acos(z) |
Арккосинус от z |
|
|
|
acosh(z) |
Гиперболический арккосинус от z |
|
|
|
acot(z) |
Арккотангенс от z |
|
|
|
acoth(z) |
Гиперболический арккотангенс от z |
|
|
acsc(z) |
Арккосеканс от z |
|
|
|
acsch(z) |
Гиперболический арккосеканс от z |
|
|
|
asec(z) |
Арксеканс от z |
|
|
|
asech(z) |
Гиперболический арксеканс от z |
|
|
|
asin(z) |
Арксинус от z |
|
|
|
asinh(z) |
Гиперболический арксинус от z |
|
|
|
atan(z) |
Арктангенс от z |
|
|
|
|
|
Функцией в качестве результата возвращается угол (в радианах) между |
|
|
atan2(x,y) |
осью Ох и прямой, проходящей через начало координат иточку с коор- |
|
||
|
|
динатами х и у. Другими словами, atan2(x,y) = atan(y/x) |
|
|
atanh(z) |
Гиперболический арктангенс от z |
|
|
|
cos(z) |
Косинус от z |
|
|
|
cosh(z) |
Гиперболический косинус от z |
|
|
|
cot(z) |
Котангенс от z |
|
|
|
|
coth(z) |
Гиперболический котангенс от z |
|
|
|
esc(z) |
Косеканс от z |
|
|
|
csch(z) |
Гиперболический косеканс от z |
|
|
|
exp(z) |
Показательная функция (е ≈ 2.72 в степени z) |
|
|
|
Г(z) |
Гамма-функция Эйлера от z. Вычисляется как Г(z) = ∞∫t z−1 exp(−t)dt |
|
|
|
|
0 |
|
|
|
ln(z) |
Логарифм натуральный от z |
|
|
|
lnГ(z) |
Логарифм натуральный от гамма-функции Эйлера с аргументом z. |
|
|
|
|
Символ Г можно ввести так: сначала ввести большую литеру G (ком- |
|
|
|
|
бинация клавиш <Shift>+<G>), после чего нажать комбинацию клавиш |
|
|
|
|
<Ctrl>+<G> |
|
|
|
|
|
|
|
|
|
Математическое программное обеспечение. Учебное пособие |
-180- |
|
22.ПЕРЕМЕННЫЕ И ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ОПЕРАЦИИ В MATHCAD
22.11.Стандартные математические функции
|
Окончание табл. 22.2 |
|
|
1 |
2 |
log(z,b) |
Логарифм от z по основанию b, если второй аргумент функции не ука- |
|
зан, логарифм вычисляется по основанию 10 |
sec (z) |
Секанс от z |
sech(z) |
Секанс от z |
sin(z) |
Синус от z |
sinc(z) |
Функция, значение которой вычисляется по формуле sinc(z) = sin(z)/z |
sinh(z) |
Синус гиперболический от z |
tan(z) |
Тангенс от z |
tanh(z) |
Тангенс гиперболический от z |
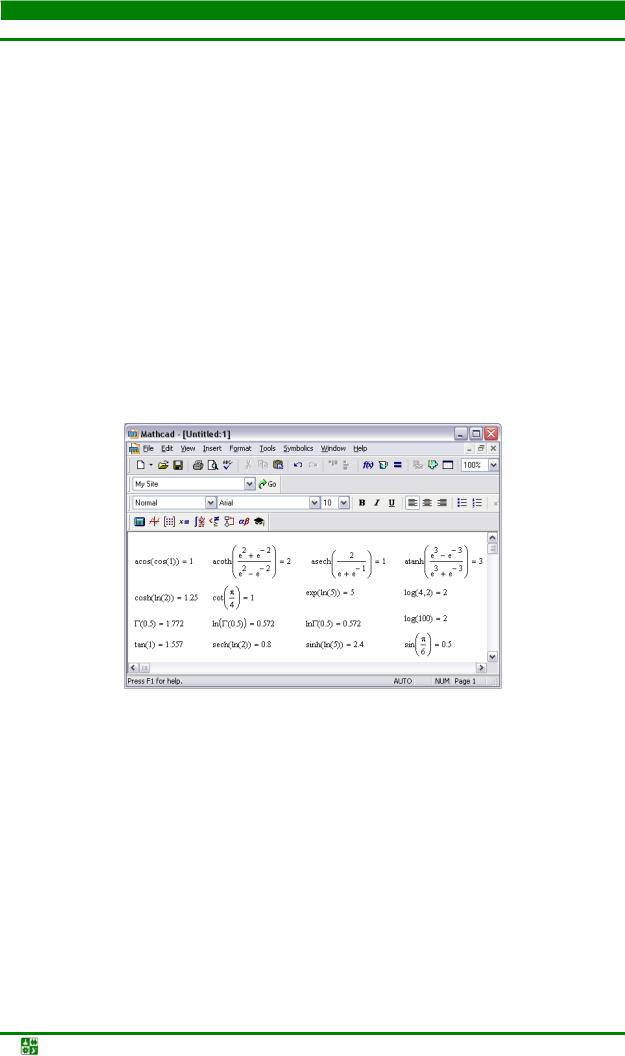
22.12. Математическиефункции
Примеры вызова некоторых функций см. на рис. 22.14.
Рис. 22.14
В рабочих документах MathCad допустимы не только действительные числа, но и комплексные. Они могут быть, в частности, аргументом (или аргументами) для большинства стандартных математических функций. Кроме того, в MathCad есть функции, предназначенные для работы именно с комплексными числами, причем в некоторых случаях возвращаемое функцией значение, в силу ее определения в MathCad, несколько отличается от того, которое можно было бы ожидать исходя из общематематических представлений. Например, функцией signum( ) в качестве значения возвращается в общем случае комплексное число, равное отношению числа-аргумента функции к модулю этого аргумента. Если аргумент у функции нулевой, функцией возвращается значение 1. Таким образом, для действительного аргумента функция возвращает его знак. В некотором родстве к ней (если так можно
Математическое программное обеспечение. Учебное пособие |
-181- |
22.ПЕРЕМЕННЫЕ И ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ОПЕРАЦИИ В MATHCAD
22.12.Математические функции
сказать о функции) находится функция csgn ( ). Однако возвращаемое этой функцией значение всегда действительно. Алгоритм его вычисления довольно замысловат. Функцией возвращается знак действительной части аргумента. Если число мнимое (т. е. действительная часть равна нулю), функция возвращает знак мнимой части аргумента. Для нулевого аргумента значение функции равно нулю. Поэтому для действительных аргументов различие функций signum( ) и csgn( ) состоит лишь в том, что первая для нуля возвр а- щает значение 1, а вторая – 0.
Функции вычисления действительной и мнимой частей комплексного числа в MathCad имеют общепринятые математические названия: Re ( ) для вычисления действительной части и Im( ) – для мнимой. Наконец, аргумент комплексного числа (это угол между действительной осью и вектором, направленным из начала системы координат к точке на комплексной плоскости) можно определить с помощью функции arg ( ). Здесь уместно напомнить, что для задания комплексного числа достаточно знать два параметра. Это могут быть действительная и мнимая части комплексного числа либо его модуль и аргумент. Модуль комплексного числа можно вычислить, заключив число в прямые скобки.
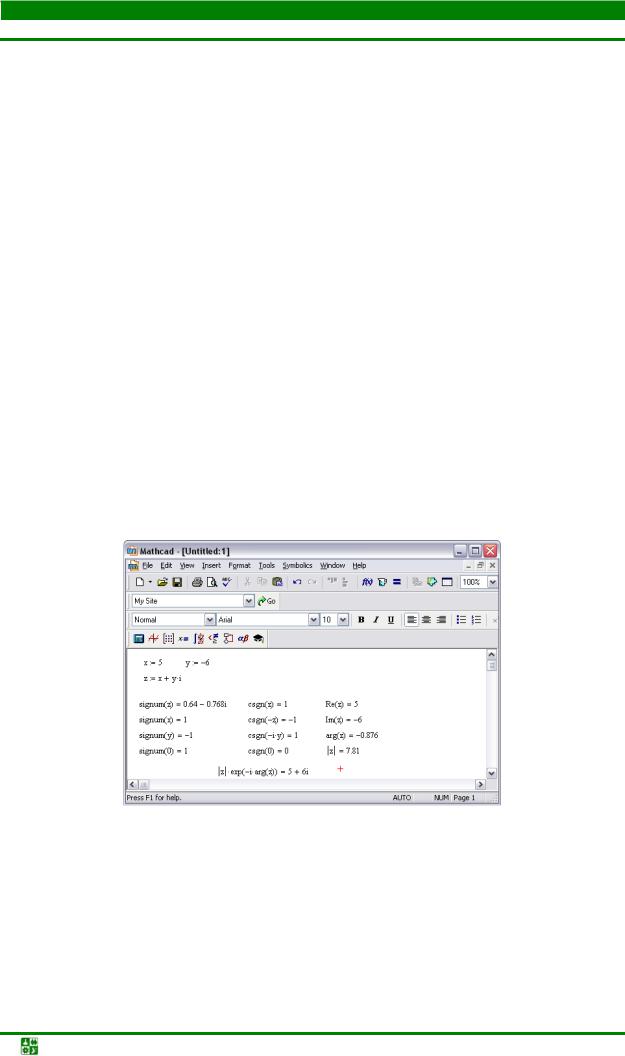
22.13. Работа с комплексными числами
Пример функций с комплексными аргументами см. на рис. 22.15.
Рис. 22.15
22.14. Функции округления численных значений
Группа функций MathCAD, предназначенная для преобразования и округления численных значений, приведена в табл. 22.3. Эти функции собраны в категории Truncation and Round Off диалогового окна вставки функций
Insert Function.
Математическое программное обеспечение. Учебное пособие |
-182- |
22.ПЕРЕМЕННЫЕ И ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ОПЕРАЦИИ В MATHCAD
22.14.Функции округления численных значений
Таблица 22.3
Функция |
Описание |
Ceil(x, у) |
Функцией в качестве значения возвращается наименьшее |
|
кратное числа у, не меньшее числа х |
ceil(x) |
Функцией возвращается наименьшее целое число, которое |
|
больше либо равно х |
Floor(x, у) |
Возвращается наибольшее кратное у, не превышающее х |
floor(х) |
Значением функции является наибольшее возможное целое |
|
число, не превышающее х |
Round(x,у) |
Значение х округляется до ближайшего числа, кратного вто- |
|
рому аргументу функции у. Это значение и возвращается |
|
функцией, при этом значение переменной х не меняется |
round(x,n) |
Число х округляется до n знаков после десятичной точки. Если |
|
второй аргумент функции не указан, то округление выполня- |
|
ется до целочисленного значения. При отрицательном значе- |
|
нии n абсолютное значение второго аргумента определяет ко- |
|
личество разрядов округления в целой части числа |
Trunc(х,у) |
Функцией в качестве значения возвращается результат умно- |
|
жения второго аргумента функции (т. е. у) на целую часть от- |
|
ношения первого аргумента (т. е. х) ко второму |
trunc(х) |
Функцией возвращается целая часть числа х |
22.15. Символьный результат
При попытке вычислить значение функции в символьном виде, т. е. когда аргументами указаны не числа, а символы (названия переменных, которым не присвоены численные значения) с помощью ввода знака равенства после названия функции, результат будет негативным. Однако сделать это можно, если вместо знака равенства ввести оператор вычисления символьного значения (стрелка вправо). Причем в качестве аргументов можно указывать не только отдельные названия, но и целые выражения.
Математическое программное обеспечение. Учебное пособие |
-183- |