Кузнецовой Теория электрических цепей часть 2

представляет собой комплексную величину k-й гармоники

A&	= A e jψk ,	(1.11)
k	k

где Ak = 2 F (kω1 ) .

T

Совокупность амплитуд всех гармоник данной функции может рассматриваться как дискретный спектр этой функции. Его можно представить на графике в виде отрезков вертикальных линий, пропорциональных значениям амплитуд, аналогично для значений начальных фаз каждой гармоники. По оси абсцисс откладываем значения, равные частотам гармоник. Для каждой частоты гармоник откладываем от оси абсцисс параллельно оси ординат отрезки, длины которых равны амплитудам Akm или начальным фазам ψk гармоник. При этом Akm > 0, а ψk может быть как положительным, так и отрицательным. Такие характеристики носят название дискретных спектров или дискретных частотных характеристик – соответственно амплитудно-частотной и фазочастотной.

При построении спектра периодического сигнала по оси абсцисс откладывают кратные основной частоте значения частот гармонических составляющих. Обратим внимание на то, что чем больше период функции f(t), тем плотнее расположены спектральные линии и соответственно меньше значения амплитуд гармонических составляющих. Разумеется, в конкретных случаях те или иные частотные составляющие спектра сигнала могут отсутствовать, но составляющих, частота которых не кратна основной частоте, спектр содержать не может.

Пример. Определим спектр периодической последовательности прямоугольных импульсов амплитуды F0 с длительностью, равной половине периода, T/2 (рис. 1.2, а). Аналитическое выражение временной зависимости рассматриваемого сигнала в этот период имеет вид

= F0 f (t)

0

при 0 < t < T , 2

при T < t < 3 T. 2 2

11

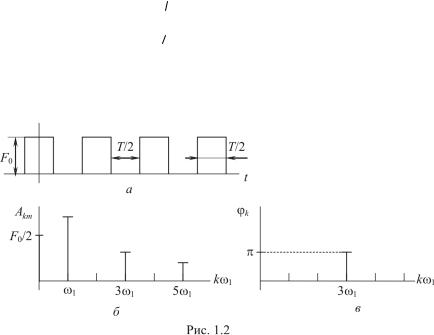
Если за начало отсчета выбрать начало координат, то функция будет обладать четной симметрией и содержать только косинусные составляющие с коэффициентами Akm. Определим амплитуду k-й гармоники:

	2 −T 4				2F		kπ
A =		∫	F cos kω tdt =		0	sin		.
	T				kπ
km			0	1		2
		T 4

Отсюда

A =

2F0

; A = −

1

2F0

; A =

1

2F0

; A = F ; A = A = 0; B = 0.

π

3 π

5 π

1m

3m

5m

0 0 2m 4m

km

НайденныекоэффициентыпозволяютзаписатьразложениеФурье:

f (t) =	F0	+	2F0	(cos ω t −	1	cos3ω t +	1	cos5ω t).
2			π	1	3	1	5	1

Коэффициенты ряда принимают следующие значения:

	A =	F0	; A =	2F0	(k =1, 2, 3K);
		2		kπ
	0		km

ψk = 0 (k = 4n +1, n = 0, 1, 2, K); ψk = π (k = 4n −1, n =1, 2, 3, K).

Спектры амплитуд и фаз рассматриваемой функции показаны на рис. 1.2, б и в.

12

1.1. МАКСИМАЛЬНОЕ, СРЕДНЕЕ, ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЯ НЕСИНУСОИДАЛЬНОЙ ФУНКЦИИ

Максимальное значение несинусоидальной периодической функции – наибольшее по модулю значение функции запериод.

Среднее по модулю значение определяется по формуле

		T	∫
F	=	1	T	f (t)	dt .	(1.12)
ср
			0

Если кривая f(t) симметрична относительно оси абсцисс и в течение половины периода ни разу не изменила знака, то среднее по модулю значение равно среднему значению за половину периода:

2 T2

Fср = T ∫0 f (t)dt ,

причем начало отсчета времени в этом выражении должно быть выбрано так, чтобы f(0) = 0. Если за весь период функция ни разу не изменила знака, то среднее по модулю значение равно постоянной составляющей.

При несинусоидальных периодических воздействиях, как и при синусоидальных, обычно под значением ЭДС, тока или напряжения понимают действующее значение.

Действующее значение несинусоидальной функции – это среднеквадратическое значение за период мгновенного значения функции

1 T

F = ∫ f 2 (t)dt . (1.13)

T 0

Определим действующее значение на примере напряжения. Пусть

u(t) =U0 +U1m sin (ω1t + ψ1 ) +U2m sin (2ω1t + ψ2 ) +K,

тогда

13

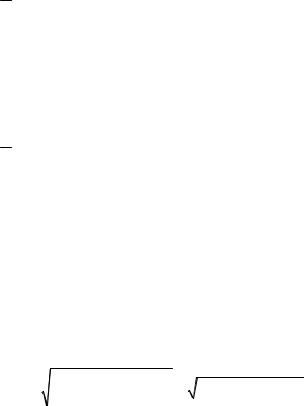
u2 (t) = U	+U	1m	sin (ω t + ψ ) +U	2m	sin (2ω t + ψ	2	) +K	2	=
0			1 1		1
∞				∞
=U02 + ∑Ukm2 sin2 (kω1t + ψk ) +U0 ∑Ukm sin (kω1t + ψk ) +									(1.14)
k =1				k =1

∞

+ ∑ U pmUqm sin ( pω1t + ψp )sin (qω1t + ψq ).

p=1, q=1, p≠q

Рассмотрим интегралы от каждого из слагаемых в отдельности:

T

1. T1 ∫0 U02 dt =U02 – это квадрат постоянной составляющей на-

пряжения.

	1	T	2
2.		∫Ukm2	sin2 (kω1t + ψk )dt =	Ukm	=Uk2 , так как этот интеграл
	T
		0	2

по определению равен квадрату действующего значения Uk гармонической составляющей напряжения k-й гармоники.

T

3. T1 ∫0 U0Ukm sin (kω1t + ψk )dt = 0 , так как интеграл от синусои-

дальной величины за целое число периодов равен нулю.

	1	T	1	T	U pmUqm
4.		∫U pmUqm sin ( pω1t + ψp )sin (qω1t + ψq )dt =		∫		×
	T		T		2
		0		0

×[cos( pω1t + ψp − qω1t −ψq ) −cos ( pω1t + ψp + qω1t + ψq )]dt = 0 ,

где p ≠ q; подынтегральное выражение является разностью двух косинусоидальных функций, интеграл каждой из которых за целое число периодов равен нулю.

Таким образом, действующее значение периодического несинусоидального напряжения

U = U02 +	U12m	+	U22m	+K = U02 +U12 +U	22 +K ,	(1.15)
2		2

т.е. действующее значение периодического несинусоидального напряжения равно корню квадратному из суммы квадратов постоянной

14

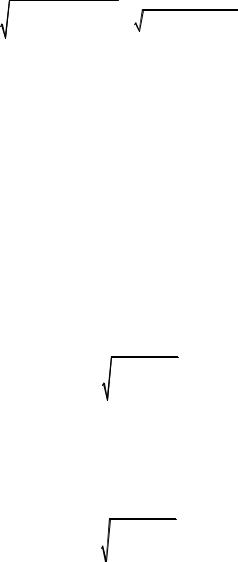
составляющей и квадратов действующих значений всех гармонических составляющих. Так же определяется действующее значение периодического несинусоидального тока:

			I 2		I 2
I =	I 2	+	1m	+	2m	+ K = I 2	+ I 2	+ I 2	+ K .	(1.16)
	0		2		2	0	1	2

Аналогичным образом определяется действующее значение любой другой периодической несинусоидальной величины.

Несинусоидальные токи и напряжения измеряют приборами различных систем. Приборы электромагнитной, электродинамической и тепловой систем реагируют на действующее значение, магнитоэлектрические приборы с выпрямителем – на среднее значение, магнитоэлектрические без выпрямителя – на постоянную составляющую.

1.2. КОЭФФИЦИЕНТЫ, ХАРАКТЕРИЗУЮЩИЕ ПЕРИОДИЧЕСКИЕ НЕСИНУСОИДАЛЬНЫЕ ФУНКЦИИ

В электротехнике при оценке несинусоидальных периодических кривых пользуются коэффициентом формы кривой kф, коэффициентом амплитуды kа и коэффициентом искажения kи.

Коэффициент формы определяется как отношение действующего значения функции к среднему значению функции, взятой помодулю:

1

T

∫ f 2 (t)dt

=

F

=

T

k

0

.

(1.17)

ф

F

1

T

∫

ср

f (t)

dt

T

0

Коэффициент амплитуды определяется как отношение максимального значения функции к ее действующему значению:

k	а	=	Fm	=			Fm	.	(1.18)
			F			1	T
							∫ f 2 (t)dt
						T
							0

15

Для синусоиды kф =		π	=1,11; kа = 2 =1, 41.
		2
2

Коэффициент искажения определяется как отношение действующего значения основной (первой) гармоники к действующему значению всей функции:

kи =			F1	.	(1.19)
			T
1
			∫ f 2 (t)dt
		T
			0

Для синусоиды kи =1 .

В электронике и радиотехнике для оценки искажений пользуются коэффициентом гармоник, определяемым как отношение действующего значения высших гармоник к действующему значению основной гармоники:

		1	∞
	kг =		∑ Fk2 .	(1.20)
		F1
			k =2

1.3. АКТИВНАЯ И ПОЛНАЯ МОЩНОСТЬ НЕСИНУСОИДАЛЬНОГО ТОКА

Выражение мгновенной мощности

p(t) = u(t)i(t)

(1.21)

справедливо для токов и напряжений с любой формой кривой.

Под активной мощностью несинусоидального тока понимают, как и в цепях синусоидального тока, среднее значение мгновенной мощности за период первой гармоники:

1 T

P = ∫uidt . (1.22)

T 0

Если представить напряжение и ток рядами Фурье: u =U0 +U1m sin (ω1t + ψu1 ) +U2m sin (2ω1t + ψu2 ) +K, i = I0 + I1m sin (ω1t + ψi1 ) + I2m sin (2ω1t + ψi2 ) +K,

16

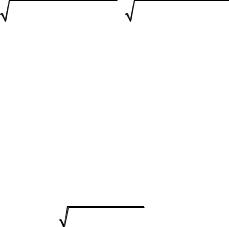
то активная мощность будет представлена суммой интегралов тех же четырех типов, что и при рассмотрении действующего значения периодического несинусоидального тока.

Таким образом,

P = P + P +K+ P +K=U				I	0	+U I cos ϕ +
0 1		k	0			1 1 1	(1.23)
+K+Uk Ik	cos ϕk	+K,

где ϕk = ψuk −ψik .

Активная мощность при периодических несинусоидальных токах и напряжениях равна сумме активных мощностей постоянной (мощности постоянного тока) и всех гармонических составляющих тока и напряжения.

Реактивной мощностью периодических несинусоидальных токов можно условно считать величину, равную сумме реактивных мощностей отдельных гармоник:

Q = Q1 +Q2 +K=U1I1 sin ϕ1 +U2 I2 sin ϕ2 +K.

(1.24)

По аналогии с синусоидальными токами вводят понятие полной мощности, определяемой как произведение действующих значений токов и напряжений:

S =UI = U 2	+U 2	+U 2	+K	I 2	+ I 2	+ I 2	+K.	(1.25)
0	1	2		0	1	2

В отличие от цепи синусоидального тока

S 2 ≠ P2 +Q2 , S 2 ≥ P2 +Q2

(равенство имеет место при активной нагрузке). Это объясняется тем, что полная мощность содержит все гармоники, в том числе и произведения токов и напряжений разной частоты, поэтому для несинусоидальных токов квадрат полной мощности обычно больше суммы квадратов активной и реактивной мощностей.

Мощность искажения

T = S 2 − P2 −Q2

(1.26)

характеризуетстепеньразличиявформахкривыхнапряженияu итокаi.

17

По аналогии с синусоидальными функциями отношение активной мощности при несинусоидальных токах к полной мощности ус-

ловно называют коэффициентом мощности λ.

				∞
	P			∑ Pk
λ =		=		k =0
					.	(1.27)
	S		∞	∞
			∑Uk2 ∑ Ik2
			k =0	k =0

λ =1, если цепь обладает только одним активным сопротивлением, во всех остальных случаях λ <1 .

Пусть напряжение синусоидально, а ток несинусоидален. В этом случае

P =U1I1 cos ϕ1 =UI1 cos ϕ1 .

Действующее значение тока

I = I02 + I12 + I22 +K+ Ik2 +K > I1 .

Следовательно,

λ = UI1 cos ϕ1 = I1 cos ϕ1 = kи cos ϕ1 , (kи <1).

UI I

Таким образом, появление высших гармоник в кривых напряжения и тока приводит к снижению коэффициента мощности по сравнению со случаем, когда ток и напряжение при тех же действующих значениях синусоидальны. Следовательно, хотя бы в этом отношении появление высших гармоник нежелательно. Поэтому стремятся конструировать генераторы переменного тока так, чтобы кривая ЭДС в них была по возможности близка к синусоиде.

1.4. РАСЧЕТ ЛИНЕЙНОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПРИНЕСИНУСОИДАЛЬНЫХПЕРИОДИЧЕСКИХВОЗДЕЙСТВИЯХ

Если в линейной электрической цепи действует один или несколько источников несинусоидальных периодических ЭДС и токов, то расчет такой цепи ведется в три этапа.

18

1.Разложение ЭДС и токов источников на постоянную и синусоидальные составляющие, т.е. в ряд Фурье. Часто встречающиеся

вэлектротехнике периодические кривые и их разложение в ряд Фурье приведены в учебниках по ТОЭ и в математических и электротехнических справочниках.

2.Применение принципа наложения, согласно которому мгновенное значение тока любой ветви (напряжения на любом участке) равно сумме мгновенных значений токов (напряжений) отдельных гармоник, и расчет токов и напряжений в цепи для каждой гармоники

вотдельности.

3.Совместное рассмотрение решений, полученных для каждой из составляющих.

Рассмотрим подробнее второй этап, представляющий собой основную часть расчета.

Пусть несинусоидальная ЭДС представлена в виде суммы постоянной и синусоидальных составляющих,

e(t) = E0 + E1m sin (ω1t + ψ1 ) + E2m sin (2ω1t + ψ2 ) ,

тогда согласно принципу наложения источник несинусоидальной ЭДС можно рассматривать как последовательное соединение источника постоянной ЭДС и источников синусоидальных ЭДС с различными кратными частотами (рис. 1.3):

e0 = E0 , e1 = E1m sin (ω1t + ψ1 ) , e2						= E2m sin (2ω1t + ψ2 ) .
									e2
	e(t)					e
				E0			1

Рис. 1.3

Если заданы токи несинусоидальных источников, то подход к решению задачи остается таким же. Источники несинусоидального тока можно представить в виде параллельного соединения нескольких источников, синусоидальный ток каждого из которых равен соответствующей составляющей несинусоидального тока (рис. 1.4).

19

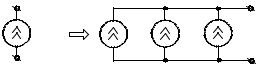
j(t)	j1	j2
J0
Рис. 1.4

Далее можно определить токи и напряжения, возникающие от действия постоянных составляющих ЭДС и задающих токов источников, после этого – токи и напряжения от действия первых гармоник, затем от вторых гармоник и т.д. Мгновенное значение тока или напряжения в цепи будет равно сумме мгновенных значений составляющих токов или напряжений от действия каждого из источников. Если, например, в какой-либо ветви токи, создаваемые ЭДС E0, e1, e2, соответственно равны I0, i1, i2, то полный ток

i = I0 +i1 +i2 .

Таким образом, расчет линейной цепи с несинусоидальными воздействиями сводится к решению n задач с синусоидальными ЭДС (n – количество синусоидальных составляющих ЭДС различных частот) и одной задачи с постоянной ЭДС. При этом необходимо помнить, что напряжение на индуктивности в цепях постоянного тока равно нулю

( X L0 = 0 ), а постоянный ток через емкость не проходит ( X С0		= ∞ ).
Следует также учитывать, что индуктивное сопротивление X Lk		растет
прямо пропорционально частоте, поэтому для k-й гармоники
X L	= kω1L = kX L .	(1.28)
k	1

Емкостное сопротивление уменьшается с ростом частоты, поэтому для k-й гармоники X Ck вk раз меньше, чем дляпервой гармоники:

		=	1	=	X C
X C					1	.	(1.29)
			kω1C
	k				k

Поскольку каждая составляющая в (1.3) является либо постоянной, либо синусоидальной функцией времени, то для расчета каждой

20