Корреляционная зависимость. Выборочный коэффициент корреляции. Линейная корреляция. Выборочное линейное уравнение регрессии

Пусть имеется система двух случайных величин Х и Y, связанная с некоторым случайным экспериментом. В результате каждого такого эксперимента обе величины принимают некоторые числовые значения. В какой связи могут находиться эти величины? Самая сильная связь − функциональная: Y=g(X) . В этом случае, если известно, что в результате эксперимента с.в. Х приняла некоторое значение х, то можно точно сказать, что случайная величина Y при этом приняла строго определенное значение y=g(x) . Мы уже приводили соответствующий пример, когда месячная заработная плата сотрудника фирмы составляет 1% от месячной прибыли фирмы. В этом случае случайные величины Х (месячная прибыль фирмы ) и Y (месячная зарплата сотрудника) связаны функциональной зависимостью: Y=0.01∙X . Однако чаще всего приходится сталкиваться с более сложной зависимостью, когда значение х, принятое в результате эксперимента случайной величиной Х не определяет однозначно значение у, принимаемое случайной величиной Y в этом же эксперименте. Это бывает, когда на фактор Y кроме фактора Х влияют и многие (или немногие) другие случайные факторы. В этом случае говорят не о функциональной, а о стохастической (или вероятностной) зависимости Х и Y, когда принятому величиной Х значению соответствует не одно, а множество возможных значений переменной Y, причем нельзя заранее сказать, какое из них будет принято. Такова, например, связь между количеством осадков и урожаем, между толщиной снегового покрова и и объемом стока последующего половодья, цена товара и величина спроса на нее, объем производства и прибыль фирмы, располагаемый доход и объем личного потребления, инфляция и безработица и т.д. . В случае стохастической зависимости каждому значению х, принятому величиной Х, соответствует свое определенное условное (при условии, что величина Х приняла данное значение х) распределение (закон распределения или функция распределения) случайной величины Y. Если мы вычислим среднее значение (т.е. математическое ожидание) этой величины Y, то оно будет называться условным математическим ожиданием с.в. Y (при условии, что с.в. Х приняла данное значение х) и обозначается M_x(Y). Аналогично определяется условное математическое ожиданием с.в. Х (при условии, что с.в. Y приняла данное значение у) и обозначается M_у(Х). Итак, каждому возможному значению х величины Х однозначно соответствует число, равное условному математическому ожиданию M_x(Y) величины Y, а каждому возможному значению у величины Y однозначно соответствует число, равное условному математическому ожиданию M_у(Х). величины Х. Корреляционной зависимостью величинами Х и Y называется функциональная зависимость между значениями одной из них и условным математическим ожидаем другой. Такая зависимость показывает, как в среднем зависят значения одной из них от значений, принятых другой. Корреляционная зависимость может быть записана в виде M_x(Y)=f(x) , M_у(Х)=g(y) . Рассмотрим соответствующие функции (уравнения)

у=f(x) и х=g(y) .

Эти функции (или уравнения) называются функциями (или уравнениями) регрессии соответственно Y на Х и Х на Y. Графики этих функций называются линиями регрессии. Они показывают, как меняется среднее значение одной случайной величины в зависимости от того, какое значение приняла в эксперименте другая случайная величина.

На практике важную роль играет так называемая линейная корреляция. Корреляционная зависимость между величинами Х и Y называется линейной корреляцией, если обе функции регрессии f(x) и g(y) являются линейными функциями (т.е. функциями вида f(x)=a∙x+b, g(y)=c∙y+d). В этом случае обе линии регрессии являются прямыми, которые называются прямыми регрессии.

Основной задачей корреляционного анализа является выявление наличия или отсутствия связи между величинами Х и Y, а также количественная оценка тесноты этой связи. Цель же регрессионного анализа – записать выявленную связь в виде уравнения (уравнения регрессии).

Пример. Пусть с.в. Х и Y независимы. Обозначим их математические ожидания М(Х)=а и M(Y)=b. Пусть с.в. Х приняла в эксперименте некоторое значение х. Поскольку с.в. Х и Y независимы, то условное распределение с.в. Y при этом не изменилось, а значит не изменилось и ее математическое ожидание (оно вычисляется по распределению – закону или функции распределения). Таким образом, M_x(Y)= M(Y)=b. Аналогично, M_у(Х)= М(Х)=а. Таким образом, функции регрессии у=b и х=a, т.е. для независимых случайных величин функции регрессии являются постоянными (см. рисунок).

Если функции регрессии являются постоянными, то говорят, что между случайными величинами Х и Y корреляционная связь отсутствует.

Пример. Рассмотрим теперь другой крайний случай – случай функциональной зависимости случайных величин. Пусть, например, с.в. Y линейно зависит от с.в. Х : Y = k ∙X + b. Пусть с.в. Х приняла в эксперименте некоторое фиксированное значение х. Поскольку с.в. Х и Y связаны функционально уравнением Y = k ∙X+b, то величина Y может принять теперь только одно фиксированное значение у = k ∙х+b . Таким образом, с.в. Y становится при этом дискретной случайной величиной, которое может принять единственное значение у = k ∙х+b с вероятностью единица. Тогда по определению (или по первому свойству математического ожидания) математическое ожидание такой случайной величины равно ее единственному значению у = k∙х+b . Таким образом, условное математическое ожидание с.в. Y (при условии, что с.в. Х приняла конкретное значение х) M_x(Y) = k∙х+b, т.е. в данном случае f(x) = k∙х+b. Поэтому уравнение регрессии Y на Х имеет вид

у = k ∙х + b .

Если из уравнения связи случайных величин Y = k ∙X+b выразить Х через Y : , то можно считать, что с.в.Х является также линейной функцией от с.в. Y . Поэтому по аналогии получаем, что уравнение регрессии Х на Y имеет вид

.

Таким образом, в случае линейной зависимости случайных величин линиями регрессии являются прямые, уравнения которых совпадают с уравнением линейной зависимости самих случайных величин.

Это правило справедливо и в общем случае любой (не только линейной) функциональной зависимости случайных величин: в случае функциональной зависимости случайных величин линиями регрессии являются кривые, уравнения которых совпадают с уравнением функциональной зависимости самих случайных величин.

Ранее для количественной характеристики тесноты связи между случайными величинами Х на Y был введен коэффициент корреляции

.

Напомним, что если величины Х и Y независимы, то коэффициент корреляции r_XY = 0, а если r_XY = ±1, то случайные величины связаны некоторой линейной функциональной зависимостью: Y=aX+b. Таким образом, коэффициент корреляции измеряет силу (тесноту) линейной связи между Х и Y. В математической статистике нам не известны законы распределения с.в. Х и Y, поэтому мы не можем найти точное значение коэффициента корреляции для оценки тесноты линейной связи случайных величин. Нам известны только их выборки, по которым необходимо получить хотя бы приближенную оценку коэффициента корреляции. Пусть для получения выборок произведено n случайных экспериментов. Допустим, в первом эксперименте случайные величины Х и Y приняли значения х₁ и у₁ соответственно, во втором эксперименте х₂ и у₂ , … , в последнем х_n и у_n . Таким образом, получены две выборки { х₁, х₂ , … , х_n } и { у₁ , у₂ , … , у_n } случайных величин Х и Y соответственно. Заметим, что некоторые варианты в выборках могут повторяться. Для получения по ним оценки коэффициента корреляция было бы естественно в формуле для этого коэффициента заменить входящие в нее математические ожидания и средние квадратические отклонения их выборочными характеристиками – выборочными средними и выборочными средними квадратическими отклонениями:

.

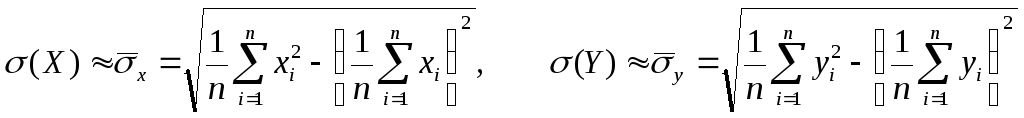В результате такой замены получается следующая формула для так называемого выборочного коэффициента корреляции :

или более подробно

.

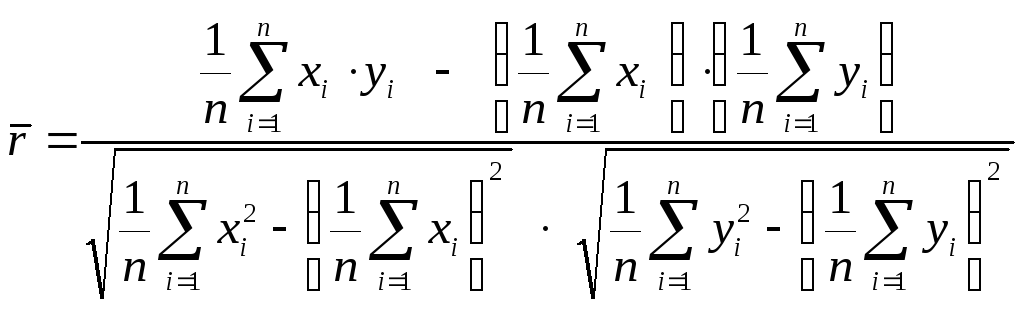Умножив числитель и знаменатель на n, можно несколько упростить формулу для выборочного коэффициента корреляции :

.

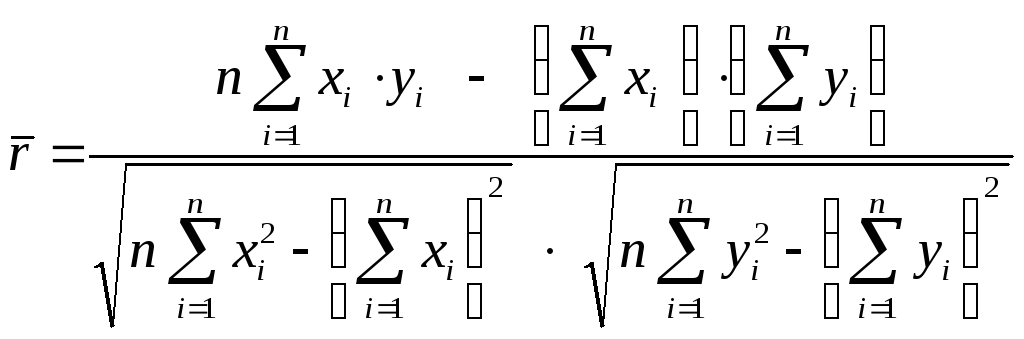Так как выборочный коэффициент корреляции вычисляется по данным выборки, то он, в отличие от истинного коэффициента корреляцииr (или, как говорят , генерального коэффициента корреляции), является величиной случайной. С какой же точностью выборочный коэффициент корреляции приближает генеральный? Если выборка имеет достаточно большой объем и хорошо представляет генеральную совокупность (т.е. репрезентативна), то заключение о тесноте линейной зависимости между величинамиХ и Y, полученное при анализе вычисленного выборочного коэффициента корреляции , в известной степени может быть распространено и на саму генеральную совокупность. Например, если объем выборки достаточно велик (n ≥ 50 ) и случайные величины Х и Y распределены нормально (это можно определить по критерию χ² Пирсона) , то можно воспользоваться формулой:

.

Допустим, что выборочный коэффициент корреляции показал нам, что для величин Х и Y существует линейная функция, которая достаточно хорошо описывает зависимость между ними. Это дает нам уверенность, что корреляция величин Х и Y близка к линейной, а линии регрессии близки к прямым линиям. Как же по выборке найти конкретный вид этой линейной функции, т.е. определить ее параметры?

Напомним, что для получения выборок произведено n случайных экспериментов. В первом эксперименте случайные величины Х и Y приняли значения х₁ и у₁ соответственно, во втором эксперименте х₂ и у₂ , … , в последнем х_n и у_n . Таким образом, получены две выборки { х₁, х₂ , … , х_n } и { у₁ , у₂ , … , у_n } случайных величин Х и Y соответственно (некоторые варианты в выборках могут повторяться). Будем искать выборочное (т.е. полученное по выборке) уравнение прямой линии регрессии Y на Х в виде

.

Угловой коэффициент этой прямой обозначаетсяназываетсявыборочным коэффициентом регрессии Y на Х .

В результате произведенной выборки мы получили такие значения двумерной случайной величины (двумерного случайного вектора) {X,Y}:

(х₁,у₁), (х₂,у₂), … , (х_n,у_n).

Н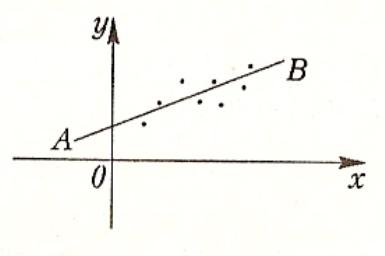анесем на координатную плоскостьxOy точки с этими координатами (х₁,у₁), (х₂,у₂), … , (х_n,у_n). Такое графическое изображение выборки называется полем корреляции. В общем случае эти точки не будут точно располагаться на одной прямой, но, если установлена связь величин, близкая к линейной, то они будут близки к этому. Нужно найти уравнение такой прямой АВ, чтобы нанесенные точки располагались к ней как можно ближе (рисунок). Это уравнение и даст нам выборочное уравнение регрессии . Применяемый далее метод нахождения параметровρ и b указанной прямой называется методом наименьших квадратов. Согласно этому методу составим сумму квадратов (так удобнее) отклонений (отклонение рассматривается по вертикальному направлению) нанесенных точек от прямой с уравнением . Это будет функция двух переменных, зависящая от параметровρ и b, следующего вида:

.

Теперь нужно найти такие параметры ρ и b , при которых эта сумма была бы минимальной. Это приводит к классической задаче математического анализа на отыскание точки минимума выписанной функции . По правилу нахождения экстремумов функции двух переменных находим ее частные производные

,

и приравниваем их нулю. В результате получается следующая система линейных уравнений для искомых параметров ρ и b :

.

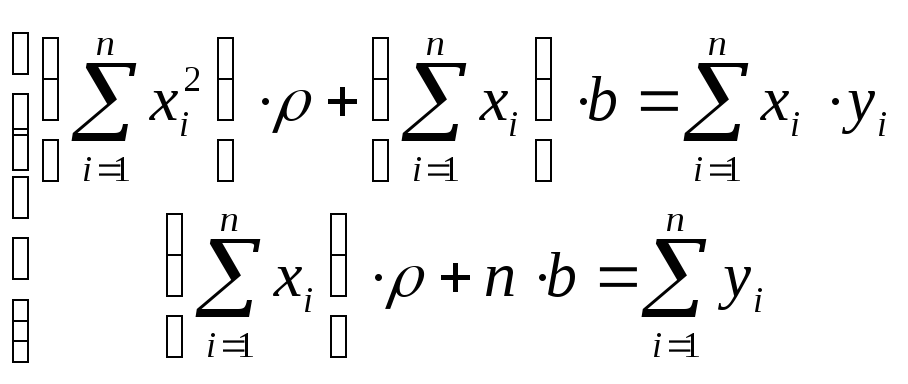Разделив обе части уравнений системы на n, получим

.

Из второго уравнения можно сразу выразить b :

.

Подставляя теперь это в первое уравнение и выражая , получим

или .

Таким образом, для выборочного уравнения регрессии Y на Х

получены следующие формулы выборочного коэффициента регрессии величиныY на Х и параметра b :

, .

Сравнивая полученное выражение для с выражением для выборочного коэффициента корреляции , получим выражение выборочного коэффициента регрессии через выборочный коэффициент корреляции :

.

Подставляя в уравнение регрессии, легко получить запись выборочного линейного уравнения регрессииY на Х в принятой в математической статистике форме :

или, подставляя выражение через выборочный коэффициент корреляции :

.

Аналогично, выборочное линейное уравнение регрессии Х на Y имеет вид:

.

Напомним формулы для входящих в эти уравнения выборочных характеристик через данные выборки:

,

.

Из уравнений выборочной линейной регрессии видно, что знак выборочного коэффициента корреляции определяет направление связи величинХ и Y. Если , то связь прямая : с возрастанием (убыванием) значения одной из величин растет (убывает) и среднее значение другой величины. Если же, то связь обратная : с возрастанием (убыванием) значения одной из величин убывает (растет) и среднее значение другой величины.

Пример. В результате эксперимента были получены 6 пар соответствующих друг другу значений переменных величин Х и Y :

Х	0	1	2	3	4	5
Y	5.1	4.7	4.4	4.5	4.3	4.0

Найти выборочный коэффициент корреляции и выборочное линейное уравнение регрессии Y на Х .

Решение. Для выборочного коэффициента корреляции используем формулу . Вычислим входящие в эту формулу выборочные величины, используя объем выборкиn=6 и значения вариант, данные в таблице:

.

Тогда . Выборочный коэффициент корреляции оказался близок к( −1), что говорит о наличии достаточно хорошей линейной (обратной) связи переменных Х и Y. Поэтому имеет смысл искать выборочное уравнение именно линейной регрессии . Подставляя полученные значения, получаем . Раскрывая скобки и приводя подобные, получим следующий видвыборочного линейного уравнения регрессии Y на Х : .

Зная вид выборочного линейного уравнения регрессии Y на Х можно прогнозировать приближенные значения величины Y при тех значениях величины Х, которые не попали в выборку. Полагая в полученном уравнении , например, х=6, получим прогнозируемое значение величины Y : .

Пример. С помощью выборочного коэффициента корреляции оцените тесноту (линейной) связи между стажем работы (в годах) рабочих и выработкой за смену (в чел.-час.) по данным следующей выборки:

Х − стаж	1	3	5	7	9
Y − выработка	10	12	16	15	20

Найдите линейное уравнение этой связи.