Графическое изображение статистического распределения выборки

Для большей наглядности статистическое распределение выборки обычно изображают в виде так называемых полигона и гистограммы. Полигон часто (или относительных частот) строят в основном для дискретного статистического ряда. Пусть дано статистическое распределение выборки для частот или относительных частот:

xi	x1	x2	…	xk
ni	n1	n2	…	nk

xi	x1	x2	…	xk
wi	w1	w2	…	wk

Полигоном частот называется ломаная, соединяющая точки с координатами (x₁, n₁), (x₂, n₂), … ,(x_k, n_k). При этом варианты х₁, х₂, … , х_k откладываются на оси абсцисс, а частоты n₁, n₂, … , n_k на оси ординат.

Полигоном относительных частот называется ломаная, соединяющая точки с координатами (x₁, w₁), (x₂, w₂), … ,(x_k, w_k).

Для непрерывных с.в. , статистическое распределение выборки которых представлено в виде интервального статистического ряда

xi	[a0,a1)	[a1,a2)	…	[ak−1,ak]
ni	n1	n2	…	nk

xi	[a0,a1)	[a1,a2)	…	[ak−1,ak]
wi	w1	w2	…	wk

тоже можно строить полигоны частот и относительных частот, если в качестве чисел х₁, … , х_k взять середины интервалов: , … ,. Но для интервальных статистических рядов более употребительна так называемая гистограмма.

Пусть дан интервальный статистический ряд для некоторой выборки. Гистограммой частот (относительных частот) называется ступенчатая фигура, состоящая из прямоугольников, в основании которых лежат числовые отрезки длины h : [a₀ , a₁), [a₁ , a₂), … , [a_k-2 , a_k−1), [a_k−1 , а_k], а высоты равны () . Отметим, что площади таких прямоугольников равны соответствующим частотам (относительным частотам), а площадь всей фигуры равна объему выборкиn (равна 1) . Ступенчатая линия, образованная верхними основаниями прямоугольников в гистограмме для относительных частот, является приближением графика плотности вероятности рассматриваемой н.с.в. Х.

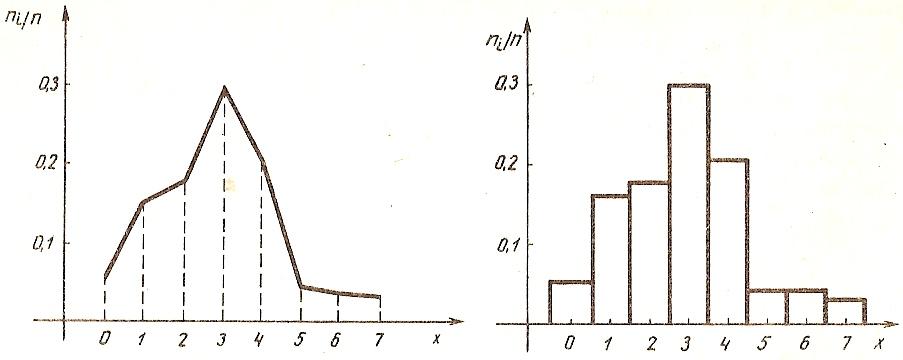
Пример. Построить полигон и гистограмму относительных частот по статистическому распределению выборки :

xi	0	1	2	3	4	5	6	7
ni	4	13	14	24	16	3	3	2

Решение. По данному статистическому ряду частот строим статистический ряд относительных частот. Для это складываем все частоты и получаем, что объем данной выборки n=79. Далее, деля частоты на объем выборки в соответствии с формулой , вычисляем значения относительных частот и оформляем таблицей статистический ряд относительных частот:

xi	0	1	2	3	4	5	6	7
wi= ni /n	0.0506	0.1646	0.1772	0.3038	0.2025	0.0380	0.0380	0.0253

Теперь строим требуемую гистограмму и полигон по описанным выше правилам (рисунки).

Эмпирическая функция распределения

В теории вероятностей универсальной характеристикой случайной величины Х (дискретной и непрерывной) являлась ее функция распределения F(x). Напомним, что для любого числа х эта функция выражала вероятность того, что с.в. Х примет значение, меньшее этого числа Х (т.е. примет значение из интервала (−∞,х) ) : F(x)=Р(X<x). Как по выборке найти приближение к F(x)? Из статистического определения вероятности следует, что при большом числе испытаний n вероятность события приближенно равна его частоте. Пусть n_x обозначает число испытаний (из их общего количества n), в которых с.в. Х приняла значение, меньшее х. Тогда относительная частота события (X<x) в этих n испытаниях по определению W_n(X<x)= n_x /n . Поэтому получаем, что F(x)=Р(X<x) ≈ W_n(X<x)= n_x /n . Таким образом, функция распределения F(x) ≈ n_x /n.

Из сказанного понятно введение следующего определения. Эмпирической функцией распределения (для данной выборки объема n) называется функция, обозначаемая и определяющая для каждого числах относительную частоту события (X<x) в проведенных при получении выборки испытаниях:

,

где n_x обозначает число испытаний (из их общего количества n), в которых с.в. Х приняла значение, меньшее х. Если построено статистическое распределение выборки для частот или относительных частот:

xi	x1	x2	…	xk
ni	n1	n2	…	nk

xi	x1	x2	…	xk
wi	w1	w2	…	wk

то можно конструктивно построить эмпирическую функцию распределения . Для заданного значениях определяем интервал, в который попало это значение: (−∞,х₁] или (х₁, х₂] или (х₂, х₃] или …. или (x_k, +∞) . Если х попадает в первый из этих интервалов, то, очевидно, n_x=0, а потому и . Еслих попадает в последний из этих интервалов, то, очевидно, n_x=n₁+n₂+ … +n_k=n, а потому . Если жех попадает в (х_m , х_m+1] , то, очевидно, n_x=n₁+n₂+ … +n_m , а потому . Выпишем получившийся общий вид эмпирической функции распределения:

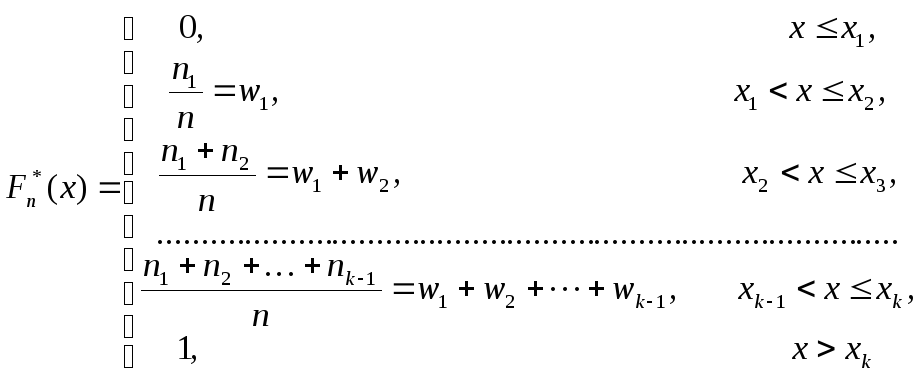
Из сказанного выше следует, что эмпирическая функция распределения является приближением истинной (или, говорят, теоретической) функции распределенияF(x) исследуемой случайной величины Х : ≈ F(x). Строгим обоснованием этого факта служит одна из теорем так называемого закона больших чисел.

Теорема. Функция сходится к функцииF(x) по вероятности. Это означает, что для любого (или, что то же самое,) .

Пример. Пользуясь статистическим рядом относительных частот для выборки объема n=10 :

xi	0	1	2	3	4	5
wi	0.1	0.2	0.1	0.1	0.2	0.3

найти эмпирическую функцию распределения и построить ее график.

Решение. Пользуясь указанным выше общим видом эмпирической функции распределения, получаем:

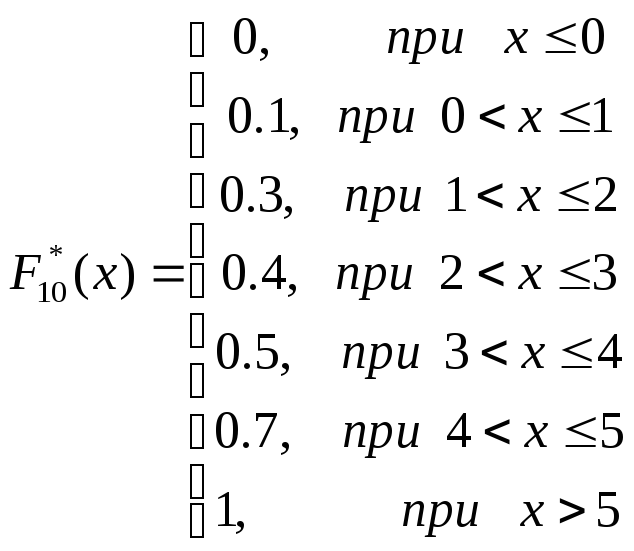
Ниже приведен график этой функции.