Доверительный интервал для математического ожидания нормально распределенной генеральной совокупности при неизвестном среднем квадратическом отклонении

Пусть теперь с.в. Х распределена нормально с параметрами М(Х)=а и σ(Х)= σ, причем оба этих параметра неизвестны. Требуется построить доверительный интервал для математического ожидания, покрывающий параметр а с заданной надежностью γ . Пусть сделана выборка { x₁, x₂, … , x_n } с.в. Х объема n и по ней вычислено выборочное среднее и исправленное среднее квадратическое отклонение

Полученную выборку { x₁, x₂, … , x_n } снова рассматриваем как реализацию системы независимых случайных величин X₁, X₂, … , X_n , каждая из которых тоже имеет нормальное распределение с теми же параметрами а и σ . При этом вычисленное выше выборочное среднее есть реализация случайной величины

,

а выборочное исправленное среднее квадратическое отклонение s есть реализация случайной величины S_n, которая соответствующим образом выражается через случайные величины X₁, X₂, … , X_n и введенную выше случайную величину :

.

Тогда оказывается, что случайная величина Т_n , выражающаяся через введенные случайные величины иS_n по формуле

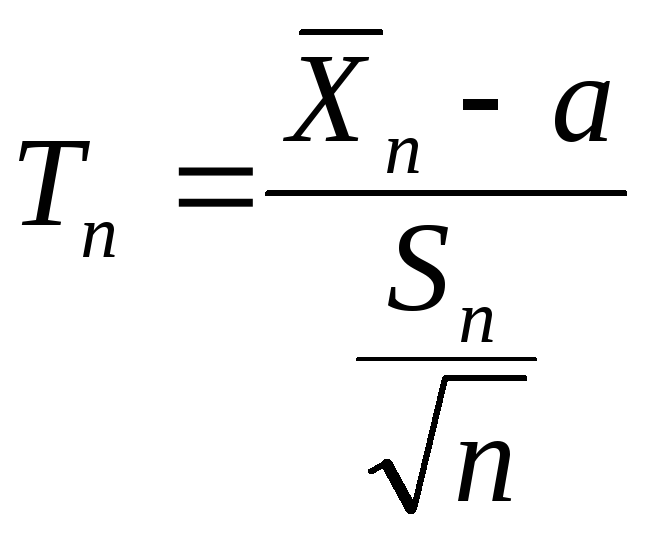
имеет известное распределение, не зависящее от параметров а и σ. Это распределение называется распределением Стьюдента, его плотность вероятности задается формулой

,

где коэффициент В_n определенным образом зависит от объема выборки n (конкретная формула не важна).

По заданной надежности γ найдем такое вспомогательное число t_γ, которое гарантировало бы выполнение условия P(|T_n|< t_γ) = γ . Посмотрим, к какому уравнению для t_γ приведет это условие. По общей формуле, выражающей вероятность попадания н.с.в. в заданный интервал , получаем: . Поэтому дляполучилось уравнение: 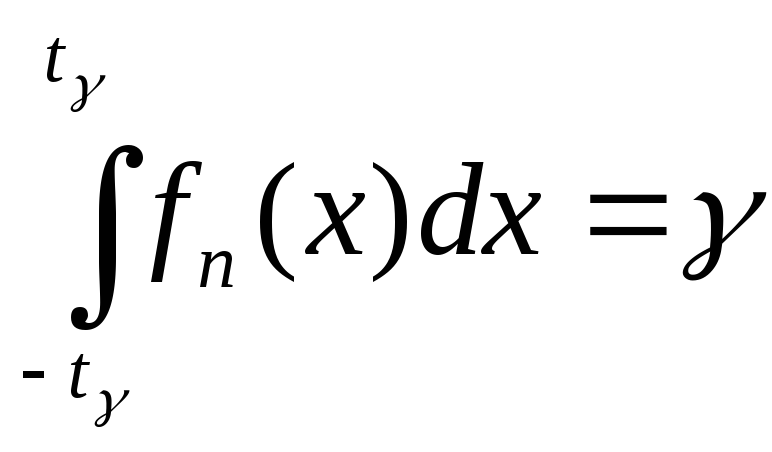. Конечно, это уравнение не решается аналитически, а только численно . Для различных значенийn и γ получены решения t_γ этого уравнения и результаты сведены в таблицу значений t_γ=t(γ,n). Тогда для этого значения t_γ выполнено следующее:

, т.е. .

Полученное равенство и означает, что доверительный интервал

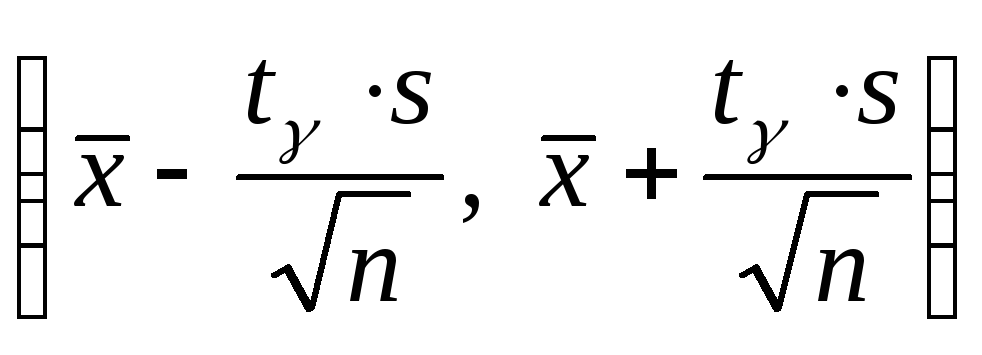
покрывает неизвестный параметр а с доверительной вероятностью γ , где − найденное выборочное среднее,s – исправленное среднее квадратическое отклонение, а значение параметра t_γ=t(γ,n) для различных значений n и γ приведено в специальных таблицах, связанных с распределением Стьюдента.

Пример. Некоторый признак Х генеральной совокупности распределен нормально. Для определения среднего значения признака Х была сделана выборка объема n=20, по которой вычислено выборочное среднее и выборочное исправленное среднее квадратическое отклонениеs = 0.4 . Найти , используя распределение Стьюдента, доверительный интервал для математического ожидания а признака Х с надежностью γ=0.99 .

Решение. Для надежности γ=0.99 и объема выборки n=20 по таблице значений t_γ=t(γ,n) находим t_γ=2.861. Тогда по выписанной выше формуле с вероятностью γ=0.99 среднее значение а признака Х заключено в интервале .

Пример. Некоторый признак Х генеральной совокупности распределен нормально. Для определения среднего значения признака Х была сделана выборка объема n=16, по которой вычислено выборочное среднее и выборочное исправленное среднее квадратическое отклонениеs = 0.8 . Найти доверительный интервал для математического ожидания а признака Х с надежностью γ=0.95 ( Ответ: 19.774 < a < 20.626 ).